Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Die Monde der Planeten
Dieses Kapitel ist ein Novum im Internet. Es ist der erste Abschnitt über die Berechnung der hellsten Planetenmonde. Herangezogen werden die Ephemeriden von J. Meeus für die Jupitermonde Io, Europa, Ganymed und Kallisto; und Dan Bruton für die Saturnmonde Tethys, Dione, Rhea, Titan und Japetus. Siehe auch die Literaturhinweise. Alle Monde haben synodische Umlaufszeiten.
Jupiter I
Diese Theorie setzt voraus, dass die Mondbahnen kreisförmig sind und mit dem Jupiteräquator zusammenfallen. Die Epoche ist 1900 Januar 0.5 und das Äquinoktium ist $J1900.0$.
$$d = JDE − 2415020.0$$
| Mond: | Radius | mittlere Länge |
|---|---|---|
| Io: | $r_1 = 5.906$ | $l_1 = 84\overset{\circ}{.}55061 + 203\overset{\circ}{.}405863 \cdot (d - \tau) + \varphi - C$ |
| Europa: | $r_2 = 9.397$ | $l_2 = 41\overset{\circ}{.}50155 + 101\overset{\circ}{.}291632 \cdot (d - \tau) + \varphi - C$ |
| Ganymed: | $r_3 = 14.989$ | $l_3 = 109\overset{\circ}{.}97702 + 50\overset{\circ}{.}2345169 \cdot (d - \tau) + \varphi - C$ |
| Kallisto: | $r_4 = 26.364$ | $l_4 = 176\overset{\circ}{.}35864 + 21\overset{\circ}{.}4879802 \cdot (d - \tau) + \varphi - C$ |
Jupiter II
in Arbeit …
Saturn I
Es wird ein Zusammenfallen aller kreisförmigen Mondbahnen (bis auf Japetus) mit dem Saturnäquator postuliert. Die Epoche ist 1980 Januar 0.5 und das Äquinoktium ist $J1980.0$.
$$d = JDE − 2444238.5$$
| Mond: | Radius | mittlere Länge |
|---|---|---|
| Tethys: | $r_1 = 4.8898$ | $l_1 = 172\overset{\circ}{.}8546 + 190\overset{\circ}{.}668614452\cdot (d - \tau) + \varphi - C$ |
| Dione: | $r_2 = 6.2637$ | $l_2 = 76\overset{\circ}{.}8438 + 131\overset{\circ}{.}505802072\cdot (d - \tau) + \varphi - C$ |
| Rhea: | $r_3 = 8.7476$ | $l_3 = 37\overset{\circ}{.}2555 + 79\overset{\circ}{.}6607672779\cdot (d - \tau) + \varphi - C$ |
| Titan: | $r_4 = 20.2695$ | $l_4 = 57\overset{\circ}{.}7005 + 22\overset{\circ}{.}54663941461\cdot (d - \tau) + \varphi - C$ |
| Japetus: | $r_5 = 59.0712$ | $l_5 = 195\overset{\circ}{.}3513 + 4\overset{\circ}{.}5045597067\cdot (d - \tau) + \varphi - C$ |
Spezialfall Japetus:
Die Neigung $\gamma$ der Japetusbahn zum Saturnäquator (Ringebene) ist gegeben mit:
| \[ \begin{align} \sin(\gamma) = &+\cos(\delta) \cdot \Big[\cos(83\overset{\circ}{.}51) \cdot \sin(40\overset{\circ}{.}27- \alpha) \cdot\\ &\cdot\sin(75\overset{\circ}{.}6)\sin(\alpha - 320\overset{\circ}{.}1) \cdot \cos(75\overset{\circ}{.}6) \cdot \sin(83\overset{\circ}{.}51)\Big]\\ &+\sin(\delta) \cdot \cos(83\overset{\circ}{.}51) \cdot \cos(75\overset{\circ}{.}6) \cdot \sin(320\overset{\circ}{.}1 - 40\overset{\circ}{.}27) \end{align} \] |
| \[\begin{align} \sin(V) =& - \cos(75\overset{\circ}{.}6)\cdot \cos(320\overset{\circ}{.}1- \alpha)\cdot \cos(\delta)\\ &- \sin(75\overset{\circ}{.}6)\cdot \sin(\delta) \end{align}\] |
| \[\tan(U) = \dfrac{\sin(\delta_0)\cdot \cos(\alpha_0 - \alpha) - \cos(\delta_0)\cdot \tan(\delta)} {\sin(\alpha_0 - \alpha)}\] |
mit den planetozentrisch planetoäquatorialen Koordinaten der Japetusbahn:
$$\alpha_0 = 318\overset{\circ}{.}16 − 3\overset{\circ}{.}949\cdot T$$ $$\delta_0 = 75\overset{\circ}{.}03 − 1\overset{\circ}{.}143\cdot T$$ und $$T = \frac{JDE - 2451545}{36525}$$
Bei $U$ ist auf die quadrantentreue Wiedergabe zu achten.
$V$ ist die planetozentrische Breite der Erde auf der Mondbahn.
$U$ ist die planetozentrische Länge der Erde auf der Mondbahn.
$\alpha$, $\delta$ = geozentrisch äquatoriale Koordinaten des Saturn.
Saturn II
in Arbeit …
Uranus
Das Postulat ist die Kreisförmigkeit der Mondbahnen und das die Monde in der Ringebene des Uranus liegen. Die Epoche ist 2000 Januar 1.5 und das Äquinoktium ist $J2000.0$. $$d = JDE − 2451545.0$$
| Mond: | Radius | mittlere Länge |
|---|---|---|
| Ariel: | $r_1 = 7.470$ | $l_1 = 203\overset{\circ}{.}08553309448 + 142\overset{\circ}{.}8356475830\cdot (d - \tau) + \varphi - C$ |
| Umbriel: | $r_2 = 10.407$ | $l_2 = 251\overset{\circ}{.}20712282177 + 86\overset{\circ}{.}8688659668\cdot (d - \tau) + \varphi - C$ |
| Titania: | $r_3 = 17.070$ | $l_3 = 281\overset{\circ}{.}54711908352 + 41\overset{\circ}{.}3514099121\cdot (d - \tau) + \varphi - C$ |
| Oberon: | $r_4 = 22.828$ | $l_4 = 352\overset{\circ}{.}56292444211 + 26\overset{\circ}{.}7394809723\cdot (d - \tau) + \varphi - C$ |
Neptun
Die Bahn von Triton wird als kreisförmig angenommen. Die Epoche ist 1950 Januar 1.0 und das Äquinoktium ist J1950,0.
$$d = JD − 2433282.5$$
| Mond: | Radius | mittlere Länge |
|---|---|---|
| Triton: | $r = 14.3196575674$ | \(\begin{align} l &= 49\overset{\circ}{.}85334766\\ &+ 61\overset{\circ}{.}25726751\cdot (d - \tau)\\ &+ \varphi - C \end{align}\) |
Bahnneigung Tritons (retrograde Bewegung): $\gamma = 157\overset{\circ}{.}6852321$
Legende
$C$ = Mittelpunktsgleichung (Mpgl.) des Hauptplaneten (siehe Abschnitt Mittelpunktsgleichung)
$\varphi$ = Phasenwinkel des Hauptplaneten (siehe Abschnitt Phasenwinkel)
$r$ = Bahnradien der Monde in Planetenradien
$l$ = Länge des Mondes mit Bezug auf die Sichtlinie Planet - Erde
$\tau$ = Lichtlaufzeit (siehe Abschnitt über die Lichlaufzeit)
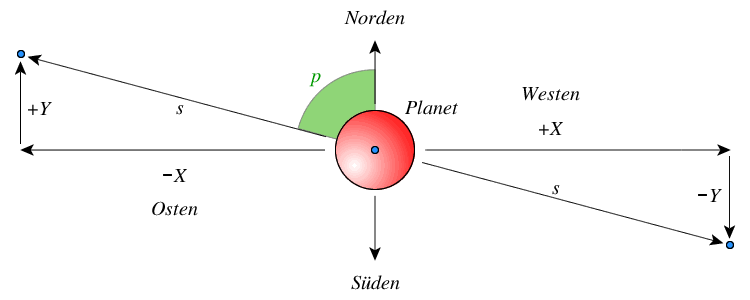
Darstellung der Monde am Himmel
Man berechne für alle Planetenmonde
\[ \begin{align} X_k &= + r_k \cdot \sin(l_k)\\ &= s \cdot \cos(p - 90^{\circ}) \\\\ Y_k &= - r_k \cdot \cos(l_k) \cdot \sin(D_E)\\ &= s \cdot \sin(p - 90^{\circ}) \end{align} \]
und zusätzlich für Japetus und Triton:
\[ \begin{align} X_j &= X_k \cdot \cos(\gamma) + Y_k \cdot \sin(\gamma)\\ &= s \cdot \cos(p - 90^{\circ}) \\\\ Y_j &= Y_k \cdot \cos(\gamma) - X_k \cdot \sin(\gamma)\\ &= s \cdot \sin(p - 90^{\circ}) \end{align} \]
Den Abstand $s$ und den Positionswinkel $p - 90^{\circ}$ erhält man im Abschnitt über die sphärische Darstellung.
$D_E$ = planetozentrische Deklination der Erde über der Äquatorebene des Planeten.
Helligkeit
Die absolute Helligkeit der natürlichen Satelliten aus $1\,AE$ Entfernung sind in der Tabelle angegeben.
| Planet | Name | Magnitude |
|---|---|---|
| Jupiter: | Io | $m_1 = - 1\overset{m}{.}68 + 4\overset{m}{.}60 \ (\frac{\varphi}{100^{\circ}}) - 10\overset{m}{.}0 \ (\frac{\varphi}{100^{\circ}})^2$ |
| Europa | $m_2 = - 1\overset{m}{.}41 + 3\overset{m}{.}12 \ (\frac{\varphi}{100^{\circ}}) - 12\overset{m}{.}5 \ (\frac{\varphi}{100^{\circ}})^2$ | |
| Ganymed | $m_3 = - 2\overset{m}{.}09 + 3\overset{m}{.}23 \ (\frac{\varphi}{100^{\circ}}) - 6\overset{m}{.}6 \ (\frac{\varphi}{100^{\circ}})^2$ | |
| Kallisto | $m_4 = - 1\overset{m}{.}05 - 7\overset{m}{.}80 \ (\frac{\varphi}{100^{\circ}}) - 27\overset{m}{.}4 \ (\frac{\varphi}{100^{\circ}})^2$ | |
| Saturn: | Tethys | $m_1 = + 0\overset{m}{.}60 + 2\overset{m}{.}00 \ (\frac{\varphi}{100^{\circ}})$ |
| Dione | $m_2 = + 0\overset{m}{.}80 + 2\overset{m}{.}29 \ (\frac{\varphi}{100^{\circ}})$ | |
| Rhea | $m_3 = + 0\overset{m}{.}10 + 2\overset{m}{.}40 \ (\frac{\varphi}{100^{\circ}})$ | |
| Titan | $m_4 = - 1\overset{m}{.}28 + 0\overset{m}{.}92 \ (\frac{\varphi}{100^{\circ}}) - 5\overset{m}{.}0 \ (\frac{\varphi}{100^{\circ}})^2$ | |
| Japetus: | $m_5 = + 1\overset{m}{.}48 - 2\overset{m}{.}5 \ \log_{10}(H)$ | |
| Uranus: | Ariel | $m_1 = + 1\overset{m}{.}45$ |
| Umbriel | $m_2 = + 2\overset{m}{.}10$ | |
| Titania | $m_3 = + 1\overset{m}{.}02$ | |
| Oberon | $m_4 = + 1\overset{m}{.}23$ | |
| Neptun: | Triton | $m_5 = - 1\overset{m}{.}24$ |
mit
| $$H = 0\overset{m}{.}571 - 0\overset{m}{.}429\cdot\sin\big[\arcsin\big(\cos(V)\cdot\cos(l_5 - U)\big)\big]$$ |
Die scheinbare Helligkeit der Planetenmonde berechnet sich mit der Formel aus dem Abschnitt über die Helligkeit der Planeten. Die Gleichungen stammen aus dem Explanatory Supplement.
- Die Phasenwinkelabhängigkeit der Jupitermonde stammen von C. Blanco & S. Catalano und aus dem Explanatory Supplement.
- Weil Japetus eine gebundene Rotation hat und eine unterschiedliche Oberfläche mit verschiedenen Albedos aufweist, ist er in seiner westlichen Elongation um die zwei Magnituden heller als in der östlichen. Die Magnituden schwanken deshalb zwischen $10\overset{m}{.}1$ und $12\overset{m}{.}9$. Die Gleichung für $H$ stammt von D.L. Harris und D. Morrison.
- Die Phasenwinkelabhängigkeit Titans stammt von C. Blanco & S. Catalano.
- Die Phasenkoeffizienten für Tethys und Dione stammen von D. Morrison & D.P. Cruikshank, L.K. Kristensen und von C. Blanco & S. Catalano.
- Für Rhea wurde der Phasenkoeffizient von B.J. Buratti, J.A. Mosher et al. entnommen.
- Für Uranus und Neptun sind keine Phasenterme bekannt.