Stern- und Planetenbedeckungen haben den Vorteil, dass sich der Mond nicht in Sonnen- oder Erdschattennähe aufhalten muss, obwohl dieses reizvoll zu beobachtende Phänomen von der geographischen Position abhängig ist.

Zu Beginn benötigt man die Positionen der Sterne, die man aus unzähligen Katalogen wie z.B. den PPM (Position and Proper Motion Katalog), den SAO Katalog (Smithonian Astrophysical Observatory), sowie der Uranometria 2000,0 entnehmen kann. Die Kataloge haben ein Äquinoktium, sowie eine Rubrik der Eigenbewegungen $\mu_{\alpha}$ und $\mu_{\delta}$ der Sterne mit $t_0$ als der Katalogepoche und t als den gesuchten Zeitpunkt.

\[\begin{align} \alpha\left(t\right) &= \alpha_0 + \mu_\alpha \left(t - t_0\right) \quad\textsf{und} \\ \delta\left(t\right) &= \delta_0 + \mu_\delta \left(t - t_0\right) \end{align}\tag{1}\]

Ist die Eigenbewegung berücksichtigt, so muss die Aberration, die Präzession, die Nutation und die Refraktion angebracht werden. Man bekommt die scheinbaren Koordinaten $\alpha_*$ und $\delta_*$.

Der Mond hat die beiden Kontaktzeitpunkte $t_1$ und $t_2$ (Zeitintervall [$t_1$, $t_2$]) und die entsprechenden die Rektaszensionen $\alpha_M(t_1)$ und $\alpha_M(t_2)$. Durch den Vergleich der Deklinationen $\delta_M$ des Mondes mit $\delta_*$ des Sterns und einem Vorzeichenwechsel von $\Delta\alpha (t)$ bekommt man einen ersten Hinweis auf eine Konjunktion (noch keine Sternbedeckung!).

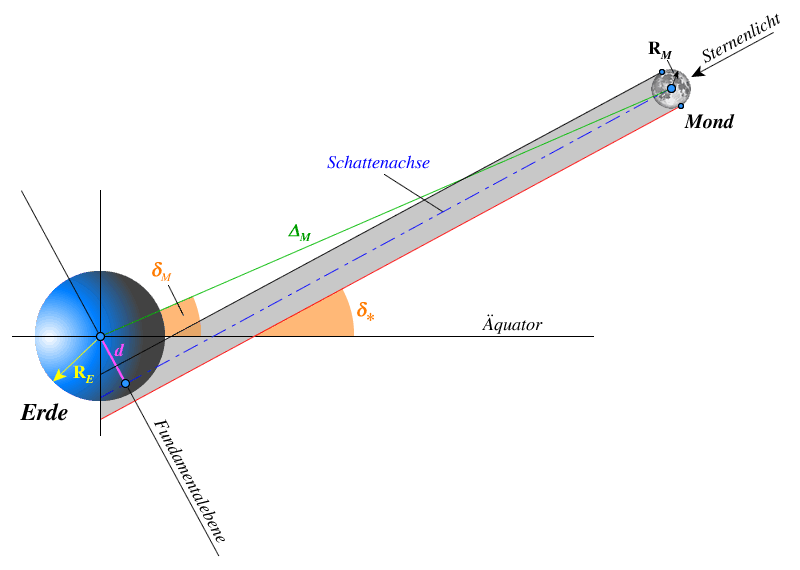Abb. 1: Sternbedeckung durch den Mond

Die Konjunktionszeit $t_c$ des Sterns mit dem Mond ermittelt man wieder mit der Regula Falsi und dem Pegasus-Verfahren:

\[\begin{align} t_c &= t_2 - \Delta\alpha_2\cdot \frac{t_2 - t_1}{\Delta\alpha_2 - \Delta\alpha_1}\\ &\textsf{mit}\quad \Delta\alpha_i = \alpha_M\left(t_i\right) - \alpha_* \end{align}\tag{2}\]

• Ist $\alpha_M(t_c) \gt \alpha_*$ ersetzt man $t_1$ durch $t_c$
• Ist $\alpha_M(t_c) \lt \alpha_*$ ersetzt man $t_2$ durch $t_c$.
  Es gilt dann wieder $\alpha_M(t_1) \lt \alpha_* \lt \alpha_M(t_2)$.
• Wenn $\Delta\alpha_c\cdot \Delta\alpha_2 \le 0$
  → ersetze $t_1,\Delta\alpha_1$ durch $t_2,\Delta\alpha_2$
• Wenn $\Delta\alpha_c\cdot \Delta\alpha_2 \gt 0$
  → ersetze $t_1,\Delta\alpha_1$ durch $t_1,\frac{\Delta\alpha_1\cdot\Delta\alpha_2}{\Delta\alpha_1 + \Delta\alpha_c}$

In beiden Fällen wird $t_2$, $\Delta\alpha_2$ durch $t_c$, $\Delta\alpha_c$ ausgetauscht.

Die Bedingung für eine Sternbedeckung ist der Abstand $d$ der Schattenachse zum Erdmittelpunkt: $$d < R_E + R_M \approx 1,5 R_E \quad\text{und}\quad d = \Delta_M \ |\sin(\delta_M - \delta_*)| = |\vec{r}_M - (\vec{e}_*\cdot\vec{r}_M) \vec{e}_*| < 1,5 \ R_E\tag{3}$$

Ausserhalb von $1.5$ Erdradien findet keine Bedeckung statt.

$\vec{r}_M$ = $\vec{r}_M \left(\alpha_M, \delta_M, \Delta_M \right)$ sind die geozentrisch-äquatorialen Mondkoordinaten.
Die Mondkoordinaten im Bezugssystem der Fundamentalebene sind dann \[\left(\begin{aligned} & \cos(d_M)\cdot \cos(a_M) \\ & \cos(d_M)\cdot \sin(a_M) \\ & \sin(d_M) \end{aligned}\right) = \left(\begin{aligned} x_M \\ y_M \\ z_M \end{aligned}\right) = \left(\begin{aligned} & + \cos(\delta_M)\cdot \sin(\alpha_M - \alpha_*) \\ & - \cos(\delta_M)\cdot \cos\big(\alpha_M - \alpha_*\big)\cdot \sin(\delta_*) + \sin(\delta_M)\cdot \cos(\delta_*) \\ & + \cos(\delta_M)\cdot \cos\big(\alpha_M - \alpha_*\big)\cdot \cos(\delta_*) + \sin(\delta_M)\cdot \sin(\delta_*) \end{aligned}\right)\tag{4}\]

Ebenso wird die geographische Position $\lambda_0$, $\beta_0$ des Beobachters $\vec{e}_G \big(\lambda_0, \beta_0\big)$ mit der Sternzeit $\theta_0$ gebraucht.

\[\left( \begin{aligned} & \cos(d_G)\cdot \cos(a_G) \\ & \cos(d_G)\cdot \sin(a_G) \\ & \sin(d_G) \end{aligned} \right) = \left( \begin{aligned} x_G \\ y_G \\ z_G \end{aligned} \right) = \left( \begin{aligned} & \cos(\beta_0)\cdot \cos\big(\theta + \lambda_0\big) \\ & \cos(\beta_0)\cdot \sin\big(\theta + \lambda_0\big) \\ & \sin(\beta_0) \end{aligned} \right)\tag{5}\]

Der Verlauf der Sternbedeckung hängt von den Differenzen $f = x_M - x_G$ und $g = y_M - y_G$ ab. Ist der Abstand $h = \sqrt{f^2 + g^2}$ des Beobachters von der Mondschattenmitte (des Sterns auf der Erdoberfläche) kleiner als der Mondradius $R_M$, so findet eine Sternbedeckung am Ort des Beobachters statt. Die Ein- und Austrittszeit berechnet man mit: $$s(t) = f(t)^2 + g(t)^2 - R_M^2\tag{6}$$

$s(t)$ wird $2.5$ Stunden vor und nach der Bedeckung viertelstündlich neu berechnet. Daraus werden die beiden Nullstellen t$_0$ der Gleichung ermittelt. Man kann in erster Näherung $t_c$ zur viertelstündlichen Berechnung nehmen.

Der Positionswinkel P gibt den Ein- und Austrittsrichtung des Sterns hinter dem Mond an. Die Zählrichtung ist von Norden nach Osten gegen den Uhrzeigersinn. \[\left(\begin{aligned} \cos(P) \\ \sin(P) \end{aligned}\right) = - \frac{1}{h} \left(\begin{aligned} g \\ f \end{aligned} \right)\tag{7}\]

Die Sternbedeckungen werden von Sternwarten und Observatorien mit den geographischen Koordinaten $\lambda_{st}$, $\beta_{st}$ herausgegeben. Mit der Gleichung $$t = a\cdot (\lambda_0 - \lambda_{st}) + b\cdot (\beta_0 - \beta_{st})\tag{8}$$

kann man diese auf die geographischen Koordinaten $\lambda_0$, $\beta_0$ des Beobachters umgerechnet werden. $a$ und $b$ sind die sogenannten Stationskoeffizienten von den eben genannten Instituten. Eine Sternbedeckung wird ferner zu einer ersten Abschätzung der Differenz zur Ephemeridenzeit $\Delta T$ benutzt: $$\Delta T = \frac{s(t) - t_{ut}}{1 + a\cdot 0.25^{\circ/m}}\tag{9}$$

$s(t)$ ist der berechnete und $t_{ut}$ der beobachtete Bedeckungszeitpunkt.

Der Mond bedeckt hin und wieder auch die Planeten. Die Gleichungen sind für die Planetenbedeckungen die gleichen wie bei den Sternbedeckungen, nur die Ausdehnung des Planetenscheibchens (Venusphasen, Saturnringe und Jupiterabplattung!) ist zu berücksichtigen. Das Phänomen der Planetenbedeckung entspricht einer Sonnenfinsternis, deshalb ist auch analog zur Sonnenfinsternis vorzugehen. Die Kontaktdauer ist dann $\tau$ (Handbuch für Sternfreunde)

$$\tau = \varnothing \cdot \vert (\alpha_M - \alpha_P) \cdot \sin(P) - (\delta_M - \delta_P) \ \cos(P) \vert\tag{10}$$

mit den Koordinaten des Mondes (Index $M$) und der Planeten (Index $P$).

Das Phänomen der Sternbedeckung durch die Planeten berechnet sich wie eine Sternbedeckung durch den Mond. Man ersetzt die Koordinaten des Erdmondes $\vec{r}_M \big(\alpha_M, \delta_M, \Delta_M\big)$ gegen die des Planeten $\vec{r}_P\big(\alpha_P, \delta_P, \Delta_P\big)$. Als Bedingung für eine planetare Sternbedeckung kann der folgende Ausdruck Auskunft geben (Explanatory Supplement):

$$\vert\delta_P - \delta_*\vert \lt \frac{\pi_P + \frac{\varnothing}{2}} {\vert\sin(P)\vert}\tag{11}$$

$P$ ist der Positionswinkel der Bewegungsrichtung des Planeten und $\pi_P$ die entsprechende Parallaxe.