In diesem Kapitel werden die geozentrisch ekliptikalen Koordinaten des Mondes berechnet und dabei zwei Theorien gegenüber gestellt:

• ILE (Brownsche Mondtheorie), entnommen aus Astronomie mit dem Personal Computer (O. Montenbruck & T. Pfleger)
• ELP2000 (Chaprontsche Theorie), entnommen aus Astronomical Algorithms (J. Meeus)

in niedriger, aber für die meisten Zwecke ausreichender Genauigkeit. Es gilt für $T$ die Epoche $J1900.0$.

$$\label{epoch} T = \frac{JDE - 2415020.0}{36525}\tag{1}$$

In der Länge $\lambda$ fallen beide Theorien in den Störtermen zusammen:

$$\begin{align} \Delta\lambda = & +22640'' \cdot \sin(m)\\ &+769'' \cdot \sin(2 m) \\ &+36'' \cdot \sin(3 m) \\ &+4587'' \cdot \sin(2 D - m)\\ &+2370'' \cdot \sin(2 D) \\ &-668'' \cdot \sin(M) \\ &-412'' \cdot \sin(2 F) \\ &+212'' \cdot \sin(2 \cdot (D - m)) \\ &+206'' \cdot \sin(2 D - M - m)\\ &+192'' \cdot \sin(2 D + m)\\ &+165'' \cdot \sin(2 D - M)\\ &+148'' \cdot \sin(m - M) \\ &-125'' \cdot \sin(D) \\ &-110'' \cdot \sin(m + M)\\ &+55'' \cdot \sin(2 \cdot (D - F))\\ &-45'' \cdot \sin(2 F + m)\\ &-40'' \cdot \sin(2 F - m)\\ &+38'' \cdot \sin(4 D - m) \end{align}\tag{2}$$

In der Breite $\beta$ gehört $\Delta\beta_1$ zur ILE und $\Delta\beta_2$ zur ELP2000. Die Brownsche Mondtheorie benötigt vorab noch einen Hilfsterm:

$$\begin{align} \Delta G =&\; \frac{1}{3600''}\cdot \big[\Delta\lambda\\ &+412''\cdot \sin(2\cdot F)\\ &+541''\cdot \sin(M)\big] \end{align}\tag{3}$$

Störterme in der Breite für die DE200: $$\begin{align} \Delta\beta_1 = & +18520'' \cdot \sin(F + \Delta G)\\ &-526'' \cdot \sin(F - 2 D)\\ &+44'' \cdot \sin(F - 2 D + m)\\ &-31'' \cdot \sin(F - 2 D - m)\\ &-23'' \cdot \sin(F - 2 D + M)\\ &+11'' \cdot \sin(F - 2 D - M)\\ &-25'' \cdot \sin(F - 2 m)\\ &+21'' \cdot \sin(F - m)\\ &+24'' \cdot \sin(F + M)\\ &-14'' \cdot \sin(m) \end{align}\tag{4}$$

Störterme in der Breite für die ELP2000: $$\begin{align} \Delta\beta_2 = & +18462'' \cdot \sin(F)\\ &+1010'' \cdot \sin(m + F)\\ &+1000'' \cdot \sin(m - F)\\ &+624'' \cdot \sin(2 D - F)\\ &+200'' \cdot \sin(2 D + F - m)\\ &+167'' \cdot \sin(2 D - F - m)\\ &+117'' \cdot \sin(2 D + F)\\ &+62'' \cdot \sin(2 m + F)\\ &+33'' \cdot \sin(2 D - F + m )\\ &+32'' \cdot \sin(2 m - F) \end{align}\tag{5}$$

Auch bei der Parallaxe fallen beide Theorien in dieser Größenordnung zusammen: $$\begin{align} \Delta\Pi = & +187'' \cdot \cos(m)\\ &+10'' \cdot \cos(2 m)\\ &+34'' \cdot \cos(2 D - m)\\ &+28'' \cdot\cos(2 D)\\ &+3'' \cdot \cos(2 D + m) \end{align}\tag{6}$$

Die Parallaxe ist der vom Mond aus gesehene Erdhalbmesser.

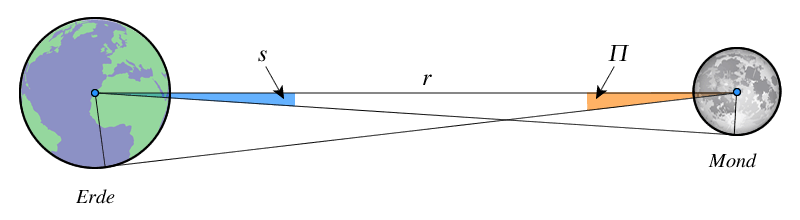Abb. 1: Parallaxe und Erdhalbmesser

Es fehlt nur noch der Störungsterm für den Radius $r$:

$$\begin{align} \Delta r = & -20905\,\mathrm{km} \cdot\cos(m\\ &-570\,\mathrm{km} \cdot \cos(2 m)\\ &-3699\,\mathrm{km} \cdot \cos(2 D - m)\\ &-2956\,\mathrm{km} \cdot\cos(2 D)\\ &+246\,\mathrm{km} \cdot \cos(2 (m - D))\\ &-205\,\mathrm{km} \cdot \cos(M - 2 D)\\ &-171\,\mathrm{km} \cdot\cos(m + 2 D)\\ &-152\,\mathrm{km} \cdot \cos(m + M - 2 D) \end{align}\tag{7}$$

Auch beim Radius $r$ fallen beide Theorien zusammen. Damit hat man die geozentrisch ekliptikalen Koordinaten des Mondes vorliegen:

Der Index $k = 1, 2$ bezeichnet die jeweilige Theorie.

Die beiden ausführlichen Theorien mit deutlich höherer Genauigkeit haben aufgrund ihres großen Umfangs zwei Extraseiten erhalten. Sie sind hier zu finden:

• J. Meeus und
• Montenbruck/Pfleger

Ferner gibt es einen Vergleich dieser beiden Theorien.

Der geozentrische Durchmesser des Mondes lautet:

$$\begin{align} &\sin\left(\frac{\varnothing}{2}\right) = 0.2724934056\cdot \sin(\Pi)\\ &\textrm{mit}\quad\dfrac{R_M}{R_E} = 0.2724934056 \end{align}\tag{8}$$

Und den topozentrischen Durchmesser ermittelt man mit: $$\tan\left(\frac{\varnothing}{2}\right) = \frac{R_M}{\Delta'}\tag{9}$$

$\Delta'$ ist der topozentrische Abstand. Die Ausgabe ist in Grad und sollte ggf. durch Multiplikation mit $60$ in Bogenminuten umgerechnet werden.

Der Sonnenpositionswinkel $\theta$ und die Elongation $\eta$ werden in diesem Abschnitt berechnet. $\alpha_0$, $\delta_0$ müssen die Koordinaten der Sonne und $\alpha$, $\delta$ die Koordinaten des Mondes sein. Ist die Elongation bekannt, so kann mit guter Genauigkeit (J. Meeus) die Relation für den Phasenwinkel $\varphi$ gelten: $$\cos(\varphi) = -\cos(\eta)\tag{10}$$

Dies ist möglich, weil $\sigma \ll 1$ gilt. Der Beleuchtungsgrad $k$ ist dann:

$$k = \frac{1}{2} \cdot \big(1 + \cos (\varphi)\big) \cdot 100\%\tag{11}$$

Nach J. Meeus Astronomical Algorithms kann man den Phasenwinkel $\varphi$ genähert mit der folgenden Beziehung berechnen:
Man berechnet die Delauney-Argumente $D, M$ und $m$ mit

$$\begin{align} D &=\,297\overset{\circ}{.}8501921\\ &+445267\overset{\circ}{.}1114034\cdot T\\ &-0\overset{\circ}{.}0018819\cdot T^2 \end{align}\tag{12}$$

$$\begin{align} M &=\,357\overset{\circ}{.}5291092\\ &+35999\overset{\circ}{.}0502909\cdot T\\ &-0\overset{\circ}{.}0001536\cdot T^2 \end{align}\tag{13}$$

$$\begin{align} m &=\,134\overset{\circ}{.}9633964\\ &+477198\overset{\circ}{.}8675055\cdot T\\ &+0\overset{\circ}{.}0087414\cdot T^2 \end{align}\tag{14}$$

Es genügt hier, nur Terme bis zur 2. Potenz in $T$ zu berücksichtigen. $T$ sind wieder die julianischen Jahrhunderte bezüglich der Epoche $J2000$, nämlich

$$T = \frac{JD - 2451545.0}{36525}\tag{15}$$

Daraus erhält man einen guten Näherungswert für den Phasenwinkel mit $$\begin{align} \varphi &=\,180^{\circ} - D\\ &-6\overset{\circ}{.}289\cdot\sin(m)\\ &+2\overset{\circ}{.}100\cdot\sin(M)\\ &-1\overset{\circ}{.}274\cdot\sin(2\cdot D - m)\\ &-0\overset{\circ}{.}658\cdot\sin(2\cdot D)\\ &-0\overset{\circ}{.}214\cdot\sin(2\cdot m)\\ &-0\overset{\circ}{.}110\cdot\sin(D) \end{align}\tag{16}$$

Mit Hilfe des Phasenwinkels $\varphi$ ist es nun möglich, die Helligkeit $H$ des Mondes am Firmament zu berechnen:

$$\begin{align} H = -12\overset{m}{.}74 &+ 5\cdot \log_{10}(R\cdot\Delta) \\ &+ 2\overset{m}{.}825\cdot \left(\frac{\varphi}{100}\right) \\ &-0\overset{m}{.}51\cdot \left(\frac{\varphi}{100}\right)^2 \\ &+ 0\overset{m}{.}525\cdot \left(\frac{\varphi}{100}\right)^3 \\ &+ 0\overset{m}{.}2\cdot \left(\frac{\varphi}{100}\right)^4 \\ \end{align}\tag{17}$$

$\Delta$ ist die geozentrische Monddistanz und $R$ der heliozentrische Erdabstand. Beide Variablen sind in AE gehalten: $a$ ist die große Halbachse des Mondes mit $a = 383397.7725$ km. Diese muss in $AE$ (⇒ Wichtige Konstanten) umgerechnet werden.

$$a = \frac{383397.7725\,km}{149597870.7\tfrac{km}{AE}} = 0.002562855813\,AE\tag{18}$$

Die Helligkeit des Erdtrabanten ist ein Mittelwert aus den Gleichungen, die in D.L. Harris (Photometry and Colormetry of Planets and Satellites) und im C.W. Allen (Astrophysical Quantities) zu finden sind.

Der Mond hat eine gebundene Rotation, d.h., er zeigt uns immer dieselbe Seite. Dennoch gibt es Rotationselemente für unseren Erdtrabanten. $T$ und $d = JD - 2451545$ beziehen sich dabei auf die Epoche $J2000.0$. Siehe auch den Abschnitt über den Julianischer Tag JD.

$\alpha_0$, $\delta_0$ sind wieder die äquatorialen Pole und $W$ ist der Nullmeridian des Erdtrabanten. Im Kapitel über die planetozentrischen Koordinaten können durch Einsetzen die selenozentrischen Koordinaten $A$, $D$ und den Positionswinkel $P$ der Rotationsachse des Mondes ermittelt werden. Die Libration ist dabei schon enthalten.

Die Rotationselemente des Erdtrabanten stammen aus dem Report der IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites.

Die Libration besteht aus drei Phänomenen, die hier kurz abgehandelt werden.

Abb. 2: Optische Libration

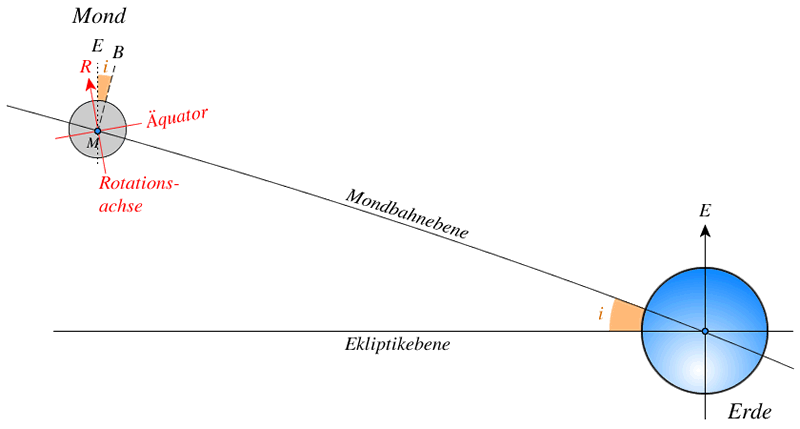
Die Rotationsachse des Mondes, die Achse der Ekliptik (also die Senkrechte zu dieser Ebene) und die Achse der Mondbahn (die Senkrechte zu seiner Ebene) liegen immer in derselben Ebene. Der Schnittpunkt der Äquatorialebene des Mondglobus mit der Ekliptik verläuft parallel zur Knotenlinie der Mondbahn. Der absteigende Knoten des Mondäquators fällt mit dem aufsteigenden Knoten der Umlaufbahn zusammen. Die Rotationsachse des Mondes ist zur Mondbahnebene derart geneigt, dass seine Pole temporär sichtbar werden. Dieses Phänomen wird als die optische Libration oder Libration in der selenographischen Breite genannt. Die Periode dieser Libration ist der drakonitische Monat.

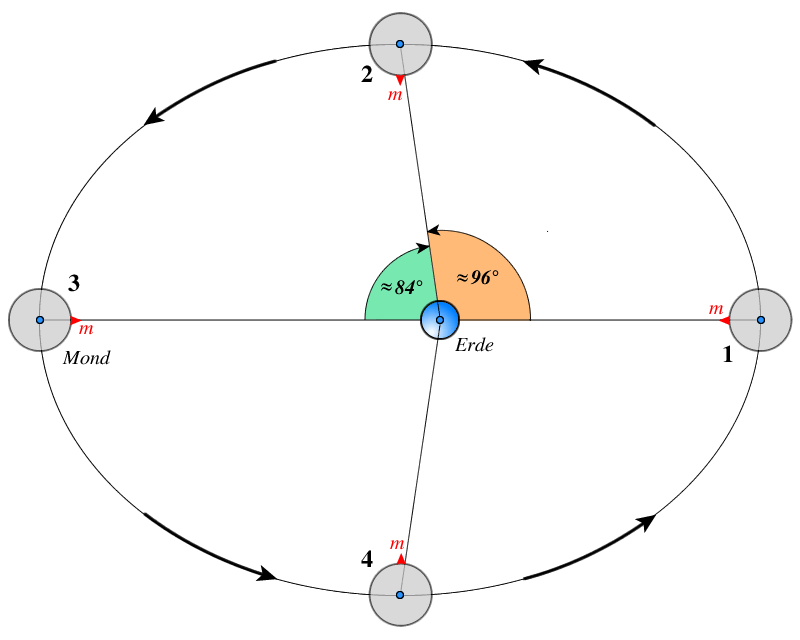Abb. 3: Physikalische Libration

Diese Drehung entsteht vor allem durch die leicht elliptische Umlaufbahn des Mondes. Für die Libration ist die große Ungleichheit verantwortlich. Dieses Phänomen wird als die physikalische Libration oder Libration in der selenographischen Länge genannt. Die Periode dieser Libration ist der anomalistische Monat.

Diese Libration ergibt sich aus der Tatsache, dass sich die Mondkugel gleichmäßig dreht (konstante Winkelgeschwindigkeit), während die Geschwindigkeit des Mondes auf seiner Umlaufbahn um die Erde variabel ist. In der Nähe des Perigäums, wo der Abstand zur Erde am geringsten ist, ist die Umlaufgeschwindigkeit größer als in der Nähe des Apogäums, wo der Abstand zur Erde maximal ist.

Abb.3 zeigt die Bewegung des Mondes um die Erde. Die Durchmesser von Erde und Mond sowie die Abstände sind natürlich nicht maßstabsgetreu. In Position 1 befindet sich der Mond im Perigäum. Sei $m$ zu diesem Zeitpunkt der Mittelpunkt der Mondscheibe (von der Erde aus gesehen). Man kann sich vorstellen, dass sich am Punkt $m$ ein großer Mondberg befindet, der auf die Erde gerichtet ist. Nach einer Viertelumdrehung (das sind ca. $\frac{27\overset{d}{.}32}{4} = 6\overset{d}{.}83$ Tage) hat sich die Mondkugel um genau $90^{\circ}$ gedreht. Der Mond hat dann Position 2 erreicht. Diese Position ist nicht genau bei $90^{\circ}$, sondern etwa bei $96^{\circ}$ Grad weiter in der Umlaufbahn als Position 1, und Punkt $m$ scheint nun nach Osten (nach „links“) verschoben zu sein. Am westlichen Mondrand sieht man etwas über den Rand der „mittleren“ sichtbaren Mondhälfte hinaus.

Eine halbe Umdrehung nach dem Perigäum erreicht der Mond sein Apogäum und hat von der Erde aus gesehen über $180^{\circ}$ zurückgelegt (Position 3). Auch die Mondkugel hat sich nun um $180^{\circ}$ gedreht und der Punkt $m$ liegt somit von der Erde aus gesehen wieder genau im Zentrum der Mondscheibe.

Eine Viertelumdrehung nach dem Apogäum hat sich Punkt $m$ um weitere $90^{\circ}$ in Bezug auf die Achse der Mondkugel gedreht. Aber der Mond hat sich nur über ca. $84^{\circ}$ in Bezug auf die Erde bewegt, weil die Geschwindigkeit in diesem Teil seiner Umlaufbahn geringer ist als sein Mittelwert. Der Mond befindet sich jetzt in Position 4 und man sieht etwas über den mittleren östlichen Rand seiner Scheibe hinaus; Punkt $m$ ist nun etwas westlich („rechts“) der Scheibenmitte zu sehen.

Nach einer weiteren Viertelumdrehung ist der Mond mit erhöhter Geschwindigkeit ins Perigäum zurückgekehrt und befindet sich, vom Erdpunktmittelpunkt aus gesehen, wieder genau im Zentrum der sichtbaren Hälfte der Mondkugel. Der zuvor genannte Winkel von $96^{\circ}$ ist ein Mittelwert: Tatsächlich kann dieser Winkel zwischen $95^{\circ}$ und $98^{\circ}$ variieren, da der Mond neben seiner elliptischen Umlaufbahn auch durch die Anziehungskraft der Sonne gestört wird.

Abb. 4: Topozentrische Libration

Die topozentrische Libration (auch tägliche oder parallaktische Libration genannt) entsteht zum Einen durch den unterschiedlichen Beobachtungsort (z.B. Nord- oder Südhalbkugel) und zum Anderen durch die Erdrotation. Ein Beobachter $B$ sieht den Mond bei Mondaufgang von einer etwas anderen Position als beim Monduntergang.

Der Berechnung der Libration ist ein eigenes Kapitel gewidmet.

Das Mondalter $MA$ bezeichnet die Anzahl der Tage seit dem letzten Neumond.

$$MA = \mathrm{red}(l − L,360^{\circ})\tag{19}$$

mit der Reduktionsfunktion red(x;y). Die Berechnung stammt aus K. Hempe & J. Molt.

Die Korrektur für die Perigäumspassage wird zum julianischen Tag dazuaddiert:

$$\begin{align} \Delta JDE_\pi &= 6793\overset{d}{.}476501\\ &+ 1\overset{d}{.}24002\cdot 10^{-4}\cdot T\\ &+ 2\overset{d}{.}2325\cdot 10^{-9}\cdot T^2\\ &- 1\overset{d}{.}3985\cdot 10^{-13}\cdot T^3 \end{align}\tag{20}$$

Die Korrektur für den Knotendurchgang wird zum julianischen Tag dazuaddiert:

$$\begin{align} \Delta JDE_\Omega &= 3232\overset{d}{.}60542496\\ &+ 1\overset{d}{.}68939\cdot 10^{-4}\cdot T\\ &+ 2\overset{d}{.}9833\cdot 10^{-9}\cdot T^2\\ &- 1\overset{d}{.}8809\cdot 10^{-13}\cdot T^3 \end{align}\tag{21}$$

$T$ ist wieder in Jahrhunderten der Epoche $J2000.0$. $\Delta JDE_{\pi,\Omega}$ muss nur noch zum aktuellen $JD$ hinzuaddiert werden. Die beiden Ausdrücke stammen von Viktor Reijs.

Für eine ausführliche Darstellung wird auf ein eigenes Kapitel verwiesen.

Dem Thema Mondphasen ist ein eigenes Kapitel gewidmet. Es geht um die Berechnung der Zeitpunkte von Vollmond, Neumond etc. Dies ist auch für die Finsternisse essentiell.