Inhaltsverzeichnis
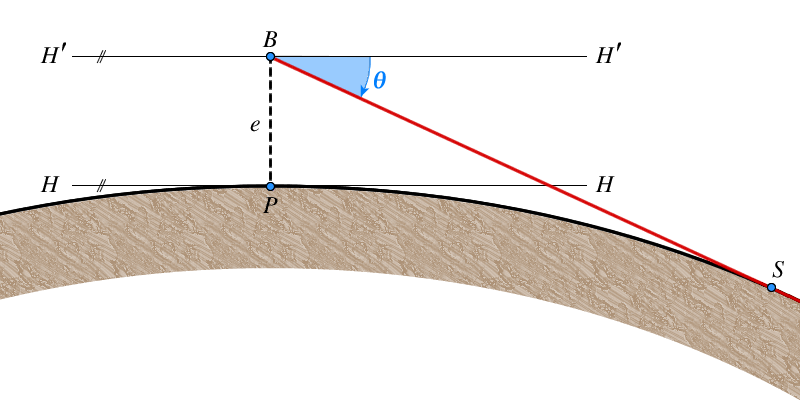
Sichtweite und Kimmtiefe
Dieses Thema kommt eher aus der Nautik, Meteorologie oder Geodäsie als aus der Ephemeridenrechnung. Es geht um die (berechenbare) Entfernung zum Horizont (Sichtweite) und den dazugehörenden Winkel. Die Kimmtiefe ist der Winkel, den die Horizontale vom Auge des um e erhöhten Beobachters (der „wahre“, astronomische Horizont) mit der Tangente an die Erdoberfläche (der sichtbare Horizont) bildet. Im Folgenden wird der Effekt der atmosphärischen Lichtbrechung vernachlässigt. Es gibt aber Möglichkeiten, die Lichtbrechung bei diesem Thema ebenfalls zu berücksichtigen.
In der Abb.1 ist $\overline{HH}$ (bzw. $\overline{H'H'}$) der astronomische Horizont und $\overline{BS}$ der sichtbare Horizont des Beobachters $B$, der sich in einer Höhe $e = \overline{PB}$ über der Erdoberfläche befindet.
Den Winkel $\theta$ nennt man in der Nautik Kimmtiefe (engl. Dip). Aufgrund der Erdkrümmung kann der Beobachter oberhalb der Erdoberfläche unter den astronomischen Horizont blicken. Die Kimmtiefe $\theta$ hängt von der Höhe des $e$ Beobachters ab.
In der Abb.2 sei $M$ der Erdmittelpunkt, $h$ die Sichtweite $\overline{BS}$ und $r = \overline{MP} = \overline{MS}$ der Radius der Erde. Im rechtwinkligen Dreieck $\triangle MBS$ haben wir
\[\begin{align} r^2 + h^2 &= (r + e)^2\\ h &= \sqrt{(r + e)^2 - r^2} = \sqrt{2\cdot e\cdot r + e^2}\\ h &\approx \sqrt{2\cdot e\cdot r} \end{align}\]
da $e^2$ eine sehr kleine Größe ist. Da $\theta$ ein kleiner Winkel ist, gilt im Bogenmaß $\theta\approx\tan\theta$, woraus
$$\theta^{rad}\approx \tan\theta = \frac{h}{r}\approx \sqrt{\frac{2\cdot e}{r}}$$
folgt. Nimmt man für $r$ einen Mittelwert (von Äquator- und Polradius) von $6367.45\;km = 6367450\;m$ an und rechnet Radiant in Grad um, ergibt sich die Näherungsformel
\[\begin{align} \theta^{\circ} &\approx \frac{180^{\circ}}{\pi} \cdot \sqrt{\frac{2}{r}} \cdot \sqrt{e}\\ \theta^{\circ} &\approx \frac{180^{\circ}}{\pi} \cdot \sqrt{\frac{2}{6367450}} \cdot \sqrt{e}\\ \theta^{\circ} &\approx 0.032111 \cdot \sqrt{e} \end{align}\tag{1}\]
wobei $e$ in Metern ausgedrückt wird.
Für einige Werte der Höhe $e$ des Beobachters gibt die nachstehende Tabelle 1 den entsprechenden Wert $\theta$ an. Man stellt fest, dass bei einer Höhe von nur einem Meter die Kimmtiefe bereits $2''$ beträgt! Bei größeren Höhen nimmt die Kimmtiefe jedoch immer langsamer zu. Um eine 10mal so große Kimmtiefe zu erhalten, muss die Höhe mit 100 multipliziert werden. Bei einer Höhe von etwa 276 Metern entspricht die Kimmtiefe etwa dem scheinbaren Winkeldurchmesser der Sonne.
| Tabelle 1 | ||
|---|---|---|
| Höhe von $B$ in $[m]$ | $\theta$ | Sichtweite in $[km]$ |
| $0$ | $0^{\circ}$ | $0$ |
| $1$ | $0^{\circ}01'56''$ | $4$ |
| $2$ | $0^{\circ}02'43''$ | $5$ |
| $10$ | $0^{\circ}06'06''$ | $11$ |
| $50$ | $0^{\circ}13'37''$ | $25$ |
| $100$ | $0^{\circ}19'16''$ | $36$ |
| $1000$ | $1^{\circ}00'55''$ | $113$ |
Wie bereits erwähnt ist Formel (1) nur gültig, wenn die Höhe $e$ des Beobachters klein im Verhältnis zum Erdradius $r$ ist.
- Für $e = 10000\;m = 10\;km$ ergibt die Formel $\theta = 3^{\circ}12'40''$, während der korrekte Wert $\theta = 3^{\circ}12'33''$ ist.
- Für $e = 500\;km$ würde die Formel eine Kimmtiefe von $\theta = 22^{\circ}42'21''$ ergeben, statt des korrekten Wertes $\theta = 21^{\circ}59'58''$.
Offensichtlich kann die Kimmtiefe nie größer als $90^{\circ}$ sein, selbst wenn sich der Beobachter in unendlich großer Entfernung befindet. Natürlich wird im Vorstehenden angenommen, dass sich der Horizont des Beobachters auf Meereshöhe befindet. Es ist klar, dass, wenn sich der Beobachter auf einem ausgedehnten Plateau befindet, selbst in einer Höhe von 2 oder 5 Kilometern, die tatsächliche Kimmtiefe seines Horizonts nur der Höhe seiner Augen über seinen Füßen entspricht.
Einfluss auf die Zeiten von Sonnenaufgang und Sonnenuntergang
Wenn man auf einem Berggipfel steht, muss man „nach unten“ schauen, um den Horizont zu sehen. Die Sonne steht also tatsächlich tiefer als die Augen, wenn sie auf- oder untergeht. Um wie viel wird der Sonnenaufgang dadurch verfrüht bzw. der Sonnenuntergang verzögert, weil sich der Horizont absenkt? Um das herauszufinden, muss man diese Kimmtiefe durch die Rate teilen, mit der die Sonne höher oder tiefer steigt.
Im Folgenden wird angenommen, dass sich der lokale Stundenwinkel der Sonne während 24 Stunden um genau 360° vergrößert. Mit den gegenwärtigen Werten der Orbitalelemente der Erde kann die tägliche Variation im Laufe des Jahres zwischen den Extremwerten $359\overset{\circ}{.}88$ und $360\overset{\circ}{.}09$ pro Tag variieren.
Die Höhe $h$ der Sonne ergibt sich aus
$$\sin(h) = \sin(\delta_{\odot})\cdot\sin(\beta_0) + \cos(\delta_{\odot})\cdot\cos(\beta_0)\cdot\cos (\tau)\tag{2}$$
wobei $\delta_{\odot}$ die Deklination der Sonne, $\beta_0$ die geografische Breite des Beobachters und $\tau$ der Stundenwinkel der Sonne ist. Wenn man die 1. Ableitung beider Elemente dieser Formel nach der Zeit nimmt, erhält man (unter Berücksichtigung der Konstanz von $\beta_0$ und Vernachlässigung der sehr kleinen Variation von $\delta_{\odot}$)
$$\cos(h)\cdot \textrm{d}h = -\cos(\delta_{\odot})\cdot\cos(\beta_0)\cdot\sin(\tau)\cdot\textrm{d}\tau\tag{3}$$
bzw., weil am Horizont $\cos(h) = 1$ gilt,
$$\textrm{d}h = -\cos(\delta_{\odot})\cdot\cos(\beta_0)\cdot\sin(\tau)\cdot\textrm{d}\tau\tag{4}$$
Hier ist $\textrm{d}\tau$ die Variation des Stundenwinkels der Sonne ($360^{\circ}$ pro Tag oder $1^{\circ}$ alle 240 Sekunden) und $\textrm{d}h$ die Variation ihrer Höhe, ausgedrückt in denselben Einheiten wie $\textrm{d}\tau$. Der Wert von $\sin(\tau)$ kann aus der Tatsache abgeleitet werden, dass man am Horizont (unter Vernachlässigung der Lichtbrechung) $\cos(\tau) = -\tan(\delta_{\odot})\cdot \tan(\beta_0)$ gegeben hat.
Man sieht jetzt, dass der Faktor $A = \cos(\delta_{\odot})\cdot\cos(\beta_0)\cdot\sin(\tau)$ nicht vom Vorzeichen von $\delta_{\odot}$ oder $\beta_0$ abhängt, da der Kosinus eine gerade Funktion ist.
Am Äquator ist $\sin(\tau) = 1$ (oder $-1$) für alle Deklinationen, aber $A = 1$ nur bei den Tagundnachtgleichen. Wenn $\delta_{\odot}$ von $0^{\circ}$ abweicht, ist $A \lt 1$, obwohl der Tagesweg der Sonne senkrecht zum Horizont ist. Für eine gegebene geografische Breite ist die Größe $A$ am größten zur Tagundnachtgleiche und am kleinsten zur Sonnenwende. Sie nimmt beispielsweise folgende Werte an:
| Tabelle 2 | ||
|---|---|---|
| $\beta_0$ | Tag-/Nachtgleichen | Sonnwenden |
| $0 ^{\circ}$ | $1 $ | $0.9175$ |
| $30^{\circ}$ | $0.8660$ | $0.7693$ |
| $40^{\circ}$ | $0.7660$ | $0.6547$ |
| $50^{\circ}$ | $0.6428$ | $0.5050$ |
| $55^{\circ}$ | $0.5736$ | $0.4133$ |
| $60^{\circ}$ | $0.5000$ | $0.3031$ |
| $65^{\circ}$ | $0.4226$ | $0.1430$ |
Beispiel
Die Augen eines Beobachters befinden sich in einer Höhe von $50$ Metern über dem Meeresspiegel. Bei dieser Höhe beträgt die Kimmtiefe $0^{\circ}13'37''$ oder $0\overset{\circ}{.}2270$ (siehe Tabelle 1). Weiter nimmt man an, der Beobachter befinde sich auf $\beta_0 = 48^{\circ}$ Breite (Nord oder Süd) und die Deklination der Sonne betrage $\delta_{\odot} = +20^{\circ}$.
Die obige Formel (4) ergibt dann den Vorfaktor
$\textrm{d}h = 0.57512\cdot\textrm{d}\tau$
Da $\textrm{d}h$ hier der Kimmtiefe entspricht, erhält man
$\textrm{d}\tau = \frac{\textrm{d}h}{0.57512} = \frac{0\overset{\circ}{.}2270}{0.57512} = 0\overset{\circ}{.}3947$
was einem Unterschied von $95$ Sekunden gegenüber dem theoretischen (Meeresspiegel-)Sonnenauf- oder untergang entspricht! Eine Person, die sich im obersten Stockwerk eines hohen Gebäudes aufhält, könnte theoretisch den Aufgang des oberen Randes der Sonne beobachten, dann eilig mit dem Aufzug nach unten fahren und den Sonnenaufgang ein zweites Mal sehen!