Inhaltsverzeichnis
Berechnung der Jahreszeiten
Per Definition sind die Zeiten der Tagundnachtgleichen und Sonnenwenden jene Zeitpunkte, an denen die scheinbare geozentrische Länge der Sonne $\lambda_{\odot}$ (d.h. berechnet unter Einbeziehung der Effekte von Aberration und Nutation) ein ganzzahliges Vielfaches von $90^{\circ}$ Grad ist. Weil die ekliptikale Breite der Sonne nicht genau Null ist, ist die Deklination $\delta_{\odot}$ der Sonne zum Zeitpunkt der Tagundnachtgleichen nicht genau Null.
| Tabelle 1 | |
|---|---|
| Event | Länge der Sonne |
| Frühlingsäquinoktium | $\lambda_{\odot} = 0^{\circ}$ |
| Sommersolstitium | $\lambda_{\odot} = 90^{\circ}$ |
| Herbstäquinoktium | $\lambda_{\odot} = 180^{\circ}$ |
| Wintersolstitium | $\lambda_{\odot} = 270^{\circ}$ |
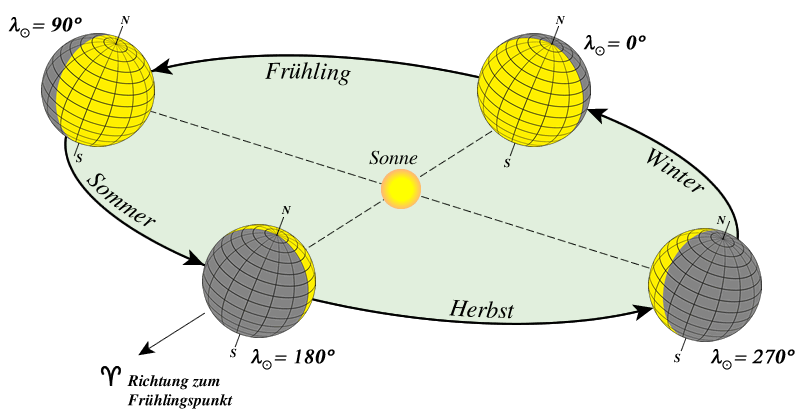
Abb.1 zeigt in übertriebener Darstellung den Lauf der Jahreszeiten. Man beachte die Neigung der Erdachse von ca. $23\overset{\circ}{.}5$ gegen die Ekliptik. Im Sommer ist die Nordhalbkugel der Erde zur Sonne geneigt, die Erde befindet sich jedoch in größerer Entfernung von der Sonne als im Winter.
Hohe Genauigkeit lässt sich erzielen, indem man tatsächlich den Wert der scheinbaren geozentrischen Länge der Sonne $\lambda_{\odot}$ für einige Zeitpunkte nahe des gewüschten Ereignisses berechnet und dann durch Interpolation den Zeitpunkt ermittelt, zu dem die Länge genau $0^{\circ}$, $90^{\circ}$, $180^{\circ}$ bzw. $270^{\circ}$ beträgt. Die Bewegung der Sonne entlang der Ekliptik beträgt pro Tag etwa $3548''$, daher führt ein Fehler von $1''$ in berechneter Länge zu einem Fehler von etwa 24 Sekunden in den Zeiten der Tagundnachtgleiche oder Sonnenwende.
Näherungsverfahren von Meeus
J. Meeus gibt in den Astronomical Algorithms ein Näherungsverfahren zur Berechnung dieser Zeitpunkte an. Man ermittelt zunächst den Zeitpunkt der „mittleren“ Tagundnachtgleiche oder Sonnenwende, indem man den entsprechenden Ausdruck in Tabelle 2 bzw. Tabelle 3 verwendet, mit dem Hilfswert
$$J = \frac{Jahr - 2000}{1000}\tag{1}$$
Wichtig ist hier, dass die Jahreszahl $Jahr$ eine Ganzzahl (Integer) sein muss! Die mittleren Zeitpunkte $JDE_{0}$ sind nun Polynome in der Hilfsvariablen $J$. Es ist auf den Zeitraum zu achten, für die diese Beziehungen gültig sind!
| Tabelle 2: Mittlere Zeitpunkte der Äquinoktien/Solstitien für den Zeitraum $-1000$ bis $+1000$ | |
|---|---|
Frühlingsäquinoktium  | \(\begin{align} JDE_{0} &= 1721139.29189\\ &+ 365242.13740\cdot J\\ &+ 0.06134\cdot J^2\\ &+ 0.00111\cdot J^3\\ &- 0.00071\cdot J^4 \end{align}\) |
Sommersolstitium  | \(\begin{align} JDE_{0} &= 1721233.25401\\ &+ 365241.72562\cdot J\\ &- 0.05323\cdot J^2\\ &+ 0.00907\cdot J^3\\ &+ 0.00025\cdot J^4 \end{align}\) |
Herbstäquinoktium  | \(\begin{align} JDE_{0} &= 1721325.70455\\ &+ 365242.49558\cdot J\\ &- 0.11677\cdot J^2\\ &- 0.00297\cdot J^3\\ &+ 0.00074\cdot J^4 \end{align}\) |
Wintersolstitium  | \(\begin{align} JDE_{0} &= 1721414.39987\\ &+ 365242.88257\cdot J\\ &- 0.00769\cdot J^2\\ &- 0.00933\cdot J^3\\ &- 0.00006\cdot J^4 \end{align}\) |
| Tabelle 3: Mittlere Zeitpunkte der Äquinoktien/Solstitien für den Zeitraum $+1000$ bis $+3000$ | |
|---|---|
Frühlingsäquinoktium  | \(\begin{align} JDE_{0} &= 2451623.80984\\ &+ 365242.37404\cdot J\\ &+ 0.05169\cdot J^2\\ &- 0.00411\cdot J^3\\ &- 0.00057\cdot J^4 \end{align}\) |
Sommersolstitium  | \(\begin{align} JDE_{0} &= 2451716.56767\\ &+ 365241.62603\cdot J\\ &+ 0.00325\cdot J^2\\ &+ 0.00888\cdot J^3\\ &- 0.0003\cdot J^4 \end{align}\) |
Herbstäquinoktium  | \(\begin{align} JDE_{0} &= 2451810.21715\\ & + 365242.01767\cdot J\\ &- 0.11575\cdot J^2\\ &+ 0.00337\cdot J^3\\ &+ 0.00078\cdot J^4 \end{align}\) |
Wintersolstitium  | \(\begin{align} JDE_{0} &= 2451900.05952\\ &+ 365242.74049\cdot J\\ &- 0.06223\cdot J^2\\ &- 0.00823\cdot J^3\\ &+ 0.00032\cdot J^4 \end{align}\) |
Die Zeitpunkte sind hier als julianischer Ephemeridentag $JDE_{0}$ in der Zeitskala der dynamischen Zeit $TD$ angegeben.
Dann berechnet man die Werte $T, W$ und $\Delta\lambda$ wie folgt:
\[\begin{align} T &= \frac{(JDE_{0} - 2451545.0)}{36525}\\\\ W &= 35999\overset{\circ}{.}373\cdot T - 2\overset{\circ}{.}47\\\\ \Delta\lambda &= 1 + 0.0334\cdot \cos (W)\\ &+ 0.0007\cdot \cos (2\cdot W) \end{align}\tag{2}\]
Nun benötigt man die Summe $S$ der Korrekturterme, die in Tabelle 4 gelistet sind. Die erste Spalte ist nur die Nummerierung der Terme und dient zur Referenzierung, es sind keine Rechenwerte.
| Tabelle 4: Korrekturterme in $''$ | |||
|---|---|---|---|
| n | A$['']$ | B$[^{\circ}]$ | C$\big[\frac{\circ}{Jht.}\big]$ |
| $01$ | $485$ | $324.96$ | $1934.136 $ |
| $02$ | $203$ | $337.23$ | $32964.467 $ |
| $03$ | $199$ | $342.08$ | $20.186 $ |
| $04$ | $182$ | $27.85 $ | $445267.112$ |
| $05$ | $156$ | $73.14 $ | $45036.886 $ |
| $06$ | $136$ | $171.52$ | $22518.443 $ |
| $07$ | $77 $ | $222.54$ | $65928.934 $ |
| $08$ | $74 $ | $296.72$ | $3034.906 $ |
| $09$ | $70 $ | $243.58$ | $9037.513 $ |
| $10$ | $58 $ | $119.81$ | $33718.147 $ |
| $11$ | $52 $ | $297.17$ | $150.678 $ |
| $12$ | $50 $ | $21.02 $ | $2281.226 $ |
| $13$ | $45 $ | $247.54$ | $29929.562 $ |
| $14$ | $44 $ | $325.15$ | $31555.956 $ |
| $15$ | $29 $ | $60.93 $ | $4443.417 $ |
| $16$ | $18 $ | $155.12$ | $67555.328 $ |
| $17$ | $17 $ | $288.79$ | $4562.452 $ |
| $18$ | $16 $ | $198.04$ | $62894.029 $ |
| $19$ | $14 $ | $199.76$ | $31436.921 $ |
| $20$ | $12 $ | $95.39 $ | $14577.848 $ |
| $21$ | $12 $ | $287.11$ | $31931.756 $ |
| $22$ | $12 $ | $320.81$ | $34777.259 $ |
| $23$ | $9 $ | $227.73$ | $1222.114 $ |
| $24$ | $8 $ | $15.45 $ | $16859.074 $ |
Jeder Korrekturterm hat die Form
$$ A\cdot \cos\big(B + C\cdot T\Big)\tag{3}$$
also ist $S$
\[\begin{align} S =&\; 485\cdot \cos(324\overset{\circ}{.}96 + 1934\overset{\circ}{.}136\cdot T)\\ &+ 203\cdot \cos(337\overset{\circ}{.}23 + 32964\overset{\circ}{.}467\cdot T)\\ &+ 199\cdot \cos(342\overset{\circ}{.}08 + 20\overset{\circ}{.}186\cdot T)\\ &+\dots\\ & \textsf{usw.} \end{align}\tag{4}\]
Die Argumente des Cosinus sind dabei im Gradmaß gegeben, eine eventuelle Umrechnung auf Radiant könnte erforderlich sein.
Die Zeitpunkte der korrigierten Werte in julianischen Tagen erhält man nun über
$$ JDE = JDE_{0} +\frac{S\cdot 10^{-5}}{\Delta\lambda}\tag{5}$$
Die Umrechnung des julianischen Tages in ein Kalenderdatum ergibt dann den Zeitpunkt in dynamischer Zeit $TD$. Mit Hilfe von $\Delta T$ kann der Zeitpunkt dann in Weltzeit $UT$ zurückgerechnet werden.
Beispiel 1
 Man berechne den Zeitpunkt des Sommersolstitiums für das Jahr 2024!
Man berechne den Zeitpunkt des Sommersolstitiums für das Jahr 2024!
Das Jahr ist $2024$, also erhält man
$J = \frac{2024 - 2000}{1000} = 0.024$
Für die Sommersonnenwende im Zeitraum $+1000$ bis $+3000$ nimmt man die 2. Gleichung aus Tabelle 3 und erhält für den mittleren Zeitpunkt
\(\begin{align} JDE_{0} &= 2451716.56767\\ &+ 365241.62603\cdot 0.024\\ &+ 0.00325\cdot 0.024^2\\ &+ 0.00888\cdot 0.024^3\\ &- 0.0003\cdot 0.024^4\\ &= 2460482.366696715 \end{align}\)
Nun berechnet man sukzessive $T, W$ und $\Delta\lambda$, nämlich
\(\begin{align} T &= \frac{(2460482.366696715 - 2451545.0)}{36525}\\ &= 0.244691764454891\\\\ W &= 35999\overset{\circ}{.}373\cdot 0.244691764454891\\ &- 2\overset{\circ}{.}47\\ &= 8808\overset{\circ}{.}75009864 \\ &= 166\overset{\circ}{.}28009864 \\\\ \Delta\lambda &= 1 + 0.0334\cdot \cos (166.28009864)\\ &+ 0.0007\cdot \cos (2\cdot 166.28009864)\\ &= 0.96817426 \end{align}\)
Für große Winkel (hier $W$) kann die Reduktions-Funktion verwendet werden, um den Winkel in das Intervall [0°-360°] zu bringen.
Die Summe der Korrekturterme aus Tabelle 4 ergibt
\(\begin{align} S =&+485\cdot \cos(324\overset{\circ}{.}96 + 1934\overset{\circ}{.}136\cdot T)\\ &+ 203\cdot \cos(337\overset{\circ}{.}23 + 32964\overset{\circ}{.}467\cdot T)\\ &+ 199\cdot \cos(342\overset{\circ}{.}08 + 20\overset{\circ}{.}186\cdot T)\\ &\quad\quad\vdots\quad\quad\vdots\\ &+ 8\cdot \cos(15\overset{\circ}{.}45 + 16859\overset{\circ}{.}074\cdot T)\\ &= 270\overset{''}{.}33103 \end{align}\)
und damit folgt der korrigierte julianische Tag
\(\begin{align} JDE &= JDE_{0} +\frac{S\cdot 10^{-5}}{\Delta\lambda}\\ &= 2460482.366696715 +\frac{270\overset{''}{.}33103\cdot 10^{-5}}{0.96817426\frac{''}{d}}\\ &= 2460482.36949 \end{align}\)
Eine Rückrechnung auf das Kalenderdatum liefert dann den 20. Juni 2024, 20:52:03 $TD$. Von dieser dynamischen Zeit wird nun der Wert von $\Delta T$ abgezogen, denn es gilt ja
$ UT = TD - \Delta T $
Im Jahr 2024 beträgt $\Delta T = 69^{s} = 1^{m}09^{s}$, also erhält man die Uhrzeit
$\textrm{20:52:03} - 1^{m}09^{s} = \textrm{20:50:54}$
also den 20. Juni 2024, 20:50:54 $UT$.
Eine exakte Berechnung gemäß der Planetentheorien liefert den 20. Juni 2024, 20:51:57 $TD$ = 20:50:48 $UT$. Für die meisten Zwecke ist es ausreichend, die Zeitpunkte auf ganze Minuten zu runden.
Für die mitteleuropäische Sommerzeit, also $UT + 2^{h}$, erhält man daher den 20. Juni 2024, 22:51 MESZ.
Eine Berechnung für die Jahre 2000-2100 zeigt, dass im Jahre 2007 das Frühlingsäquinoktium das letzte Mal auf den 21.3. fiel (dynamische Zeit!). Seither fielen alle Frühlingsanfänge auf den 20.3. des Jahres. Im Jahre 2044 wird der Frühlingsbeginn dann auf den 19.3. 2044, 23:21 $UT$ fallen.
Genauigkeit
Die Genauigkeit des oben angeführten Näherungsalgorithmus von J. Meeus wurde für den Zeitraum $1800 - 2200$ getestet und mit den Daten der Software Alcyone verglichen. Nachstehend wiedergegeben sind die Abweichungen in Sekunden vom jeweiligen exakten Wert.
Äquinoktien und Solstitien 1900-2100
Für den Jahreszeitraum 1900 bis 2100 wurden die Äquinoktien (Tag-Nacht-Gleichen) und Solstitien (Sonnwenden) mit den auf diesen Seiten vorgestellten Algorithmen berechnet. Die Ergebnisse sind jeweils auf die nächste ganze Minute gerundet und werden in Weltzeit $UT$ angegeben. Für Mitteleuropa (Zeitzone MEZ bzw. MESZ) ist gegebenenfalls 1 Stunde (MEZ) oder 2 Stunden (MESZ) zu addieren.
Man beachte eventuelle Tagesüberläufe beim Umrechnen in MEZ bzw. MESZ!
Es ist z.B. der Herbstbeginn 2030 am $22.09.2030, \;\textrm{23:27}\;UT$. Die Umrechnung in mitteleuropäische Sommerzeit ergibt dann den Zeitpunkt $22.09.2030, \;\textrm{23:27}\;UT + 2^{h} = 2\color{#ff0000}{3}.09.2030, \;\textrm{01:27}\;MESZ$