Inhaltsverzeichnis
Auf- und Untergangszeiten
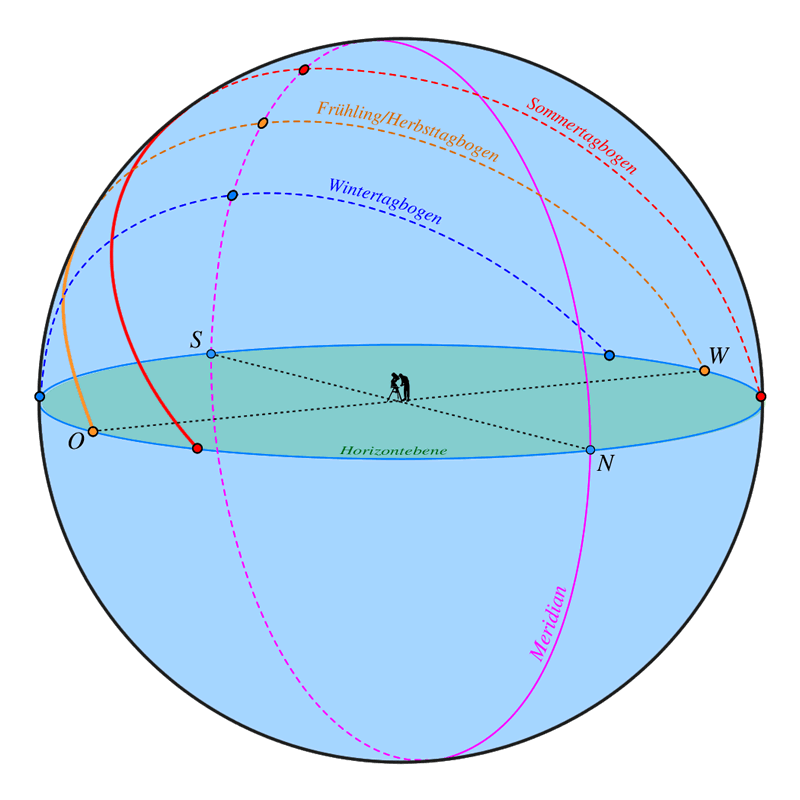
Die Auf-, Kulminations- und Untergangszeiten lassen sich für die Sonne und die Planeten rasch berechnen. Für den Mond wird aufgrund seiner hohen Eigenbewegung das iterative Verfahren vorgestellt. Als erstes wird die Höhe am Horizont benötigt. Diese ist aufgrund der Refraktion und der Parallaxe nicht $0$.
Sonne, Sterne und Planeten
| Tabelle 1 | |||
|---|---|---|---|
| Himmelsobjekt | Höhe $h$ | Dämmerungen | Höhe $h$ |
| Sonne: | $h$ = $-0^{\circ} 50'$ | bürgerlich: | $h$ = $-6^{\circ}$ |
| Mond: | $h$ = $+0^{\circ} 08'$ | nautisch: | $h$ = $-12^{\circ}$ |
| Sonstige: | $h$ = $-0^{\circ} 34'$ | astronomisch: | $h$ = $-18^{\circ}$ |
Hat man die Höhen gefunden, so berechnet man als nächstes den halben Tagbogen, der zwischen $0^h$ und $12^h$ liegen muß:
$$\cos(15^h\cdot t) = \frac{\sin(h) - \sin(\beta_0) \cdot \sin(\delta)}{\cos(\beta_0) \cdot \cos(\delta)}\tag{1}$$
Hinzugezogen werden noch die mittleren Änderungen des Stundenwinkels $\mu$:
| Tabelle 2 | |
|---|---|
| Himmelsobjekt | $\mu$ - Wert |
 Sterne: | $\mu_s$ = 1.00273790931 |
 Sonne: | $\mu_S$ = 1.0 |
 Merkur: | $\mu_1$ = 0.99137019529 |
 Venus: | $\mu_2$ = 0.99828744065 |
 Erde: | $\mu_3$ = $\mu_S$ |
 Mars: | $\mu_4$ = 1.00128215634 |
 Jupiter: | $\mu_5$ = 1.00250699424 |
 Saturn: | $\mu_6$ = 1.00264485961 |
 Uranus: | $\mu_7$ = 1.00270521758 |
 Neptun: | $\mu_8$ = 1.00272118691 |
 Pluto: | $\mu_9 \approx \mu_s$ |
Die Kulminationszeit lautet:
$$K = \dfrac{\alpha + \tfrac{\lambda_0}{15^h} - GMST}{\mu_p}\tag{2}$$
und die entsprechende Kulminationshöhe ist:
$$h = 90^{\circ} - \beta_0 + \delta\tag{3}$$
Die Aufgangszeit $A$ und die Untergangszeit $U$ sind dann einfach zu ermitteln: $$A = K - \dfrac{t}{\mu_p}\tag{4}$$ $$U = K + \dfrac{t}{\mu_p}\tag{5}$$
$t$ = halber Tagbogen
$\lambda_0$, $\beta_0$ = geographische Koordinaten des Beobachters
$\alpha$, $\delta$ = äquatoriale Koordinaten des Himmelsobjekts
$GMST$ = mittlere Greenwich Sternzeit (Greenwich mean siderial time) um 00:00 Uhr $UT$
Beispiel 1
Man berechne die Aufgangs-, Kulminations- und Untergangszeit der Sonne für den 21.5.2023 für die Position $\lambda_0 = 10^{\circ}$ Ost und $\beta_0 = 50^{\circ}$ Nord mit dem schnellen Algorithmus.
Für die Sonne gilt als Auf/Untergangshöhe $h = -50' = -0\overset{\circ}{.}833333$. Man benötigt weiters die geozentrischen äquatorialen Koordinaten $\alpha_{\odot}, \delta_{\odot}$ für die Sonne um $\textrm{00:00}\;UT$ des gegebenen Tages und die mittlere Sternzeit $GMST$ in Greenwich für denselben Zeitpunkt, sowie die mittlere Schiefe der Ekliptik $\varepsilon_0$.
Man kann die topozentrischen Koordinaten der Sonne verwenden. Die Sonnenparallaxe ist aber relativ klein mit etwa $8\overset{''}{.}749$ und liegt weit unterhalb der Genauigkeit dieses Algorithmus. Topozentrische Koordinaten lohnen sich nur beim Erdmond.
Für den gegebenen Zeitpunkt wurde der julianische Tag für $\textrm{08:15}\;UT$ in diesem Beispiel bereits ermittelt zu $JD = 2460085.84375$. Man benötigt hier jedoch den Zeitpunkt um Mitternacht, und der julianische Tag (mit Endung auf $.5$) lautet daher $JD = 2460085.5$. Weiters addiert man für die Sonnenkoordinaten noch den Wert von $\Delta T = 69^{s}$ für das Jahr 2023, daher ist der julianische Ephemeridentag
\(\begin{align} JDE &= JD + \frac{69^{s}}{86400\tfrac{s}{d}}\\ &= 2460085.500798611 \end{align}\)
Die Korrektur von $\Delta T$ kann im Rahmen der hier erwarteten Genauigkeit auch weggelassen werden.
Daraus folgen die julianischen Jahrhunderte bezüglich der Epoche $J2000$ mit
\(\begin{align} T &= \frac{JDE - 2451545.0}{36525}\\ &= \frac{2460085.500798611 - 2451545.0}{36525}\\ &= 0.23382616833979386 \end{align}\)
Die Sonnenkoordinaten können nun mit dem schnellen Algorithmus laut J. Meeus analog zu diesem Beispiel ermittelt werden, man erhält die ekliptikale geozentrische Länge der Sonne mit
\(\begin{align} \lambda &= 8699\overset{\circ}{.}712371322292\\ &= 59\overset{\circ}{.}712371\\ \end{align}\)
Die Breite $\beta$ der Sonne wird hier $0$ gesetzt.
Zur Umrechnung in äquatoriale geozentrische Koordinaten benötigt man die mittlere Schiefe der Ekliptik mit dieser Gleichung zu
\(\begin{align} \varepsilon_0 &= \big(84381\overset{''}{.}448\\ &- 46\overset{''}{.}8150\cdot T\\ &- 0\overset{''}{.}00059\cdot T^2\\ &+ 0\overset{''}{.}001813\cdot T^3\big)/3600\tfrac{''}{\circ}\\ &= 84370\overset{''}{.}50141884918/3600\tfrac{''}{\circ}\\ &= 23\overset{\circ}{.}436250 \end{align}\)
Da man sich nicht allzu weit von der Epoche $J2000$ entfernt befindet kann man die Terme für $T^2$ und $T^3$ hier auch vernachlässigen.
Auf die Korrektur der Ekliptikschiefe mit dem Faktor $+0.00256\cdot \cos \Omega$ wird im Rahmen der Genauigkeit hier verzichtet. Die geozentrische Rektaszension der Sonne ist gegeben durch die Beziehung
\(\begin{align} \alpha_{\odot} &= \textrm{arctan2}\left(\frac{\cos (\varepsilon_0)\cdot\sin (\lambda)}{\cos (\lambda)} \right)\\ &= 57\overset{\circ}{.}520028 \end{align}\)
Es ist auf die Darstellung von $\alpha_{\odot}$ im korrekten Quadranten zu achten.
Die Deklination der Sonne erhält man über
\(\begin{align} \delta_{\odot} &= \arcsin\left(\sin (\varepsilon_0)\cdot\sin (\lambda) \right)\\ &= 20\overset{\circ}{.}086615 \end{align}\)
Die mittlere Sternzeit in Greenwich berechnet man mit dem nicht um $\Delta T$ korrigierten Wert des julianischen Tages $JD = 2460085.5$ mithilfe dieser Beziehung (für $\textrm{00:00}$ Uhr) mit
| \( \begin{align} GMST &= +6\overset{h}{.}6563064033\\ &+ 0\overset{h}{.}06570982442\cdot (JD(0^h\,UT) - 2445700.5)\\ &= 951\overset{h}{.}892130685 \end{align} \) |
Mithilfe der $\textrm{trunc}$-Funktion erhält man die Eingrenzung auf das Intervall [$0^{h}-24^{h}$] mit
| \(\begin{align} &\textrm{trunc} \left(\frac{951\overset{h}{.}892130685}{24^{h}} \right) = 39\\ &951\overset{h}{.}892130685 - 39\cdot 24^{h} = 15\overset{h}{.}892130685 \end{align}\) |
Dies ist ein Stundenwert und wird durch Mulitplikation mit $15$ in Grad umgewandelt.
\(\begin{align} GMST &= 15\overset{h}{.}892130685\cdot 15\frac{\circ}{h}\\ &= 238\overset{\circ}{.}381960 \end{align}\)
Nun hat man sämliche Werte für $\alpha_{\odot}, \delta_{\odot}, GMST$ sowie die geografische Länge $\lambda_0 = -10^{\circ}$ (Ost negativ!) in Grad gegeben. Die Kulminationszeit $K$ ist dann
\(\begin{align} K &= \frac{\alpha + \lambda_0 - GMST}{(\mu_{S}\cdot 15)}\\ &= \frac{57\overset{\circ}{.}520028 - 10^{\circ} - 238\overset{\circ}{.}381960}{(1\cdot 15\frac{\circ}{h})}\\ &= -12\overset{h}{.}72412957 \end{align}\)
wobei der Faktor $\mu_{S}$ für die Sonne laut oben stehender Tabelle $\mu_{S} = 1$ ist. Um die Kulminationszeit in das Intervall [$0^{h}-24^{h}$] zu bringen, wird $24^{h}$ addiert und man erhält
$K = 11\overset{h}{.}27587043$
Die Umrechnung in Stunden/Minuten/Sekunden ergibt
\(\begin{align} &\textrm{trunc}(11\overset{h}{.}27587043) = 11^{h}\\ &\textrm{frac}(11\overset{h}{.}27587043)\cdot 60\tfrac{m}{h}\\ & = 0\overset{h}{.}27587043\cdot 60\tfrac{m}{h} = 16\overset{m}{.}5522258\\ &\textrm{frac}(16\overset{m}{.}5522258)\cdot 60\tfrac{s}{m}\\ & = 0\overset{m}{.}5522258\cdot 60\tfrac{s}{m} = 33\overset{s}{.}1 \end{align}\)
Die Formel für den halben Tagbogen (in Grad) mit der Refraktionshöhe der Sonne von $-50' = -0\overset{\circ}{.}833333$ und der geografischen Breite $\beta_0 = 50^{\circ}$ lautet
| \(\begin{align} \cos(15^h\cdot t) &= \frac{\sin(h) - \sin(\beta_0) \cdot \sin(\delta)}{\cos(\beta_0) \cdot \cos(\delta)}\\ &=\frac{\sin (-0\overset{\circ}{.}083333) - \sin (50\overset{\circ}{.}0) \cdot\sin (20\overset{\circ}{.}086615))}{\cos (50\overset{\circ}{.}0)\cdot \cos (20\overset{\circ}{.}086615)}\\ &= -0.45989590 \end{align}\) |
Damit folgt
\(\begin{align} 15\cdot t &= \arccos (-0.45989590) = 117\overset{\circ}{.}38039039\\ t &= \frac{117\overset{\circ}{.}38039039}{15\frac{\circ}{h}}\\ t &= 7\overset{h}{.}82535936 \end{align}\)
Aufgangszeit:
\(\begin{align} A &= K - \frac{t}{\mu_{S}}\\ &= 11\overset{h}{.}27587043 - \frac{7\overset{h}{.}82535936}{1}\\ &= 3\overset{h}{.}45051107 \end{align}\)
Untergangszeit:
\(\begin{align} U &= K + \frac{t}{\mu_{S}}\\ &= 11\overset{h}{.}27587043 + \frac{7\overset{h}{.}82535936}{1}\\ &= 19\overset{h}{.}10122979 \end{align}\)
Die Umwandlung in Stunden/Minuten/Sekunden erfolgt analog wie oben zu $K$ und ergibt gerundet
\(\begin{align} &A = 3^h 27^m 2^s = 3^h 27^m\\ &U = 19^h 6^m 4^s = 19^h 6^m \end{align}\)
Diese Zeitpunkte gelten natürlich für die lokale Zeit (hier: MOZ). Die Umrechnung in die Sommerzeit kann noch angebracht werden. Sie gilt dann allerdings für den lokalen Meridian.
Die Astronomiesoftware GUIDE gibt für den gegebenen Tag die folgenden Daten an:
| Event | hier | GUIDE |
|---|---|---|
| Aufgang | $3^h 27^m \;UT$ | $3^h 27^m \;UT$ |
| Kulmination | $11^h 17^m \;UT$ | $11^h 17^m \;UT$ |
| Untergang | $19^h 6^m \;UT$ | $19^h 7^m \;UT$ |
Bei Höhen von wenigen Grad bzw. wenn sich Objekte an ihrem Auf-/Untergangspunkt befinden, sind die Ergebnisse der Formeln für die Refraktion mit Vorsicht zu beurteilen. In der Nähe des Horizonts spielen unvorhersehbare Störungen der Atmosphäre eine große Rolle. Nach Untersuchungen von B. Schaefer und W. Liller (1990) schwankt die Refraktion am Horizont normalerweise um $0\overset{\circ}{.}3 = 18'$ um den Mittelwert, teilweise auch deutlich mehr. Es macht daher keinen Sinn, die Auf- oder Untergangszeiten eines Himmelskörpers genauer als auf ganze Minuten anzugeben.
Erdmond
Iterationsverfahren
Hier wird das iterative Verfahren aus O. Montenbruck (Grundlagen der Ephemeridenrechnung) vorgestellt, dass rechentechnisch einen höheren Aufwand hat. Man startet mit dem Zeitpunkt
$$T_0 = 12^h\tag{6}$$
der mittleren Orts-Sternzeit
$$\Theta_0 = LMST\tag{7}$$
aus dem Abschnitt über die Sternzeit im ersten Durchgang und
$$\Theta_{i+1} = \Theta_i + 1.00273790931\cdot (T_{i+1} − T_i)\tag{8}$$
im nachfolgenden Durchgang. Es wird die „geozentrische“ Höhe verwendet, sie lautet für den Mond:
$$h_0 = + 0^{\circ} 08' = 0\overset{\circ}{.}1333\dots\tag{9}$$
Jetzt müssen die äquatorialen Koordinaten $\alpha_i$, $\delta_i$ des Mondes zum Zeitpunkt $T_i$ berechnet werden. Dann benötigt man den Stundenwinkel
$$\tau_i = \Theta_i - \alpha_i\tag{10}$$
und den halben Tagbogen
$$\cos(15^h\cdot t_i) = \frac{\sin(h_0) - \sin(\beta_0) \cdot \sin(\delta_i)}{\cos(\beta_0) \cdot \cos(\delta_i)}\tag{11}$$
der negativ in der östlichen Hemisphäre, positiv in der westlichen Hemisphäre und $t_i = 0$ in der Kulmination ist. Nun wird die zeitliche Änderung des Stundenwinkels $\mu_i$ speziell für den Mond berechnet:
$$\mu_i = 1.0027 - \frac{\alpha_{i} − \alpha_{i-1}}{T_{i} - T_{i-1}}\tag{12}$$
mit
$$\frac{\alpha_1 − \alpha_0}{T_1 - T_0} = 0.0366\tag{13}$$
im ersten Iterationschritt $i=0$. Die gesuchte Zeit ist dann
$$T_{i+1} = T_i + \frac{t_i - \tau_i}{\mu_i}\tag{14}$$
Hat man den neuen Wert $T_i$ berechnet, so muss man nun die geozentrisch äquatorialen Koordianten des Mondes $\alpha_i$ und $\delta_i$ erneut berechnen und dann mit den neuen Werten zur Sternzeit $\Theta_i$ springen. Der Durchlauf startet solange erneut, bis ein genügend geringer Differenzwert zwischen $T_{i+1}$ und $T_i$ gefunden wird.
Das iterative Verfahren wird in Stunden berechnet, nicht in Grad. Man sollte während der Iteration eine Reduktion auf ein Intervall zwischen $0^h$ und $24^h$ vermeiden, denn das stört die Iteration erheblich.
Da der Mond bei seinem Umlauf um die Erde von West nach Ost weiterwandert, steht er länger als alle anderen Himmelskörper mit fast derselben Deklination am Himmel. Dadurch verspäten sich die Mondauf- und -untergänge im Durchschnitt um etwa $50^{m}$ pro Tag. Das hat zur Folge, dass es in jedem Monat einen Tag gibt, an dem kein Mondaufgang stattfindet und einen weiteren Tag, an dem der Mond nicht untergeht. Dann ist $T_i$ im Laufe der Iteration negativ oder größer als 24$^h$. Es findet dann das Ereignis am Vortag oder am nächsten Tag statt. Gegebenenfalls kann man einen um $\frac{24^h}{μ}$ vergrößerten oder verkleinerten Wert von $T_i$ benutzen.
Beispiel 2
Man berechne den Zeitpunkt (in $MEZ$) des Mondaufgangs am 16.1.2001 für den Ort $\lambda_0 = 15^{\circ}\;$Ost und $\beta_0 = 50^{\circ}\;$Nord.
Beim Mond kann es vorkommen, dass er an einem bestimmten Datum nicht aufgeht oder auch nicht untergeht. Das entsprechende Event findet dann jeweils einen Tag davor oder einen Tag danach statt. Im nachfolgenden Beispiel ist dies der Fall. Natürlich führt man die praktische Berechnung mit Hilfe einer Schleife durch, hier werden die einzelnen Schritte explizit angeführt.
Schritt 0
Als Startwert nimmt man z.B.
$16.1.2001,\;\textrm{12:00 MEZ}\; \hat{=}\; 16.1.2001,\;\textrm{11:00 UT}$
Man berechnet zunächst den julianischen Tag für $\textrm{00:00}$ Uhr (zur Berechnung der Sternzeit benötigt) und erhält
$JD_{00^h} = 2451925.50000$
Die mittlere Sternzeit in Greenwich um $\textrm{11:00 UT}$ ist dann
\(\begin{align} \Theta_{GW} =& +6\overset{h}{.}664520\\ &+ 0\overset{h}{.}0657098244\cdot (JD_{00^h}- 2451544.5)\\ &+ 1.0027379093\cdot (11^h)\\ &= 42\overset{h}{.}730080 \end{align}\)
Die Ortssternzeit $\Theta_0$ auf der Länge $-15^{\circ}$ (Ost = negativ!) ergibt sich durch Addition von
\(\begin{align} \Theta_0 &= \Theta_{GW} - \frac{-15^{\circ}}{15\frac{\circ}{h}}\\ &= 43\overset{h}{.}730080 \end{align}\)
Die Eingrenzung auf das Intervall [$0^h - 24^h$] liefert ($1\cdot 24^h$ abziehen)
$\Theta_0 = 19\overset{h}{.}730080$
Der Julianische Tag zur Berechnung der schnellen Mondkoordinaten, für $\textrm{11:00 UT}$, ist
\(\begin{align} JD_{11^h} &= JD_{00^h} + \tfrac{11^h}{24\frac{h}{d}}\\ &= 2451925.5 + 0.45833\\ &= 2451925.95833\\ &= JD_0 \end{align}\)
Der Index $0$ steht hier für den „0“-ten Schritt. Die geozentrische Rektaszension bzw. Deklination des Mondes ergeben damit
$\alpha_0 = 13\overset{h}{.}708275$
$\delta_0 = -5\overset{\circ}{.}039420$
Für die Auf- und Untergangsrechnung werden die geozentrischen Koordinaten verwendet. Beim Mond wird die mittlere Refraktionshöhe mit $h_0 = +8' = +0\overset{\circ}{.}133333$ angenommen.
Den Stundenwinkel $\tau_0$ erhält man nun über
\(\begin{align} \tau_0 &= \Theta_0 - \alpha_0\\ &= 19\overset{h}{.}730080 - 13\overset{h}{.}708275\\ & = 6\overset{h}{.}021805 \end{align}\)
Der halbe Tagbogen $t_0$ ist für einen Aufgang negativ zu nehmen und ergibt sich aus dem Cosinus von
| \(\begin{align} \cos(15^h\cdot t_0) &= \frac{\sin(h_0) - \sin(\beta_0) \cdot \sin(\delta_0)}{\cos(\beta_0) \cdot \cos(\delta_0)}\\ &= \frac{\sin(0\overset{\circ}{.}133333) - \sin(50^{\circ}) \cdot \sin(-5\overset{\circ}{.}039420)}{\cos(50^{\circ}) \cdot \cos(-5\overset{\circ}{.}039420)}\\ &= 0.1087255665\dots \end{align}\) |
und damit
\(\begin{align} t_0 &= -\frac{\textrm{arccos}(0.1087255665)}{15\tfrac{\circ}{h}}\\ &= -5\overset{h}{.}583876 \end{align}\)
Nun kann man die nächste genäherte Aufgangszeit ermitteln mittels
\(\begin{align} T_{1} &= T_{0} + \frac{t_0 - \tau_0}{\mu_0}\\ &= 12^h + \frac{-5\overset{h}{.}583876 - 6\overset{h}{.}021805}{0.9661}\\ &= -0\overset{h}{.}01291975\dots \end{align}\)
wobei $\mu_0$ in diesem „0“-ten Schritt $\mu_0 = 1.0027 - \underbrace {0.0366}_{\textsf{konst.}} = 0.9661$ ist.
Nun sieht man, dass die erhaltene Zeit in $MEZ$ negativ ist, das bedeutet, dass das Ereignis am Vortag stattfindet!
Schritt 1
Man belässt nun die neu erhaltene Zeit $T_1$ negativ, muss aber im nächsten Schritt darauf achtgeben, den julianischen Tag zur Berechnung der Mondkoordinaten entsprechend zu korrigieren! Die Sternzeit für diesen (und jeden weiteren) Schritt erhält man über die Beziehnung
| \(\begin{align} \Theta_1 &= \Theta_0 + 1.00273790931\cdot (T_{1} - T_0)\\ &= 19\overset{h}{.}730080 + 1.00273790931 (-0\overset{h}{.}01291975 - 12.0^h)\\ &= 7\overset{h}{.}684270 \end{align}\) |
Der neue julianische Tag ist gegeben über den alten julianischen Tag für $\textrm{00:00}\;UT$, minus $\color{#cc0000}{1}$ Tag plus die neue Zeit $T_1$ (umgerechnet in Tage, wobei für $MEZ - 1 = UT$ wieder eine Stunde abzuziehen ist!)
\(\begin{align} JD_1 &= JD_{00^h} - \color{#cc0000}{1} + \tfrac{(T_1 + 24^h - 1^h)}{24\tfrac{h}{d}}\\ &= 2451925.50000 - 1 + \tfrac{(−0\overset{h}{.}01291975 + 23^h)}{{24\tfrac{h}{d}}}\\ &= 2451925.45780 \end{align}\)
Damit berechnet man nun sukzessive die neuen Mondkoordinaten sowie den neuen Stundenwinkel analog zu Schritt „0“ und erhält
\(\begin{align} \alpha_1 &= 13\overset{h}{.}296006\\ \delta_1 &= -2\overset{\circ}{.}513537\\ \tau_1 &= -5\overset{h}{.}611736 \end{align}\)
Beim halben Tagbogen nimmt man ab jetzt für $\mu_1$ die Beziehung
\(\begin{align} \mu_1 &= 1.0027 - \frac{\alpha_{1} − \alpha_{0}}{T_{1} - T_{0}}\\ &= 1.0027 - \tfrac{13\overset{h}{.}296006 - 13\overset{h}{.}708275}{-0\overset{h}{.}01291975 - 12.0^h}\\ &= 0.9684\end{align}\)
Der neue halbe Tagbogen, wiederum negativ für den Aufgang, ist nun
\(\begin{align} \cos(15^h\cdot t_1) &= \frac{\sin(h_0) - \sin(\beta_1) \cdot \sin(\delta_1)}{\cos(\beta_1) \cdot \cos(\delta_1)}\\ &=\quad\vdots\quad\quad\vdots\\ &= 0.0559390159\dots \end{align}\)
\(\begin{align} t_1 &= -\frac{\textrm{arccos}(0.0559390159)}{15\frac{\circ}{h}}\\ &= -5\overset{h}{.}786217 \end{align}\)
Analog zu Schritt „0“ erhält man für die verbesserte Aufgangszeit nun
\(\begin{align} T_2 &= T_1 + \frac{t_1 - \tau_1}{\mu_1}\\ &= -0\overset{h}{.}01291975 + \frac{-5\overset{h}{.}786217 - (-5\overset{h}{.}611736)}{0.9684}\\ &= -0\overset{h}{.}19309426 \end{align}\)
Dies entspricht der Uhrzeit vom Vortag um
$24^h -0\overset{h}{.}19309426 = 23\overset{h}{.}806906$, was umgerechnet in Stunden/Minuten/Sekunde dann dem Zeitpunkt
$15.1.2001, 23^h 48^m 23^s$ entspricht.
Schritt 2
Führt man das gesamte Szenario ein weiteres mal durch, erhält man folgende Werte:
\(\begin{align} \Theta_2 &= 7\overset{h}{.}503127\\ JD_2 &= 2451925.45027\\ \alpha_2 &= 13\overset{h}{.}289774\\ \delta_2 &= -2\overset{\circ}{.}474954\\ \tau_2 &= -5\overset{h}{.}786647\\ t_2 &= -5\overset{h}{.}789294\\ T_3 &= -0\overset{h}{.}196209 \end{align}\)
und damit den neuen Zeitpunkt
$T_3 = -0\overset{h}{.}196209$, also umgerechnet $15.1.2001, 23^h 48^m 14^s$.
Ein weiterer Schritt zeigt, dass sich dieser Zeitpunkt nur mehr um $1^s$ ändert. Daher ist die gesuchte Aufgangszeit, gerundet auf ganze Minuten, der $15.1.2001, 23^h 48^m$. Dies gilt für den Längengrad $-15^{\circ}$ östliche Länge. Nimmt man $-10^{\circ}$ östliche Länge, braucht man nur
$\frac{5^{\circ}}{15} = 0.333^{\circ}\;\hat{=}\; 20^m$
zu addieren. Man bekommt dann: $0^h 08^m$ für den 16.1.2001 in Übereinstimmung mit dem Himmelsjahr 2001.
Die Rückrechnung auf das Kalenderdatum mitsamt der Uhrzeit kann natürlich auch über den Julianischen Tag erfolgen.
Numerisches Interpolationsverfahren
Es wird die Höhe $h$ des Mondes im (halb)stündlichen Abstand berechnet, dann kann man den Höhenverlauf als Sinus-Zeitfunktion durch eine Gleichung darstellen: Die quadratische Interpolation.
Aus drei Stützstellen lassen sich die Koeffizienten $a, b$ und $c$ einer Parabel $$y = a \cdot x^2 + b \cdot x + c\tag{15}$$
berechnen, die den Verlauf zwischen den gegebenen Funktionswerten annähert. Man startet dabei mit den folgenden Funktionen für den halben Tagbogen: \[\begin{align} f(t) =&\; \cos(\beta_0)\cdot \cos(\delta)\cdot \cos(15\cdot\tau(t))\\ &+ \sin(\beta_0)\cdot \sin(\delta) − \sin(h_0) \end{align}\tag{16}\]
Abb. 2: Prinzip der Nullstellensuche mit quadratischer Interpolation
Man beginnt für beide Kurven mit den ersten Zeitpunkt $t = 1^h$ bis $t = 24^h$, berechnet den Stundenwinkel $\tau(t)$ als Startwert und ermittelt daraufhin die drei in der Graphik gezeigten Stützpunkte für den gesuchten Zeitpunkt $x$:
| Tabelle 3 | |
|---|---|
| Auf-/Untergang | Resultat |
| $y_{-} = f(t - 1^h)$ | $y_+ = a + b + c$ |
| $y_0 = f(t)$ | $y_0 = c$ |
| $y_{+} = f(t + 1^h)$ | $y_- = a - b + c$ |
Dann bestimmt man $a, b$ und $c$ und damit die beiden Nullstellen der obigen Tagbogen-Funktion. \[\begin{align} a &= \frac{y_+ + y_-}{2} - y_0\\ b &= \frac{y_+ - y_-}{2}\\ c &= y_0 \end{align}\tag{17}\]
Die so gefundenen Parabeln haben für $b^2 \geq 4 \cdot a \cdot c$ die Nullstellen $x_{1,2}$ und die somit gefundenen Zeitpunkte (Mitternachtsgleichung)
$$x_{1,2} = \frac{−b \mp \sqrt{b^2 − 4 \cdot a \cdot c}}{2a}\tag{18}$$
und das Extremum:
$$x_N = -\frac{b}{2 \ a}\tag{19}$$
Werden keine Nullstellen und Extrema auf dem Intervall gefunden, so erhöht oder vermindert man $t$ um $24^h$ und wiederholt den Suchvorgang abermals; gegebenenfalls über einen Zeitraum von drei Tagen (Mond) oder nach Bedarf auch länger (Polarnacht/-tag).
Auf- und Untergangszeit: Hat man die Stützstellen $t_− = t − 1$, $t_0 = t$ , $t_+ = t + 1$ gefunden, so liegt nur eine der beiden Nullstellen $x_1$ oder $x_2$ immer in der Nähe von $t_0$ (kleinerer Absolutwert). Die andere Nullstelle liefert nur sinnlose Werte. Das Extremum $x_N$ hilft dann bei der Bestimmung des Auf- und Untergangszeitpunkts $T_{a,u}$ weiter: Ist $x_N \gt 0$, so liegt der gesuchte Aufgangszeitpunkt $T_a$ vor dem gesuchten Untergangszeitpunkt $T_u$. Ist jedoch $x_N \lt 0$, so liegt der Sachverhalt in umgekehrter Form vor. Es gilt:
$$T_a = t_0 + x_1 \quad \text{und} \quad T_u = t_0 + x_2 \quad \text{falls } x_N > 0\tag{20}$$ $$T_a = t_0 + x_2 \quad \text{und} \quad T_u = t_0 + x_1 \quad \text{falls } x_N < 0\tag{21}$$
Man bekommt die Zeitpunkte in $MOZ$ und muss dann noch auf die Zonenzeit ($MEZ$ oder $MESZ$) umrechnen. Im Falle der Mondbewegung entfällt im Monat ein Aufgangs-, ein Untergangs- und ein Kulminationszeitpunkt. Der kann durch folgende Ausschlusskriterien gefunden werden:
$$T_{a,u} < 0 \quad \text{oder} \quad T_{a,u} > 24\tag{22}$$
Zur Kulmination: Ist $x_E \lt 0$ so hat man ein Maximum und damit den Zeitpunkt $x_{1,2}$ der oberen Kulmination gefunden. Ist jedoch $x_E \gt 0$, so hat man das Minimum und damit die untere Kulmination berechnet, die man nicht braucht: Das Himmelsobjekt hat seinen tiefsten Punkt unter dem Horizont erreicht. Seine Höhe ist dann negativ.
Beispiel 3
Man berechne den Zeitpunkt (in $MEZ$) des Mondaufgangs am 16.1.2001 für den Ort $\lambda_0 = 10^{\circ}\;$Ost und $\beta_0 = 50^{\circ}\;$Nord.
Man berechnet als erstes die Höhe $h$ im einem Intervall von 26 Stunden mit Hilfe von Gleichung (16):
| $t(h)$ | Höhe $h$ [°] |
|---|---|
| $\color{#cc0000}{-1}$ | $\color{#cc0000}{-9.9174564728524164}$ |
| $0$ | $-1.4008879269623948$ |
| $1$ | $+7.6619905974511200$ |
| $2$ | $+16.264024232490367$ |
| $3$ | $+23.966091982009797$ |
| $4$ | $+30.230720083427663$ |
| $5$ | $+34.439308630383543$ |
| $6$ | $+36.030017284660161$ |
| $7$ | $+34.743031979369547$ |
| $8$ | $+30.770848659482951$ |
| $9$ | $+24.639260861006612$ |
| $10$ | $+16.959030561803836$ |
| $11$ | $+8.2681369546535599$ |
| $12$ | $-0.99967795779209334$ |
| $13$ | $-10.481806306675004$ |
| $14$ | $-19.832722193158880$ |
| $15$ | $-28.660280873493534$ |
| $16$ | $-36.452091347905856$ |
| $17$ | $-42.511934105372944$ |
| $18$ | $-46.002569282772313$ |
| $19$ | $-46.256329565749390$ |
| $20$ | $-43.232253621070868$ |
| $21$ | $-37.554964310685151$ |
| $22$ | $-30.076882290628159$ |
| $23$ | $-21.531024404194824$ |
| $\color{#cc0000}{24}$ | $\color{#cc0000}{-1.4008879269623948}$ |
| $\color{#cc0000}{25}$ | $\color{#cc0000}{-3.9230286546594542}$ |
$t(h) = -1^h$ liegt im Vortag ($23$ Uhr), $t(h) = 24^h$ und $t(h) = 25^h$ liegen im nächsten Tag ($0$ Uhr bzw. $1$ Uhr)
Man kann bereits erkennen, zur welcher Uhrzeit der Mond aufgeht. Die Auswahl liefert jedoch das Programm: $t = 1^h$. Jetzt gilt es, die Parabel zu bestimmen. Mit den Parabelkoeffizienten $a, b$ und $c$
$a = -0.23042244468713324$
$b = +8.8324560797263807$
$c = +7.6619905974511200$
bekommt man die $y$-Werte:
$y_- = -1.4008879269623948$
$y_0 = +7.6619905974511200$
$y_+ = +16.264024232490367$
Die Nullstellen ermittelt man mit der Mitternachtsformel (18):
$x_2 = -0.84869064901308278$, $x_1$ ist mit $+39.180269379197370$ zu groß und entfällt somit.
Jetzt muss festgestellt werden, ob man einen Aufgangs- oder Untergangspunkt gefunden hat. Das läuft über das Extremum (Gleichung 19). Mit $x_N = +19.165789365092142$ ist $x_N \gt 0$ und damit hat man den Aufgangzeitpunkt gefunden.
Es gilt: $T_a = t_0 + x_2 = 1^h - 0\overset{h}{.}84869064901308278 = 0\overset{h}{.}151309351 = 00^h 09^m$, in Übereinstimmung mit dem Resultat aus Beispiel 2.
Alternative Version von J. Meeus
J. Meeus geht ebenfalls den Weg über die Interpolation, aber das Ziel sind die äquatorialen Koordinaten des Himmelsobjekts, die über einem kurzen Zeitraum von drei Tagen berechnet werden müssen. Die Vorgehensweise ist in Analogie zum Abschnitt Sonne, Sterne und Planeten. Es folgt nun die Berechnung der geozentrisch - äquatorialen Koordinaten des entsprechenden Himmelskörpers zu folgenden drei Zeitpunkten um 0$^h$ dynamischer Zeit:
\[\begin{align} \alpha_1,& \delta_1 \quad\textsf{am Tag}\quad d - 1^d \quad\textsf{um}\quad 0^h \\ \alpha_2,& \delta_2 \quad\textsf{am Tag}\quad d \quad\textsf{um}\quad 0^h \\ \alpha_3,& \delta_3 \quad\textsf{am Tag}\quad d + 1^d \quad\textsf{um}\quad 0^h \end{align}\]
Mit Hilfe der maßgebenden Koordinaten $\alpha_2$, $\delta_2$ wird über Gleichung (1) der halbe Tagbogen t berechnet. Es gilt mit $\mu_p$ = 1 und den Gleichungen (2), (4) und (5):
\[\begin{split} m_0 &= K\\ m_1 &= K - t\\ m_2 &= K + t \end{split}\tag{23}\]
$m_k$ steht für $m_0$ , $m_1$, $m_2$ und muß zwischen $0^h$ und $24^h$ liegen (Reduktionsfunktion: red($m_k$,$24^h$)). Es wurde bereits oben gezeigt, daß man bei Sonne, Sterne und den Planeten bereits mit $m_1$ den Aufgangszeitpunkt, mit $m_2$ den Untergangszeitpunkt und mit $m_0$ die Kulminationszeit hat. Berechnet man jedoch den Mond, sind zusätzliche Gleichungen nötig. Aus der LMST bestimmt man wieder die lokale Sternzeit $\Theta_k$: $$\Theta_k = LMST + 1.00273790931 \cdot m_k\tag{24}$$
Nun wird die Interpolation der drei Mondpositionen gebraucht: $$y = y_2 + \frac{n}{2}\cdot\left[ y_3 - y_1 + n \cdot (y_1 + y_3 - 2\cdot y_2) \right] \quad\text{mit}\quad n = \frac{m_k}{24^h}\tag{25}$$
Für $y_i$ ist der jeweilige Wert von $\alpha_i$ oder $\delta_i$ einzusetzen. Man erhält dann die interpolierten Koordinaten y = $\alpha$ oder y = $\delta$. Um einen Sprung in der Darstellung von $24^h$ auf $0^h$ zu vermeiden, muss folgende Relation beachtet werden:
Zähle $i = 1$ bis $2$
$\quad$ Falls |$\alpha_{i+1} > \alpha_i$| > $12^h$ dann gilt:
$\qquad$ Falls $\alpha_{i+1} > \alpha_i$ dann gilt:
$\quad\qquad$ $\alpha_i = \alpha_i + 24^h$
$\qquad$ sonst gilt:
$\quad\qquad$ $\alpha_{i+1} = \alpha_{i+1} + 24^h$
$\qquad$ Ende
$\quad$ Ende
Nächstes $i$
Ab hier werden nur noch die interpolierten Koordinaten des Mondes gebraucht. Der Stundenwinkel $\tau$ stammt aus Gleichung (10): $$\tau = \Theta_k - \frac{\alpha}{15^h}\tag{26}$$
Durchgang: $$\Delta m = - \tau\tag{27}$$
Auf-/Untergang: $$\Delta m = \frac{H-h_0}{15^h\cdot\cos(\delta)\cdot\cos(\beta_0)\cdot\sin(15^h\cdot\tau)}\tag{28}$$
Die Höhe $h_0$ stammt aus Tabelle 1. Die Höhe $H$ bekommt man mit: $$\sin(H) = \sin(\beta_0)\cdot\sin(\delta) + \cos(\beta_0)\cdot\cos(\delta) \cdot \cos(15^h\cdot\tau)\tag{29}$$
Der gesuchte Zeitpunkt $T$ ist dann: $$T = m_k + \Delta m\tag{30}$$
Beispiel 4
Man berechne den Zeitpunkt (in $MEZ$) des Mondaufgangs am 16.1.2001 für den Ort $\lambda_0 = 10^{\circ}\;$Ost und $\beta_0 = 50^{\circ}\;$Nord.
Als erstes werden die geozentrisch - äquatorialen koordinaten des Mondes für die drei Zeitpunkte am 15.1., am 16.1 und am 17.1. bestimmt, z.B. mit dem „schneller“ Algorithmus laut dieser Methode:
\(\begin{align} 15.01.2001:\quad \alpha_1 &= 12\overset{h}{.}455588640675865 & \delta_1 = +2\overset{\circ}{.}7180513083004127 \\ 16.01.2001:\quad \alpha_2 &= 13\overset{h}{.}295955922809693 & \delta_2 = -2\overset{\circ}{.}5095094272111229 \\ 17.01.2001:\quad \alpha_3 &= 14\overset{h}{.}116613997835508 & \delta_3 = -7\overset{\circ}{.}4619042104156623 \end{align}\)
Der halbe Tagbogen und die Durchgangszeit $m_0$ wurde ermittelt zu:
\(\begin{align} t &= 5\overset{h}{.}7865382720225993\\ m_0 &= 5\overset{h}{.}9320637476530429 \end{align}\)
Daraus ergibt sich die erste Abschätzung der Aufgangszeit:
$m_1 = 0\overset{h}{.}14552547563044360 = 00^h 08^m 44^s$
Die interpolierten Koordinaten des Erdtrabanten sind:
\(\begin{align} \alpha &= 13\overset{h}{.}300991425177983\\ \delta &= -2\overset{\circ}{.}5403677618275222 \end{align}\)
Der Stundenwinkel $\tau$ und die Höhe $H$ sind:
\(\begin{align} \tau &= -5\overset{h}{.}7911753388363190\\ H &= 6\overset{\circ}{.}5070941042247865 \cdot 10^{-2} \approx 4' \end{align}\)
Die Korrektur $\Delta m$ lautet:
\(\begin{align} \Delta m &= 7\overset{h}{.}0973970892369157 \cdot 10^{-3} \\ &= 00^h 00^m 25\overset{s}{.}6 \end{align}\)
Die Korrektur ist damit sehr klein. Daraus resultiert, daß die Meeus-Variante sehr effektiv ist. Und damit hat man die Aufgangszeit des Erdmondes am 16.1.2001:
\(\begin{align} T &= m_1 + \Delta m\\ T &= 0\overset{h}{.}14552547563044360 + 7\overset{h}{.}0973970892369157 \cdot 10^{-3}\\ &= 0\overset{h}{.}152622872719 = 00^h 09^m 10^s \end{align}\)
in Übereinstimmung mit den Beispielen 2 und 3.
Sichtweite und Kimmtiefe
Diesen beiden Themen ist eine eigene Seite gewidmet.