Inhaltsverzeichnis
Dynamische Zeit und $\Delta T$
Die Weltzeit $UT$ (Universal Time) basiert auf der Rotation der Erde um ihre Achse und bezieht sich auf den Meridian in Greenwich/London. Die $UT$ ist für das zivile Leben und für die astronomischen Berechnungen wichtig, bei denen der lokale Stundenwinkel beteiligt ist. Die Weltzeit wird von den meisten fälschlicherweise als „Greenwich Mean Time“ $GMT$ bezeichnet. In der Astronomie hat die „Mittlere Zeit“ eine genaue Bedeutung. Per Definition wird diese mittlere Zeit vom oberen Meridiandurchgang der mittleren Sonne gemessen. Es ist die bürgerliche Zeit, die um Mitternacht beginnt. Daher unterscheiden sich die $GMT$ und $UT$ um 12 Stunden.
Es gibt aber ein Problem, denn die Erdrotation verlangsamt sich im Laufe der Jahrtausende. Gemeint ist hier die Erdrotation (= Drehung um die eigene Achse), nicht die Erdrevolution (= Bewegung der Erde um die Sonne). Darüber hinaus tritt diese Verlangsamung mit unvorhersehbaren Unregelmäßigkeiten auf. Aus diesem Grund ist die Weltzeit $UT$ keine gleichmäßig verstreichende Zeit. Die Astronomen benötigen jedoch so eine gleichmäßige Zeitskala für ihre genauen Berechnungen (Himmelsmechanik, Umlaufbahnen, Ephemeriden).
Von 1960 bis 1983 wurde in den großen astronomischen Almanachen wie z.B. der Astronomical Ephemeris eine einheitliche Zeitskala verwendet, die als Ephemeridenzeit $ET$ bezeichnet wurde und durch die Gesetze der Himmelsdynamik definiert war: Sie basierte auf den Planetenbewegungen. Im Jahre 1984 wurde die $ET$ durch die dynamische Zeit $TD$ ersetzt, die nun durch Atomuhren definiert wird. Die dynamische Zeit ist sozusagen die Fortführung der Ephemeridenzeit.
Man unterscheidet nun eine baryzentrische dynamische Zeit $TDB$ und eine terrestrische dynamische Zeit $TDT$. Diese Zeiten unterscheiden sich aber um höchstens 0.0017 Sekunden, wobei der Unterschied mit der Bewegung der Erde auf ihrer elliptischen Umlaufbahn um die Sonne zusammenhängt (ein relativistischer Effekt). Die terrestrische dynamische Zeit $TDT$ wird oft abkürzend einfach als Terrestrische Zeit $TT$ bezeichnet. Da dieser sehr kleine Unterschied für die meisten praktischen Zwecke vernachlässigt werden kann, macht man meistens keinen Unterschied zwischen $TDT$ und $TT$ und bezeichnet beide einfach als Dynamische Zeit und nennt sie $TD$. Diese Abkürzung stammt nicht — wie man vermuten könnte — vom französischen „Temps Dynamique“, sondern sollte einfach als $T_{dynamisch}$ gelesen werden.
Weiters unterscheidet sich die Weltzeit $UT$ von der koordinierten Weltzeit $UTC$, bei der ab und zu eine Schaltsekunde an einem vorher festgeleten Zeitpunkt eingefügt wird. Der Unterschied ist aber niemals größer als 0.9 Sekunden.
Es stellt sich also die Frage, mit welcher Zeit man arbeiten soll, wenn man z.B. die Auf- und Untergänge von Sonne und Mond oder Planetenpositionen berechnen will. Im Folgenden soll gezeigt werden, welche Regeln für die Verwendung der Weltzeit und der dynamischen Zeit in astronomischen Berechnungen gelten.
Delta T
Die Differenz zwischen der dynamischen Zeit $TD$ und der Weltzeit $UT$ nennt man im Allgemeinen „Delta T“, es gilt:
$$\Delta T = TD - UT\tag{1}$$
$TD$ = dynamische Zeit
$UT$ = Weltzeit (Universal Time)
Die Autoren O. Montenbruck und T. Pfleger beschreiben es in ihrem Buch Astronomie mit dem Personal Computer so:
- Die Weltzeit dient zur Berechnung der Sternzeit.
- Die dynamische Zeit dient zur Berechnung von Sonnen-, Mond- und Planetenephemeriden.
Die Größe $\Delta T$ ist also eine Korrektur aufgrund der unregelmäßigen Erdrotation. Sie liegt derzeit (Stand 2025) bei ca. 69$^s$ und kann immer nur im Nachhinein bestimmt werden.
$\Delta T$ in astronomischen Berechnungen
Jean Meeus geht in seinem Buch More Mathematical Astronomy Morsels etwas detailierter darauf ein, wie man $\Delta T$ in astronomischen Berechnungen berücksichtigt, was nachstehend weiter erläutert wird. Der vollständige Text ist in diesem Paper zu finden.
Unsere Uhren beziehen sich auf die Weltzeit $UT$ und gehen in Bezug auf die gleichmäßige dynamische Zeit $TD$ allmählich nach, da die Rotation der Erde um ihre Achse im Laufe der Jahrtausende langsamer wird. Tatsächlich scheinen astronomische Ereignisse bei Verwendung der $UT$-Skala früher aufzutreten als in einer gleichmäßigen Zeitskala vorhergesagt.
„Wenn meine Uhr um fünf Minuten langsamer geht, scheint ein Zug, der tatsächlich um 19:50 Uhr ankommt, um 19:45 Uhr anzukommen.“
Leider ist es hier nicht ganz so einfach. Man könnte denken, dass es ausreicht die Ergebnisse in Weltzeit $UT$ zu erhalten, wenn man zuerst die Größe $TD$ vernachlässigt, d.h. $TD = 0$ setzt, dann die Berechnungen durchführt, um danach die Größe $TD$ von den erhaltenen Zeiten wieder zu subtrahieren. Dies ist jedoch nicht immer so!
Im Jahr 1999 entsprach $\Delta T = 64$ Sekunden. In der nachstehenden Tabelle 1 sind sechs Ereignisse aus dem Jahr 1999 aufgeführt. In der vierten Spalte werden die Zeitpunkte in $UT$ so berechnet, als würde $\Delta T = 0$ sein, d.h. $UT = TD$. Die $UT$-Zeiten in der fünften Spalte wurden hingegen mit dem korrekten Wert $\Delta T = 64$ Sekunden berechnet:
| Tabelle 1 | |||||
|---|---|---|---|---|---|
| Nr. | Datum 1999 | Ereignis | $UT$ für $\Delta T = 0$ | $UT$ für $\Delta T = 64^{s}$ | Differenz |
| 1 | 21. Juni | Sommerbeginn | 19:50:11 | 19:49:07 | $−64^{s}$ |
| 2 | 28. Juli | Mondfinsternis, 1. Kontakt | 10:23:04 | 10:22:00 | $−64^{s}$ |
| 3 | 25. August | Perihelzeit des periodischen Kometen Giclas | 03:10:08 | 03:09:04 | $−64^{s}$ |
| 4 | 26. Mai | Meridiandurchgang von Spica in Greenwich | 21:09:12 | 21:09:12 | $0^{s}$ |
| 5 | 18. September | Meridiandurchgang des Mondes in Greenwich | 18:35:05 | 18:35:07 | $+2^{s}$ |
| 6 | 11. August | Sonnenfinsternis in Greenwich | |||
| Erster Kontakt: | 09:05:05 | 09:03:44 | $-81^{s}$ | ||
| Letzter Kontakt: | 11:41:43 | 11:40:14 | $-89^{s}$ | ||
Auf den ersten Blick mag es überraschend erscheinen, dass die Werte in der letzten Spalte nicht gleich sind. Bei den ersten drei Ereignissen liegt die $UT$-Zeit erwartungsgemäß 64 Sekunden vor der $TD$-Zeit. Für Ereignis Nr. 4 hat eine Wertänderung von $\Delta T$ jedoch überhaupt keine Auswirkung auf den Zeitpunkt in der $UT$-Skala. Für das fünfte Ereignis ist der Unterschied gering und positiv. Für das letzte Ereignis sind die Differenzen wieder negativ, aber im absoluten Wert deutlich größer als $\Delta T$ selbst. Was ist der Grund für diese Differenzen?
Ereignisse 1, 2 und 3
Die ersten drei Ereignisse der Tabelle 1 beziehen sich nicht auf die Ausrichtung der Erdkugel im Weltraum und haben daher nichts mit der Rotation der Erde zu tun. Per Definition tritt die Sommersonnenwende ein, wenn die wahre geozentrische Länge $\lambda_{\odot}$ der Sonne (d.h. berechnet unter Einbeziehung der Auswirkungen von Aberration und Nutation) genau 90° beträgt. 1999 fand die Sonnenwende am 21. Juni um 19:50:11 $TD$ statt. Hier subtrahiert man also einfach $\Delta T$, um den Moment in $UT$ zu erhalten, nämlich 19:49:07. Soweit kein Problem.
Gleiches gilt für das zweite und dritte Ereignis. Unter Verwendung der klassischen Regel von 1/50 für die Vergrößerung der Erdumbra und unter der Annahme, dass diese genau kreisförmig ist, zeigt eine strenge Berechnung, dass bei der Mondfinsternis vom 28. Juli 1999 der erste Kontakt des Mondes mit der Umbra um 10:23:04 $TD$ stattfand. Wieder subtrahiert man $\Delta T$ oder 64 Sekunden, um die $UT$-Zeit zu erhalten.
Gleiches gilt auch für den vorhergesagten Zeitpunkt des Durchgangs des periodischen Kometen Giclas durch sein Perihel. Laut dem Minor Planet Circular Nr. 27082 war dieser Zeitpunkt der 25.13204 August 1999 $TD$, was umgerechnet den 25. August 1999, 03:10:08 $TD$ bedeutet.
Für alle astronomischen Phänomene, die nicht mit der Erdrotation (um die eigene Achse) zusammenhängen, gilt dieselbe Regel: $$UT = TD - \Delta T\tag{2}$$
- die Phänomene der Monde des Jupiter
- die geozentrischen Phasen eines Merkurtransits über die Sonnenscheibe
- die Zeiten der Äquinoktien und Solstitien
- die Zeiten der Mondphasen
- der Moment einer Opposition des Mars, usw.
Ereignis 4
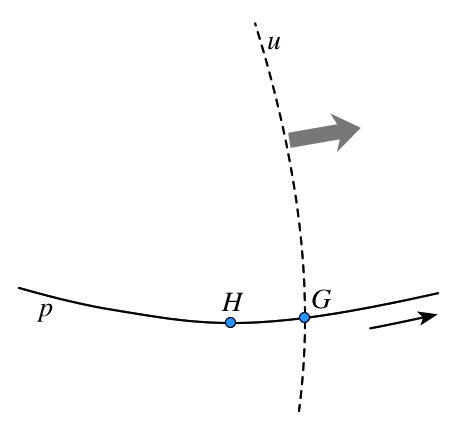
 Abb. 1: Meridiandurchgang Stern
Nun schaut man sich Ereignis Nr. 4 der Tabelle 1 an. Die Abb.1 zeigt die Erde von oben. $N$ ist der Nordpol, $S$ die Richtung zu einem Stern, z.B. Spica. Dargestellt ist der Breitenkreis von Greenwich/London von oben (nicht der Äquator!). Der Ort des Beobachters, hier Greenwich, bewegt sich zusammen mit der Rotation der Erde. Wenn der Beobachter bei $G$ ankommt, durchläuft Stern den Meridian. Angenommen, $\Delta T$ ist zuerst 0. In diesem Fall kommt Greenwich am 26. Mai 1999 um 21:09:12 $TD$ = 21:09:12 $UT$ bei Punkt $G$ an, und Spica durchläuft in diesem Moment den Meridian.
Abb. 1: Meridiandurchgang Stern
Nun schaut man sich Ereignis Nr. 4 der Tabelle 1 an. Die Abb.1 zeigt die Erde von oben. $N$ ist der Nordpol, $S$ die Richtung zu einem Stern, z.B. Spica. Dargestellt ist der Breitenkreis von Greenwich/London von oben (nicht der Äquator!). Der Ort des Beobachters, hier Greenwich, bewegt sich zusammen mit der Rotation der Erde. Wenn der Beobachter bei $G$ ankommt, durchläuft Stern den Meridian. Angenommen, $\Delta T$ ist zuerst 0. In diesem Fall kommt Greenwich am 26. Mai 1999 um 21:09:12 $TD$ = 21:09:12 $UT$ bei Punkt $G$ an, und Spica durchläuft in diesem Moment den Meridian.
Der tatsächliche Wert von $\Delta T$ beträgt jedoch 64 Sekunden. Da sich die tatsächliche Erdrotation mit Bezug auf eine Erde mit gleichmäßiger Rotation um 64 Sekunden verspätet, ist Greenwich um 21:09:12 $TD$ immer noch bei Punkt $H$. Erst nach weiteren 64 Sekunden wird Greenwich bei Punkt $G$ sein. In Wirklichkeit erfolgt also Spicas Transit (in der Zeitskala $TD$) 64 Sekunden später als es der Fall wäre, wenn $\Delta T = 0$ wäre. Um die $TD$-Zeit in $UT$ umzuwandeln, muss die Größe $\Delta T$ subtrahiert werden, sodass die Transitzeit in der $UT$-Skala
$$\textrm{21:09:12} + 64^{s} - 64^{s} $
beträgt, was wiederum 21:09:12 $UT$ ergibt. Folglich werden in der $UT$-Skala die Zeiten der Transite von Sternen nicht durch die Größe $\Delta T$ beeinflusst. Sternentransits treten tatsächlich später in der gleichförmigen $\Delta T$-Skala auf, aber unsere $UT$-Uhren verzögern sich um denselben Betrag.
Um genau zu sein, werden die $UT$-Zeiten von Sternentransits durch $\Delta T$ doch beeinflusst, jedoch nur durch einen extrem kleinen Betrag, da die Auswirkungen von Aberration und Nutation während des kurzen Zeitintervalls von $\Delta T$ sehr geringfügig variieren! Dies darf aber in vielen Fällen vernachlässigt werden.
Ereignis 5
Für Transite des Mondes haben wir fast die gleiche Situation, außer dass sich der Mond während des Zeitintervalls $\Delta T$ ein wenig um die Erde weiter bewegt. Die Abb.2 zeigt erneut den Breitenkreis von Greenwich von oben. Angenommen, $\Delta T = 0$. In diesem Fall kommt Greenwich am 18. September 1999 um 18:35:05 Uhr $TD$ = 18:35:05 $UT$ in Punkt $G$ an, und der Mond durchläuft in diesem Moment den Meridian. Wie zuvor ist Greenwich um 18:35:05 $TD$ immer noch bei Punkt $H$, da der tatsächliche Wert von $\Delta T$ nicht 0, sondern 64 Sekunden beträgt. Erst nach weiteren 64 Sekunden erreicht Greenwich Punkt $G$. Während dieser 64 Sekunden bewegt sich der Mond aber von $M$ nach $M'$ weiter, sodass sich die Erde sich noch ein wenig weiter von $G$ nach $K$ drehen muss, bevor sich der Mond genau auf dem Meridian in Greenwich befindet. Dies dauert in diesem Fall weitere 2 Sekunden. Und schließlich müssen wir die Größe $\Delta T$ subtrahieren, um von $TD$ nach $UT$ zu konvertieren. Die Transitzeit in $UT$ ist somit
$$\text{18:35:05} + 64^{s} + 2^{s} - 64^{s}$$
oder 18:35:07, was erklärt, warum der Mondtransit 2 Sekunden später in der $UT$-Skala stattfindet, verglichen mit dem Fall, wenn $\Delta T = 0$ wäre. In der gleichförmigen $TD$-Skala erfolgt der Transit daher 66 Sekunden später.
Ereignis 6
Zu guter Letzt noch zum 6. und letzten Punkt der obigen Tabelle 1. Die Abb.2 zeigt einen Teil der Erdoberfläche, wobei die Linie $p$ am Breitengrad von Greenwich sei. Wieder nehmen wir zuerst an, dass $\Delta T = 0$ ist. Die gestrichelte Linie ist der Rand des Mondhalbschattens (Penumbra) auf der Erdoberfläche. Ihre Position $u$ wird in dem Moment dargestellt, in dem sie Greenwich = Punkt $G$ erreicht. Das ist der Moment des ersten Kontakts bei einer Sonnenfinsternis.
Es sei $t$ dieser Moment in der Skala $TD$. Aufgrund der täglichen Rotation der Erde bewegt sich entlang in Richtung des dünnen Pfeils. Die Kante des Halbschattes bewegt sich ebenfalls nach Osten in Richtung des dicken Pfeils, jedoch mit einer höheren Geschwindigkeit als $G$, sodass der Halbschatten Punkt $G$ überholt. Im Jahr 1999 beträgt $\Delta T = 64^{s}$. Daher hat Greenwich zum Zeitpunkt $t$ den Punkt $G$ noch nicht erreicht, sondern befindet sich noch bei Punkt $H$. Mit anderen Worten, der erste Kontakt erfolgt tatsächlich einige Sekunden vor $t$.
Für die Sonnenfinsternis vom 11. August 1999 in Greenwich beträgt diese Differenz 17 Sekunden, und die Entfernung $\overline{HG}$ beträgt 19 Kilometer. Um den Zeitpunkt in der Zeitskala von $UT$ zu erhalten, müssen wir noch 64 Sekunden subtrahieren. Daher beträgt der Gesamtunterschied $-17^{s}-64^{s} = -81^{s}$ Sekunden, wie in der Tabelle 1 angegeben.
Da die Geschwindigkeit des Halbschattens des Mondes in Bezug auf den Beobachter von Ort zu Ort variiert, beträgt der oben erwähnte Unterschied nicht für alle Orte $−81^{s}$. Es gibt sogar einen Unterschied zwischen dem ersten und dem letzten Kontakt, wie in der letzten Zeile der Tabelle 1 zu sehen ist. Diese Differenzen von $−81^{s}$ bzw. $−89^{s}$ Sekunden sind das Ergebnis einer genauen Berechnung unter Verwendung der sogenannten Besselschen Elemente der betreffenden Finsternis mittels einschlägiger Formeln.
Für Interessierte: Der 5 Millennium Canon of Solar Eclipses von Fred Espenak und Jean Meeus kann hier gefunden werden. Dieser Canon enthält 11898 Sonnenfinsternisse im Zeitraum [−1999 bis +3000].
Praktische Tipps
- Man führt für Ereignisse, die nicht mit der Erdrotation zusammenhängen, die Berechnung in der einheitlichen Skala der dynamischen Zeit $TD$ durch und subtrahiert dann die Größe $\Delta T$ von den erhaltenen Zeiten, um sie in $UT$ umzuwandeln.
Beispiele dazu wurden bereits weiter oben erwähnt. - Für die Zeiten des Aufgangs, des Meridiandurchgangs und des Untergangs eines Himmelskörpers wird die lokale Sternzeit $\theta$ verwendet. Diese wird direkt aus der $UT$ ermittelt, daher sollte die Berechnung in dieser Zeitskala durchgeführt werden. Für einen bestimmten Zeitpunkt in $UT$ sollte dann aber die Position des Himmelskörpers für den Zeitpunkt $UT + \Delta T$ dynamische Zeit berechnet werden. Die resultierenden Aufgangszeiten usw. werden direkt in $UT$ ausgegeben, sodass keine weitere Korrektur mit $\Delta T$ erforderlich ist.
- Für die lokalen Umstände einer Sonnenfinsternis oder einer Sternbedeckung durch den Mond werden im Allgemeinen die sogenannten Besselschen Elemente verwendet. Diese Elemente sind in der $TD$-Skala angegeben. Es genügt hier zu erwähnen, dass bei der Berechnung des lokalen Stundenwinkels der Sonne (oder eines Sterns) eine Korrektur von $-1.002738\cdot \Delta T$ angewendet wird, das Sternzeitäquivalent von $\Delta T$. Die endgültigen $TD$-Zeiten der Kontakte usw. werden dann durch Subtrahieren der Größe $\Delta T$ in $UT$ umgewandelt.
Werte für $\Delta T$
| Tabelle 2: Werte für $\Delta T$ aus historischen Aufzeichnungen | ||
|---|---|---|
| Jahr | $\Delta T$ in Sek. | Standardfehler $\sigma$ in Sek. |
| -500 | 17190 | 430 |
| -400 | 15530 | 390 |
| -300 | 14080 | 360 |
| -200 | 12790 | 330 |
| -100 | 11640 | 290 |
| 0 | 10580 | 260 |
| 100 | 9600 | 240 |
| 200 | 8640 | 210 |
| 300 | 7680 | 180 |
| 400 | 6700 | 160 |
| 500 | 5710 | 140 |
| 600 | 4740 | 120 |
| 700 | 3810 | 100 |
| 800 | 2960 | 80 |
| 900 | 2200 | 70 |
| 1000 | 1570 | 55 |
| 1100 | 1090 | 40 |
| 1200 | 740 | 30 |
| 1300 | 490 | 20 |
| 1400 | 320 | 20 |
| 1500 | 200 | 20 |
| 1600 | 120 | 20 |
| 1700 | 9 | 5 |
| 1750 | 13 | 2 |
| 1800 | 14 | 1 |
| 1850 | 7 | <1 |
| 1900 | -3 | <1 |
| 1950 | 29 | <0.1 |
| Tabelle 3: Werte für $\Delta T$ aus direkten Messungen | |||
|---|---|---|---|
| Jahr | $\Delta T$ (Sek.) | 5-Jahres Diff. (Sek.) | Mittlere 1-Jahr Diff. (Sek.) |
| 1955.0 | +31.1 | — | — |
| 1960.0 | +33.2 | 2.1 | 0.42 |
| 1965.0 | +35.7 | 2.5 | 0.50 |
| 1970.0 | +40.2 | 4.5 | 0.90 |
| 1975.0 | +45.5 | 5.3 | 1.06 |
| 1980.0 | +50.5 | 5.0 | 1.00 |
| 1985.0 | +54.3 | 3.8 | 0.76 |
| 1990.0 | +56.9 | 2.6 | 0.52 |
| 1995.0 | +60.8 | 3.9 | 0.78 |
| 2000.0 | +63.8 | 3.0 | 0.60 |
| 2005.0 | +64.7 | 0.9 | 0.18 |
| Tabelle 4: Jüngere Werte für $\Delta T$ (Sek.) | |||
|---|---|---|---|
| Jahr | IERS Bulletin B data | USNO MICA v2.2.2 | IERS Sub-bureau |
| 2010.0 | — | +66.1 | +65.5 |
| 2012.0 | +66.6 | +66.6 | +65.8 |
| 2014.0 | +67.3 | +67.7 | +66.1 |
| 2016.0 | +68.1 | +68.5 | +66.4 |
| 2018.0 | +69.0 | +69.6 | +66.7 |
| 2020.0 | +69.4 | +70.7 | +67.0 |
Vorhersage für $\Delta T$ laut IERS Prediction Center
Dieses Daten werden vierteljährlich vom IERS aktualisiert. Wie man sieht weichen die Vorhersagen von der „Berechnung“ ab, der Wert von $\Delta T$ scheint sich zur Zeit (2024) weniger schnell zu entwickeln.
| Tabelle 5 | ||
|---|---|---|
| Jahr | $\Delta T = TD-UT$ (Sek.) | Fehler (Sek.) |
| 2022.50 | 69.29 | 0.031 |
| 2022.75 | 69.21 | 0.021 |
| 2023.00 | 69.21 | 0.019 |
| 2023.25 | 69.20 | 0.021 |
| 2023.50 | 69.18 | 0.024 |
| 2023.75 | 69.11 | 0.027 |
| 2024.00 | 69.11 | 0.033 |
| 2024.25 | 69.11 | 0.043 |
| 2024.50 | 69.10 | 0.056 |
| 2024.75 | 69.03 | 0.070 |
| 2025.00 | 69.04 | 0.088 |
| 2025.25 | 69.07 | 0.109 |
| 2025.50 | 69.06 | 0.133 |
| 2025.75 | 69.01 | 0.159 |
| 2026.00 | 69.05 | 0.189 |
| 2026.25 | 69.09 | 0.223 |
| 2026.50 | 69.11 | 0.257 |
| 2026.75 | 69.09 | 0.291 |
| 2027.00 | 69.14 | 0.327 |
| 2027.25 | 69.21 | 0.367 |
| 2027.50 | 69.26 | 0.408 |
| 2027.75 | 69.26 | 0.446 |
| 2028.00 | 69.34 | 0.486 |
| 2028.25 | 69.44 | 0.525 |
| 2028.50 | 69.51 | 0.566 |
| 2028.75 | 69.54 | 0.603 |
| 2029.00 | 69.63 | 0.637 |
| 2029.25 | 69.75 | 0.672 |
| 2029.50 | 69.83 | 0.711 |
| 2029.75 | 69.87 | 0.742 |
| 2030.00 | 69.97 | 0.768 |
| 2030.25 | 70.08 | 0.794 |
| 2030.50 | 70.17 | 0.823 |
| 2030.75 | 70.21 | 0.849 |
| 2031.00 | 70.32 | 0.871 |
| 2031.25 | 70.42 | 0.891 |
| 2031.50 | 70.51 | 0.913 |
| 2031.75 | 70.53 | 0.926 |
| 2032.00 | 70.62 | 0.937 |
| 2032.25 | 70.72 | 0.952 |
| 2032.50 | 70.82 | 0.975 |
| 2032.75 | 70.86 | 1.000 |
| 2033.00 | 70.98 | 1.000 |
| 2033.25 | 71.10 | 1.000 |
| 2033.50 | 71.20 | 1.000 |
| 2033.75 | 71.25 | 1.000 |
Grafischer Verlauf
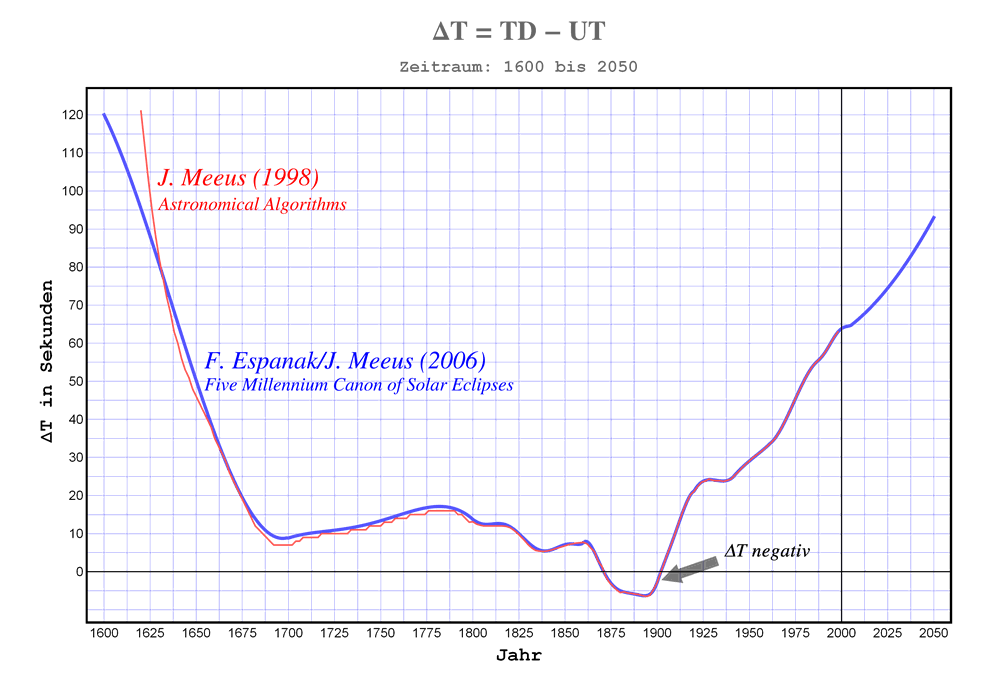 Abb. 4: Vergleichsgraphen für ΔT
Abb. 4: Vergleichsgraphen für ΔT
Die Abb.4 zeigt den Verlauf von $\Delta T$ im Zeitraum von 1600-2050, wobei für Daten in der Zukunft extrapoliert wurde. Die rote Linie zeigt die Daten von J. Meeus bis zum Jahr 1998, wie sie in seinen Astronomical Algorithms dargestellt sind. Die blaue Linie ist eine Berechnung von F. Espanak und J. Meeus, wobei für einzelne Zeitabschnitte ein Polynom-Fit vorgenommen wurde. Die einzelnen Polynome für diese Darstellung können auf dieser Seite nachgelesen werden.
Berechnung mit Polynomen
Die Autoren L. Morrison und F. R. Stephenson entwickelten eine Berchnungsmöglichkeit für die Größe von $\Delta T$ für einen relativ großen Zeitraum. Genauere Messungen für $\Delta T$ gibt es erst ab den 1950er Jahren, die Werte für den Zeitraum ab ca. 1600 sind ebenfalls Messwerten der damaligen Zeit zu verdanken, wenngleich diese Messungen nicht so genau waren wie heute.
Für noch frühere Zeiten kann $\Delta T$ aus historischen Aufzeichnungen abgeleitet werden. Insbesondere wurden hunderte von Sonnen- und Mondfinsternisbeobachtungen in frühen Annalen, Manuskripten und Kanonen Europas, des Nahen Ostens und Chinas aufgezeichnet. Trotz ihrer relativ geringen Präzision stellen diese Daten die einzige Grundlage für den Wert von $\Delta T$ vor dem 17. Jahrhundert dar. In den Jahrhunderten nach der Einführung des Teleskops (um ca. 1609 n.Chr.) wurden tausende hochwertiger Beobachtungen von Sternbedeckungen durch den Mond gemacht. Die Anzahl und Genauigkeit dieser Zeitmessungen nahm vom 17. bis zum 20. Jahrhundert zu und lieferte wertvolle Daten für die Bestimmung von $\Delta T$. Eine detaillierte Analyse dieser mit kubischen Splines angepassten Messungen für $\Delta T$ von $-500$ bis $+1950$ ist in Tabelle 2 bereits dargestellt.
Unter Verwendung der $\Delta T$-Werte, die aus historischen Aufzeichnungen und aus direkten Beobachtungen abgeleitet wurden, wurde von den Autoren eine Reihe von Polynomausdrücken erstellt, um die Auswertung von $\Delta T$ für jeden Zeitpunkt im Intervall $-1999$ bis $+3000$ zu vereinfachen.
Mit einer gegebenen Jahreszahl sowie dem Monat definiert man das „Dezimaljahr“ $J$ wie folgt:
$$ J = \textsf{Jahr} + \frac{(\textsf{Monat} - 0.5)}{12}\tag{3}$$
Dies ergibt $J$ jeweils für die Monatsmitte, was angesichts der Genauigkeit der bekannten Werte von $\Delta T$ ausreichend genau ist. Die folgenden Polynomausdrücke können nun verwendet werden, um den Wert von $\Delta T$ (in Sekunden) über den Zeitraum von $-1999$ bis $3000$ zu berechnen.
| Tabelle 6 | ||
|---|---|---|
| Zeitraum | Polynom für $\Delta T$ [s] | Parameter |
| vor $-500$ | $\Delta T = -20 + 32\cdot u^2$ | $\large u = \frac{J - 1820}{100}$ |
| $-500$ bis $500$ | \(\begin{align} \Delta T &= 10583.6\\ &- 1014.41\cdot u\\ &+ 33.78311\cdot u^2\\ &- 5.952053\cdot u^3\\ &- 0.1798452\cdot u^4\\ &+ 0.022174192\cdot u^5\\ &+ 0.0090316521\cdot u^6 \end{align}\) | $\large u = \frac{J}{100}$ |
| $500$ bis $1600$ | \(\begin{align} \Delta T &= 1574.2\\ &- 556.01\cdot u\\ &+ 371.23472\cdot u^2\\ &+ 0.319781\cdot u^3\\ &- 0.8503463\cdot u^4\\ &- 0.005050998\cdot u^5\\ &+ 0.0083572073\cdot u^6 \end{align}\) | $\large u = \frac{J - 1000}{100}$ |
| $1600$ bis $1700$ | \(\begin{align} \Delta T &= 120\\ &- 0.9808\cdot u\\ &- 0.01532\cdot u^2\\ &+ \frac{1}{7129}\cdot u^3 \end{align}\) | $u = J - 1600$ |
| $1700$ bis $1800$ | \(\begin{align} \Delta T &= 8.83\\ &+ 0.1603\cdot u\\ &- 0.0059285\cdot u^2\\ &+ 0.00013336\cdot u^3\\ &- \frac{1}{1174000}\cdot u^4\\ \end{align}\) | $u = J - 1700$ |
| $1800$ bis $1860$ | \(\begin{align} \Delta T &= 13.72\\ &- 0.332447\cdot u\\ &+ 0.0068612\cdot u^2\\ &+ 0.0041116\cdot u^3\\ &- 3.7436\cdot 10^{-4}\cdot u^4\\ &+ 1.21272\cdot 10^{-5}\cdot u^5\\ &- 1.699\cdot 10^{-7}\cdot u^6\\ &+ 8.75\cdot 10^{-10}\cdot u^7 \end{align}\) | $u = J - 1800$ |
| $1860$ bis $1900$ | \(\begin{align} \Delta T &= 7.62\\ &+ 0.5737\cdot u\\ &- 0.251754\cdot u^2\\ &+ 0.01680668\cdot u^3\\ &- 0.0004473624\cdot u^4\\ &- \frac{1}{233174}\cdot u^5 \end{align}\) | $u = J - 1860$ |
| $1900$ bis $1920$ | \(\begin{align} \Delta T &= -2.79\\ &+ 1.494119\cdot u\\ &- 0.0598939\cdot u^2\\ &+ 0.0061966\cdot u^3\\ &- 0.000197\cdot u^4 \end{align}\) | $u = J - 1900$ |
| $1920$ bis $1941$ | \(\begin{align} \Delta T &= 21.20\\ &+ 0.84493\cdot u\\ &- 0.076100\cdot u^2\\ &+ 0.0020936\cdot u^3 \end{align}\) | $u = J - 1920$ |
| $1941$ bis $1961$ | \(\begin{align} \Delta T &= 29.07\\ &+ 0.407\cdot u\\ &- \frac{1}{233}\cdot u^2\\ &+ \frac{1}{2547}\cdot u^3 \end{align}\) | $u = J - 1950$ |
| $1961$ bis $1986$ | \(\begin{align} \Delta T &= 45.45\\ &+ 1.067\cdot u\\ &- \frac{1}{260}\cdot u^2\\ &+ \frac{1}{718}\cdot u^3 \end{align}\) | $u = J - 1975$ |
| $1986$ bis $2005$ | \(\begin{align} \Delta T &= 63.86\\ &+ 0.3345\cdot u\\ &- 0.060374\cdot u^2\\ &+ 0.0017275\cdot u^3\\ &+ 0.000651814\cdot u^4\\ &+ 2.373599\cdot 10^{-5}\cdot u^5 \end{align}\) | $u = J - 2000$ |
| $2005$ bis $2050$ | \(\begin{align} \Delta T &= 62.92\\ &+ 0.32217\cdot u\\ &+ 0.005589\cdot u^2 \end{align}\) | $u = J - 2000$ |
| $2050$ bis $2150$ | \(\begin{align} \Delta T &= -20 + 32\cdot \left(\frac{J-1820}{100}\right)^2\\ &- 0.5628\cdot (2150 - J) \end{align}\) | — |
| nach $2150$ | \(\begin{align} \Delta T &= -20 + 32\cdot u^2 \end{align}\) | $\large u = \frac{J - 1820}{100}$ |
Die Extrapolation von $\Delta T$ für zukünftige Zeiten ist hier mit Vorsicht zu genießen. Derzeit (2024) scheint sich der Wert von $\Delta T$ langsamer zu entwickeln als durch die Polynome berechnet wird.
Beispiel
Für Mitte März 1982 soll die Position von Mars um $\textrm{22:00}\;MEZ$ berechnet werden. Dazu wird die Größe $\Delta T$ benötigt.
$UT = MEZ - 1^{h} = \textrm{21:00}$
$J = 1982 + \frac{3 - 0.5}{12} = 1982.208333$
Mit dem Datumsbereich $1961$ bis $1986$ aus der Tabelle hat man dann den Parameter
$u = 1982.20833 - 1975 = 7.208333$
Damit ergibt sich für $\Delta T$ dann
\(\begin{align} \Delta T &= 45.45\\ &+ 1.067\cdot 7.208333\\ &- \frac{7.208333^2}{260}\\ &- \frac{7.208333^3}{718}\\ &= 52\overset{s}{.}4198 \end{align}\)
Die Planetenposition muss nun für den Zeitpunkt in dynamischer Zeit berechnet werden, nämlich
$TD = UT + \Delta T = \textrm{21:00} + 52^{s} = \textrm{21:00:52}$