Inhaltsverzeichnis
Finsternisse
Mit den Finsternissen wird ein sehr reizvolles Himmelsphänomen vorausberechnet, deren Schatten- und Lichtspiele bis heute die Menschen berührt. Eine Sonnenfinsternis hat man, wenn der Mond vor der Sonne steht und sie bedeckt, bei einer Mondfinsternis wandert der Mond durch den Erdschatten. Ebenfalls zu den Finsternissen gehören die Sternbedeckungen, die Transite der unteren Planeten vor der Sonne und die sehr seltenen Planetenbedeckungen.
Vorausberechnung
Eine erste Abschätzung der Finsternistermine ist durch die Neu- und Vollmondphasen möglich. Liegt dann die ekliptikale Breite bei kleiner $1^{\circ}$, kann man mit einer Finsternis rechnen. Die Feinheiten werden anhand zweier Vorgehensweisen präsentiert.
Meeus
Meeus beginnt mit dem Delaunay Argument $F = l - \Omega$ und der Phasenummer $k$:
| Tabelle 1 | |
|---|---|
| \[\begin{array}{lll} & |F - 360^{\circ}\cdot k| < 13.9^{\circ} & \textsf{Finsternis sicher} \\ 13.9^{\circ} < & |F - 360^{\circ}\cdot k| < 21^{\circ} & \textsf{Finsternis wahrscheinlich} \\ & |F - 360^{\circ}\cdot k| > 21^{\circ} & \textsf{keine Finsternis} \end{array}\] | |
Es folgt: $$F' = F - 0\overset{\circ}{.}02665\cdot \sin(\Omega)\tag{1}$$ $$A' = 299\overset{\circ}{.}77 + 0.107408 \cdot k - 0\overset{\circ}{.}09173 \cdot T^2\tag{2}$$
Man nehme die mittleren Bahnelemente $m, M, F$ und $\Omega$ und den julianischen Tag $JDE_0$ aus dem Kapitel über die Mondphasen und addiere die folgenden Reihenentwicklungen dazu:
| Tabelle 2 | |
|---|---|
| Sonnenfinsternisse: | $\Delta JDE_{SF} = -0\overset{d}{.}4075\cdot \sin(m) + 0\overset{d}{.}1721\cdot E \cdot \sin(M)$ |
| Mondfinsternisse: | $\Delta JDE_{MF} = - 0\overset{d}{.}4065\cdot \sin(m) + 0\overset{d}{.}1727\cdot E \cdot \sin(M)$ |
mit $E$ als der auf $1$ normierten, numerischen Exzentrizität der Erdbahn (siehe Mondposition nach Meeus)
\[\begin{align} \Delta JDE_0 =& +0\overset{d}{.}0161\cdot \sin (2\cdot m)\\ & -0\overset{d}{.}0097\cdot \sin (2\cdot F')\\ & +0\overset{d}{.}0073\cdot E\cdot \sin (m - M)\\ & -0\overset{d}{.}0050\cdot E\cdot \sin (m + M)\\ & -0\overset{d}{.}0023\cdot \sin (m - 2\cdot F')\\ & +0\overset{d}{.}0021\cdot E\cdot \sin (2\cdot M)\\ & +0\overset{d}{.}0012\cdot \sin (m + 2\cdot F')\\ & +0\overset{d}{.}0006\cdot E\cdot \sin (2\cdot m + M)\\ & -0\overset{d}{.}0004\cdot \sin (3\cdot m)\\ & -0\overset{d}{.}0003\cdot E\cdot \sin (M + 2\cdot F')\\ & +0\overset{d}{.}0003\cdot \sin (A')\\ & -0\overset{d}{.}0002\cdot E\cdot \sin (M - 2\cdot F)\\ & -0\overset{d}{.}0002\cdot E\cdot \sin (2\cdot m - M)\\ & -0\overset{d}{.}0002\cdot \sin (\Omega) \end{align}\tag{3}\]
Alles zusammen ergeben die Finsternistermine nach Meeus:
| Tabelle 3 | |
|---|---|
| Sonnenfinsternis: | $JDE_{SF} = JDE_0 + \Delta JDE_{SF} + \Delta JDE_0$ |
| Mondfinsternis: | $JDE_{MF} = JDE_0 + \Delta JDE_{MF} + \Delta JDE_0$ |
Montenbruck/Pfleger
Montenbruck & Pfleger beginnen mit dem Delaunay Argument $D = l - L$ und der Phasennummer $k$.
\[\begin{align} \Delta\lambda &=\;0^{\circ}\\ &= \lambda_M - \lambda_S\\ &= l - L + \Delta l - \Delta L - 90^{\circ}\cdot k \Rightarrow\\ 0^{\circ} &= D + \Delta l - \Delta L - 90^{\circ}\cdot k\\ &= D_0 + D_1\cdot T + D_2\cdot T^2 + \Delta l - \Delta L - 90^{\circ}\cdot k \end{align}\tag{4}\]
Bei einer Sonnenfinsternis ($k=0$) und einer Mondfinsternis ($k=2$) muss $\Delta\lambda = 0^{\circ}$ sein. Jetzt muss der Zeitpunkt $T$ gefunden werden, an dem $\Delta\lambda$ verschwindet. Dies geschieht mit dem Pegasus Verfahren:
$$T_2 = T_1 - \frac{T_1 − T_0}{\Delta\lambda(T_1) - \Delta\lambda(T_0)}\cdot \Delta\lambda(T_1)\tag{5}$$
Man startet mit einem Intervall $[T_0;T_1]$ in dem $\Delta\lambda$ ein Vorzeichenwechsel hat und bestimmt dann $T_2$.
Gilt $\Delta\lambda(T_2)\cdot \Delta\lambda(T_1) \leq 0$, ersetze $T_0$ und $\Delta\lambda(T_0)$ durch $T_1$ und $\Delta\lambda(T_1)$.
Gilt $\Delta\lambda(T_2)\cdot \Delta\lambda(T_1) > 0$, ersetze $T_0$ und $\Delta\lambda(T_0)$ durch $T_1$ und $\dfrac{\Delta\lambda(T_0)\cdot\Delta \lambda(T_1)}{\Delta\lambda(T_1) + \Delta\lambda(T_2)}$.
Die geozentrische Breite $\beta$ kann auch eine Hilfe bei der Suche der Finsternistermine sein:
| Tabelle 4 | ||||
|---|---|---|---|---|
| Mondphase | Länge | Breite | Finsternisart | Sichtbarkeit |
| Sonnenfinsternis Neumond | $|L - \Omega| < 9\overset{\circ}{.}45$ | $|\beta| < 0^{\circ} 52' 20''$ | zentral | sicher |
| $|L - \Omega| < 12\overset{\circ}{.}06$ | $|\beta| < 1^{\circ} 02' 36''$ | zentral | wahrscheinlich | |
| $|L - \Omega| < 15\overset{\circ}{.}38$ | $|\beta| < 1^{\circ} 24' 33''$ | partiell | sicher | |
| $|L - \Omega| < 18\overset{\circ}{.}45$ | $|\beta| < 1^{\circ} 34' 50''$ | partiell | wahrscheinlich | |
| $|L - \Omega| > 18\overset{\circ}{.}45$ | $|\beta| > 1^{\circ} 34' 50''$ | keine | nicht möglich | |
| Mondfinsternis Vollmond | $|L^* - \Omega| < 3\overset{\circ}{.}93$ | $|\beta| < 0^{\circ} 21' 50''$ | total | sicher |
| $|L^* - \Omega| < 6\overset{\circ}{.}17$ | $|\beta| < 0^{\circ} 32' 14''$ | total | wahrscheinlich | |
| $|L^* - \Omega| < 9\overset{\circ}{.}64$ | $|\beta| < 0^{\circ} 53' 24''$ | partiell | sicher | |
| $|L^* - \Omega| < 12\overset{\circ}{.}30$ | $|\beta| < 1^{\circ} 03' 50''$ | partiell | wahrscheinlich | |
| $|L^* - \Omega| < 15\overset{\circ}{.}69$ | $|\beta| < 1^{\circ} 26' 15''$ | Halbschatten | sicher | |
| $|L^* - \Omega| < 18\overset{\circ}{.}83$ | $|\beta| < 1^{\circ} 36' 43''$ | Halbschatten | wahrscheinlich | |
| $|L^* - \Omega| > 18\overset{\circ}{.}83$ | $|\beta| > 1^{\circ} 36' 43''$ | keine | nicht möglich | |
mit $L^* = L +180^{\circ}$. Die Tabelle stammt aus dem Buch Spherical Astronomy von R. Green.
Die stündliche Berechnung
Nachdem der Finsternistermin $JDE_{SF}$ oder $T$ genähert berechnet wurde, werden nun die stündlichen äquatorialen Sonnen- und Mondkoordinaten 24 Stunden vor und nach dem gefundenen Finsternistermin ermittelt. Die stündlichen Änderungen der Sonnen- bzw. Mondkoordinaten sind dann $\Delta\alpha_S$, $\Delta\delta_S$ bzw. $\Delta\alpha_M$, $\Delta\delta_M$.
Geometrie
Fundamentalebene
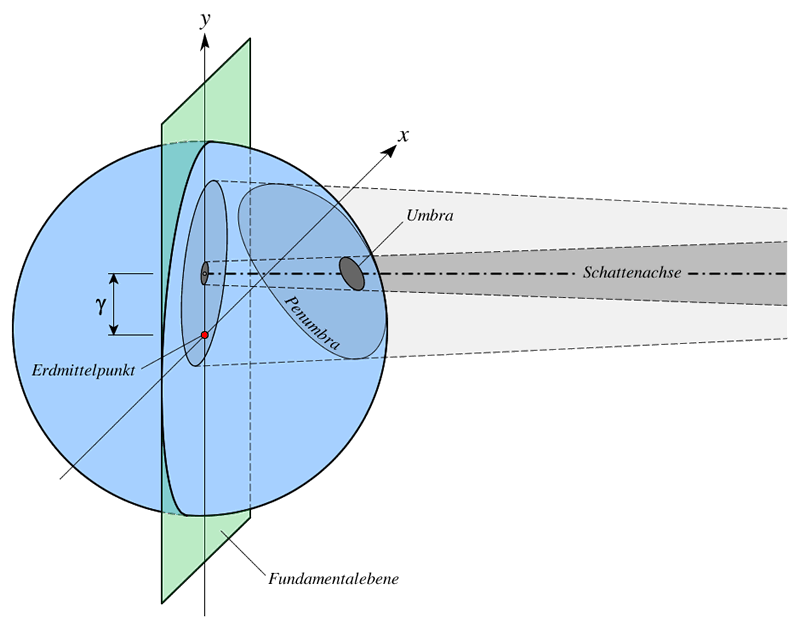
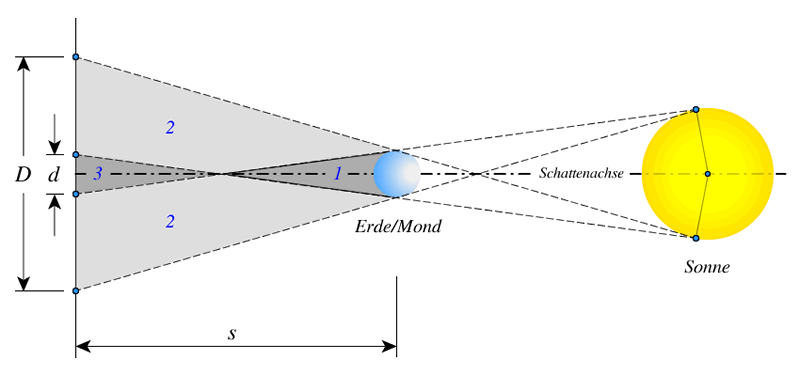 Abb. 1: Umbra und Penumbra, Schattenachse
Abb. 1: Umbra und Penumbra, Schattenachse
Die sonnenabgewandte Verbindungslinie (Abb.1 oben) wird Schattenachse genannt. Sie steht senkrecht auf der Fundamentalebene, die die Erde in ihrem Mittelpunkt durchschneidet (Abb.2 unten). Die zugehörigen $x$- und $y$-Achsen spannen die Fläche der Fundamentalebene auf, während die $z$-Achse in Richtung der Schattenachse zeigt. Die $x$-Achse liegt in der Schnittlinie zur Äquatorebene.
Man führt jetzt die Einheitsvektoren $\Delta \cdot \vec{e}$ ein und unterscheidet zwischen den beiden Lichtphänomenen. Das nachfolgende Schema stammt aus Meeus und Montenbruck/Pfleger.
Geozentrisch - äquatoriale Koordinaten der Sonne: $$\vec{r}_S = \Delta_S \cdot \left( \begin{align} &\cos(\delta_S) \cdot \cos(\alpha_S) \\ &\cos(\delta_S) \cdot \sin(\alpha_S) \\ &\sin(\delta_S) \\ \end{align}\right) = \Delta_S \cdot \vec{e}_S\tag{6}$$ Geozentrisch - äquatoriale Koordinaten des Erdmondes: $$\vec{r}_M = \Delta_M \cdot \left( \begin{align} &\cos(\delta_M) \cdot \cos(\alpha_M) \\ &\cos(\delta_M) \cdot \sin(\alpha_M) \\ &\sin(\delta_M) \\ \end{align}\right) = \Delta_M \cdot \vec{e}_M\tag{7}$$ Sonnenfinsternisse: $$s = - \vec{r}_M\cdot\vec{e}_S - \sqrt{s_0^2 + R_E^2 - r_M^2}\tag{8}$$ mit $$\vec{e}_S = \frac{\vec{r}_M - \vec{r}_S}{|\vec{r}_M - \vec{r}_S|}\tag{9}$$ Mondfinsternisse: \[\begin{align} s &= - \vec{r}_M\cdot\vec{e}_M - \sqrt{s_0^2 + R_E^2 - r_M^2}\\ &= s_0 - \sqrt{\Delta}\\ &= s_0 - \sqrt{R_E^2 - \gamma^2} \end{align}\tag{10}\]
mit $$\vec{e}_M = \frac{\vec{r}_S - \vec{r}_M}{|\vec{r}_S - \vec{r}_M|}\tag{11}$$
Der Wert $\gamma$ = $\sqrt{r_M^2 - s_0^2}\;$ (Abb.2 oben) ist laut J. Meeus der Abstand der Schattenachse vom Erdmittelpunkt (Gamma-Wert), wobei $s_0$ anschaulich die Entfernung des Mondes von der Fundamentalebene ist.
$\sqrt{\Delta}$ ist der Abstand der verfinsterten Erdoberfläche von der Fundamentalebene. Das Argument der Wurzel muss positiv sein, sonst läuft die Schattenachse an der Erde vorbei. Die Koordinaten des Kernschattens auf der Erde sind dann:
Sonnenfinsternisse: \[\begin{align} \vec{r} &= \vec{r}_M + s \cdot \vec{e}\\ &= \vec{r}_M + \left(- \vec{r}_M\cdot\vec{e}_S - \sqrt{s_0^2 + R_E^2 - r_M^2}\right) \cdot \vec{e}_S \end{align}\tag{12}\]
Mondfinsternisse: \[\begin{align} \vec{r} &= \vec{r}_M + (s_0 - \sqrt{\Delta}) \cdot \vec{e}\\ &= \vec{r}_M + \left(- \vec{r}_M\cdot\vec{e}_M - \sqrt{s_0^2 + R_E^2 - r_M^2}\right) \cdot \vec{e}_M \end{align}\tag{13}\]
Kern- und Halbschatten
Es existieren zwei Kategorien der Schatten: Der Halbschatten und der Kernschatten. (Abb.3 unten). In einer Ebene vertikal zur Schattenachse hinter der Erde oder Mond in einem Abstand $s$ betragen die Durchmesser $d(s)$ der Kernschatten und $D(s)$ der Halbschatten (Montenbruck & Pfleger).
 Abb. 3: Halbschatten und Kernschatten
Abb. 3: Halbschatten und Kernschatten
Sonnenfinsternisse: \[\begin{align} d_S(s) &= 2 \cdot R_S\cdot \left(\dfrac{s}{r_{SM}}\right) - 2 \cdot R_M\cdot \left(1 + \dfrac{s}{r_{SM}}\right) \\ D_S(s) &= 2 \cdot R_S\cdot \left(\dfrac{s}{r_{SM}}\right) + 2 \cdot R_M\cdot \left(1 + \dfrac{s}{r_{SM}}\right) \end{align}\tag{14}\]
Mondfinsternisse: \[\begin{align} d_M(s) &= 2 \cdot R_S \left(\dfrac{s}{r_{SE}}\right) - 2 \cdot R_E \left(1 + \dfrac{s}{r_{SE}}\right) \\ D_M(s) &= 2 \cdot R_S \left(\dfrac{s}{r_{SE}}\right) + 2 \cdot R_E \left(1 + \dfrac{s}{r_{SE}}\right) \end{align}\tag{15}\]
Man berechnet jetzt den Mondabstand von der Sonne $r_{SM}$
$$r_{SM} = \sqrt{R^2 + \Delta_M^2 - 2 \cdot R \cdot \Delta_M\cdot \cos(\eta)}\tag{16}$$
mit der Mondelongation $\eta$ und dem modifizierten Mondabstand $\Delta_M = \frac{\Delta}{149\,597\,870.662}$. $d(s)$ ist so gehalten, dass $d$ negativ bei einer totalen Finsternis und positiv bei einer partiellen Finsternis wird.
Sichtbarkeit der Finsternisse
Jetzt wird die Finsternisart bestimmt. Partiell, total oder keine Finsternis. Bei einer totalen Finsternis muss noch zwischen einer zentralen und nichtzentralen Finsternis unterschieden werden.
Es gilt: $D_0 = D(s_0)$ und $d_0 = d(s_0)$.
| Tabelle 5 | ||
|---|---|---|
| Finsternisart | Sichtbarkeit der Sonnenfinsternisse | Sichtbarkeit der Mondfinsternisse |
| zentral: | $R_E > |\gamma|$ | $R_M > |\gamma|$ |
| dezentral: | $R_E + \dfrac{|d_0|}{2} > |\gamma| > R_E$ | $R_M + \dfrac{|d_0|}{2} > |\gamma| > R_M$ |
| partiell: | $R_E + \dfrac{D_0}{2} > |\gamma| > R_E + \dfrac{|d_0|}{2}$ | $R_M + \dfrac{D_0}{2} > |\gamma| > R_M + \dfrac{|d_0|}{2}$ |
| keine: | $|\gamma| > R_E + \dfrac{D_0}{2}$ | $|\gamma| > R_M + \dfrac{D_0}{2}$ |
Wieder sind $d$ die Durchmesser der Kernschatten und $D$ der Halbschatten:
Sonnenfinsternisse: $$\dfrac{d_S}{2} = \pi_M - \pi_S + \dfrac{\varnothing_S}{2} - \dfrac{\varnothing_M}{2}\tag{17}$$ $$\dfrac{D_S}{2} = \pi_M - \pi_S + \dfrac{\varnothing_S}{2} + \dfrac{\varnothing_M}{2}\tag{18}$$
Mondfinsternisse: $$\dfrac{d_M^\pm}{2} = 1.02 \cdot \left(0.99834 \cdot \pi_M + \pi_S - \dfrac{\varnothing_S}{2}\right) \pm \dfrac{\varnothing_M}{2}\tag{19}$$ $$\dfrac{D_M}{2} = 1.02 \cdot \left(0.99834 \cdot \pi_M + \pi_S + \dfrac{\varnothing_S}{2}\right) + \dfrac{\varnothing_M}{2}\tag{20}$$
$d^{+}$ ist partielle Phase und $d^{-}$ die totale Phase. Die Parallaxen der Sonne $\pi_S$ und des Mondes $\pi_M$ stammen von hier und hier.
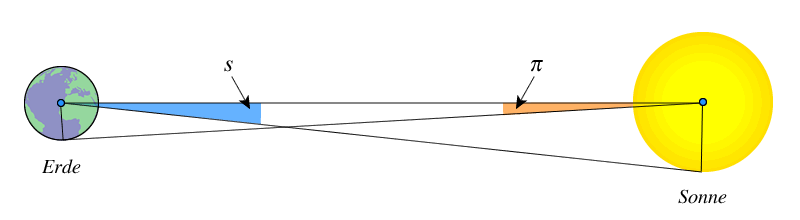 Abb. 4: Parallaxe Erde-Sonne (nicht maßstäblich)
Abb. 4: Parallaxe Erde-Sonne (nicht maßstäblich)
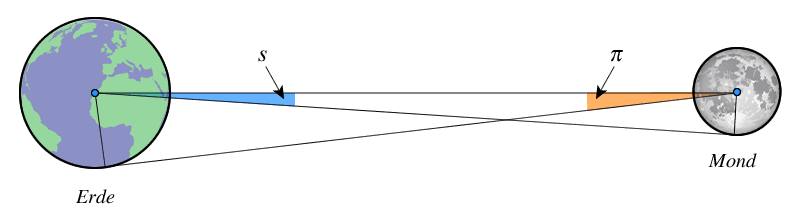 Abb. 5: Parallaxe Erde-Mond (nicht maßstäblich)
Abb. 5: Parallaxe Erde-Mond (nicht maßstäblich)
Die Durchmesser der Sonne $\varnothing_S$ und des Mondes $\varnothing_M$ findet man in diesem Kapitel. Der Faktor $1.02$ berücksichtigt den Vergrößerungseffekt der Erdatmosphäre. Es gilt:
| Tabelle 6: Sonnenfinsternisse: | |
|---|---|
| keine Sonnenfinsternis: | $\sigma \gt \dfrac{D_S}{2}$ |
| partielle Phase: | $\sigma \lt \dfrac{D_S}{2}$ und $\sigma \gt \dfrac{d_S}{2}$ |
| totale Phase: | $\sigma \lt \dfrac{d_S}{2}$ |
| Tabelle 7: Mondfinsternisse: | |
|---|---|
| keine Mondfinsternis: | $\sigma \gt \dfrac{D_M}{2}$ |
| Halbschattenphase: | $\sigma \lt\dfrac{D_M}{2}$ und $\sigma \gt \dfrac{d_M^+}{2}$ |
| partielle Phase: | $\sigma \lt \dfrac{d_M^+}{2}$ und $\sigma \gt \dfrac{d_M^-}{2}$ |
| totale Phase: | $\sigma \lt \dfrac{d_M^-}{2}$ |
Finsternisdauer
Montenbruck/Pfleger/Roth
Ausgangszeitpunkt $T$ ist die Sonnenfinsternis und Mondfinsternis des Mondes in den Gleichungen der Mondphasenberechnung:
\[\begin{align} T_S &= 24^h \cdot JDE_{SF} = JDE_N\\ \\ T_M &= 24^h \cdot JDE_{MF} = JDE_V \end{align}\tag{21}\]
Sonnenfinsternis
Die Schattenachse schneidet zwei gegebene Orte auf der Erdoberfläche mit den geografischen Koordinaten $\vec{r}(\lambda_0, \beta_0$) zum Zeitpunkt $t$ und $\vec{r}'(\lambda_0', \beta_0')$ zum Zeitpunkt $t' = t + \Delta t$. $\Delta t$ ist die Zeitdifferenz, in der der Mondschatten über den Erdglobus wandert. In demselben Zeitraum dreht sich die Erde um den Betrag
$$w = \frac{360^{\circ}}{1436^m} \cdot \Delta t\tag{22}$$
weiter. Das Stück muss nochmals addiert werden. Es gilt dann für den Ort $\vec{r}$' zum Zeitpunkt $t' = t + \Delta t$: $\;\lambda_0' + w$.
Der Weg, den der Kernschatten auf der Erdoberfläche relativ zur Eigendrehung der Erde zurücklegt, ist dann:
$$\Delta\vec{r} = \vec{r}''(\lambda_0' + w, \beta_0') - \vec{r}(\lambda_0, \beta_0)\tag{23}$$
Mit Hilfe der Vektors $\vec{e}_s$ kann man dann die Dauer der Sonnenfinsternis $\tau$ berechnen:
$$\tau = \frac{|d_S(s)| \cdot \Delta t}{\sqrt{\Delta\vec{r}^2 - \Delta\vec{r}\cdot\vec{e}_s}}\tag{24}$$
Aus der obigen Gleichung für $\Delta\lambda$ in der Vorausberechnung ergibt sich der Zeitpunkt der Finsternismitte:
$$t = T_M - \frac{36525}{D_1}\cdot \big[D(T_M) + \Delta l(T_M) - \Delta L(T_M)\big]\tag{25}$$
Montenbruck & Pfleger empfehlen hier eine kurze Iteration mit $T_M = t$ und dann erneutes Einsetzen mit dann finalem $t$. Als Finsternisbeginn wählt man daraufhin $t_{D-} = t - \frac{\tau}{2}$ und damit für das Finsternisende $t_{D+} = t + \frac{\tau}{2}$. Dies unterscheidet noch nicht zwischen der partiellen Phase und der eigentlichen, sehr kurzen Totalität. Für die partielle Phase setze man $D_S(s)$ statt $d_S(s)$ in die obige Gleichung ein. Eine andere Möglichkeit ist die Einführung von $f(t)$:
$$f(t) = (x_M - \xi)^2 + (y_M - \eta)^2 - L^2 = \gamma^2 - L^2\tag{26}$$
Wieder kann durch das Pegasus Verfahren die Nullstelle $t$ (d.h. der Zeitpunkt des Ein- und Austritts aus der Finsternis) gefunden werden, an der $f(t) = 0$ gilt. $L$ ist der Radius des Halb- oder Kernschattenkegels auf der Fundamentalebene und $\xi$, $\eta$ sind die karthesisch-geographischen Koordinaten des Beobachters.
Mondfinsternis
Dieser Bereich hat das Handbuch für Sternfreunde als Quelle. Zur Bestimmung der Mondopposition in Rektaszension nimmt man noch einmal das Pegasus Verfahren von Montenbruck & Pfleger, diesmal für die Rektaszension und Deklination aus den geozentrisch-äquatorialen Koordinaten der Sonne $\alpha_S$, $\delta_S$ und des Mondes $\alpha_M$, $\delta_M$.
Man bildet den solaren Gegenpunkt mit der Reduktions- und Rundungsfunktion
\[\begin{align} \alpha_G &= \textrm{red}(\alpha_S + 12^h,\;24^h) \\ \delta_G &= - \delta_S \end{align}\tag{27}\]
und dann die Differenz daraus:
$$\alpha_M - \alpha_G = \Delta\alpha = 0^{\circ}\tag{28}$$.
Für Mondfinsternisse muss diese Differenz zu einem gesuchten Zeitpunkt $T$ Null sein. Als Startzeit kann man $T_0 = T_M - 0.5^h$ und $T_1 = T_M + 0.5^h$ nehmen. Die Suche nach der gewünschten Zeit $T$ wird wieder mit dem Pegasus Verfahren gelöst:
$$T_2 = T_1 - \frac{T_1 - T_0} {\Delta \alpha (T_1) - \Delta \alpha(T_0)} \cdot \Delta \alpha(T_1)\tag{29}$$
Man startet mit diesem Zeitintervall [$T_0;\; T_1$] in dem ein Vorzeichenwechsel von $\Delta\alpha$ stattfindet. Das Pegasus Verfahren ist nur ein Austauschverfahren.
$$\Delta \alpha(T_2) \cdot \Delta \alpha(T_1) \leq 0\tag{30}$$
ersetze $t_0$ und $\Delta \alpha(T_0)$ durch $t_1$ und $\Delta \alpha(T_1)$
$$\Delta \alpha(T_2) \cdot \Delta \alpha(T_1) \gt 0\tag{31}$$
ersetze $t_0$ und $\Delta \alpha(T_0)$ durch $t_1$ und $\frac{\Delta \alpha(T_0)\cdot \Delta \alpha(T_1)}{\Delta \alpha(T_1) + \Delta \alpha(T_2)}$
Nun berechne man die stündlichen, äquatorialen Sonnen- und Mondkoordinaten um das gefundene $T = T_n$ herum. Weiter geht es mit dem Handbuch für Sternfreunde: Die stündlichen Änderungen der Sonnen- und Mondkoordinaten sind dann $\Delta\alpha_S$, $\Delta\delta_S$ und $\Delta\alpha_M$, $\Delta\delta_M$.
Der Zeitpunkt der Finsternismitte ist dann:
$$t = T_M - \frac{\delta_S + \delta_M}{\Delta\delta_S + \Delta\delta_M}\tag{32}$$
Mit der lokalen Neigung der Mondbahn $i$ gegen die Ekliptik am Mondort (quadrantenkorrekte Darstellung beachten)
$$i = \textrm{arctan2}\left(-\frac{\Delta \delta_S + \Delta \delta_M}{15^h\cdot \cos(\delta_S)\cdot (\Delta \alpha_M - \Delta \alpha_S)}\right)\tag{33}$$
und dem kleinsten Abstand $\rho$ des Mondes von dem Kernschattenzentrum zur Finsternismitte $$\rho = (\delta_S + \delta_M)\cdot\cos(i)\tag{34}$$
kann man die Finsternisdauer nun berechnen. Der Beginn ($-$) und das Ende ($+$) der Halbschattenfinsternis $t_D$ ist (mit $t_G$ als der Gesamtdauer):
\[\begin{align} t_{D\mp} &= t \mp \frac{\sqrt{D_M^2 - \rho^2}}{\Delta \delta_S + \Delta \delta_M}\cdot \sin(i) \\ \tau &= t_{D+} - t_{D-} \end{align}\tag{35}\]
Der Beginn ($-$), das Ende ($+$) und die Gesamtdauer $\tau$ der Totalität erhält man mit dem Austausch von $D_M$ gegen $d_M^-$. Tauscht man ebenso $D_M$ gegen $d_M^+$, so erhält man die Gesamtdauer $\tau$ für die partielle Phase.
Meeus
Meeus geht da einen alternativen und einfacheren Weg. Mit den Hilfswerten $P$ und $Q$ wird der Abstand $\gamma$ der Schattenachse vom Erdmittelpunkt ermittelt. Die Einheit ist in Erdäquatorradien und $E$ ist die normierte num. Exzentrizität der Erdbahn:
\[\begin{align} P =&+ 0.2070 \cdot E \sin(M)\\ &+ 0.0097 \cdot E \sin(2 \cdot M)\\ &- 0.0392 \cdot E \sin(m)\\ &+ 0.0116 \cdot E \sin(2 \cdot m)\\ &- 0.0073 \cdot \sin(m + M)\\ &+ 0.0067 \cdot E \sin(m - M)\\ &+ 0.0118 \cdot \sin(2 \cdot F') \\\\ Q = &+ 5.2207 - 0.0048 \cdot E \cos(M)\\ &+ 0.0020 \cdot E \cos(2 \cdot M)\\ &- 0.3299 \cdot E \cos(m)\\ &- 0.0060 \cdot E \cos(m + M)\\ &+ 0.0041 \cdot E \cos(m - M) \end{align}\tag{36}\]
$$\gamma = \big[P \cdot \cos(F') + Q \cdot \sin(F')\big]\cdot (1 - 0.0048 \cdot \lvert\cos(F')\rvert)\tag{37}$$
$\gamma$ ist positiv für eine nördliche Passage vom Erd- bzw. Mondmittelpunkt, negativ für eine südliche Passage. $u$ ist der Radius des Kernschattenkegels des Mondes auf der Erde (in Erdäquatorradien) und wird jetzt zur Berechnung des Erdkernschattens auf dem Mond herangezogen:
\[\begin{align} u =& + 0.0059 \\ & - 0.0182 \cdot \cos(m) \\ & + 0.0048 \cdot E \cdot \cos(M) \\ & + 0.0004 \cdot \cos(2 \cdot m) \\ & - 0.0005 \cdot \cos(M + m) \end{align}\tag{38}\]
Sonnenfinsternis
Die Radien (in Erdäquatorradien) der Halb- und Kernschatten des Mondes haben folgende Größen:
| Tabelle 8 | |
|---|---|
| Halbschatten: | $D_S = 0.5461 + u$ |
| Kernschatten: | $d_S = u$ |
| totale Sonnenfinsternis: | $|\gamma| < 0.9972$ |
| partielle Sonnenfinsternis: | $0.9972 < |\gamma| < 1.5433 + u$ |
| treifende Sonnenfinsternis: | $0.9972 < |\gamma| < 1.026$ |
| nichtzentrale oder ringförmige Sonnenfinsternis: | $0.9972 < |\gamma| < 0.9972 + |u|$ |
| keine Sonnenfinsternis: | $|\gamma| > 1.5433 + u$ |
Bei einer streifenden Sonnenfinsternis tangiert ein Kernschattenteil die Erdoberfläche (in der Regel an den Polen), während die Schattenachse die Erde nicht erreicht oder sogar verfehlt. Es gilt weiter:
| Tabelle 9 | |
|---|---|
| totale Sonnenfinsternis: | $u < 0$ |
| ringförmige Sonnenfinsternis: | $u > 0.0047$ |
| ringförmig-totale oder ringförmige Sonnenfinsternis: | $0 < u < 0.0047$ |
$$\omega = 0.00464\cdot \sqrt{1 - \gamma^2} \gt 0\tag{39}$$
stellt man fest, ob eine zentrale Sonnenfinsternis ringförmig-total ($u \lt \omega$) oder nur ringförmig ($u\geq \omega$) ist. Man sollte den Wert |$\gamma$| auf $1.0$ oder $1.005$ vergrößern, um alle möglichen totalen Finsternisse zu erfassen.
Mondfinsternis
Die Radien (in Erdäquatorradien) der Halb- und Kernschattenkegel der Erde haben im Mondabstand folgende Größen (Handbuch für Sternfreunde):
$$\text{Halbschatten: } D_M = 1.2848 + u\tag{40}$$ $$\text{Kernschatten: } d_M = 0.7403 - u\tag{41}$$
Die halbe Dauer der partiellen Phase $P$, der totalen Phase $T$ und der Halbschattenphase $H$ der Kernschattenfinsternis berechnet man folgenderweise:
\[\begin{align} H &= 1.5573 + u\\ P &= 1.0128 - u\\ T &= 0.4678 - u\\ n &= 0\overset{\circ}{.}5458 + 0\overset{\circ}{.}04\cdot \cos(m) \end{align}\tag{42}\]
Dann ist die halbe Dauer $\frac{\tau}{2}$ in Minuten:
| Tabelle 10 | |
|---|---|
| Halbschatten: | $\frac{\tau_h}{2} = \frac{60}{n}\cdot \sqrt{H^2 - \gamma^2}$ |
| partiell: | $\frac{\tau_p}{2} = \frac{60}{n}\cdot \sqrt{P^2 - \gamma^2}$ |
| total: | $\frac{\tau_t}{2} = \frac{60}{n}\cdot \sqrt{T^2 - \gamma^2}$ |
- Die Halbschattenfinsternisse (auch penumbrale Finsternisse genannt) können nicht visuell beobachtet werden, auch die Kontakte nicht. Nur bei tiefen Halbschattenfinsternissen ist am Mondrand eine schwache Abschattung zu sehen.
- Bei streifenden Sonnenfinsternissen berührt ein Teil des Kernschattens die Erdoberfläche (in der Regel an den Polen), während die Schattenachse die Erde nicht erreicht oder sogar verfehlt.
- Der Erdschatten weicht mit größer werdender Distanz immer deutlicher von seiner Kreisform ab. Die Abplattung der Erde macht sich schon im Mondabstand bemerkbar. Die Abplattung des Kernschattens liegt dann von 1:214 bis 1:102.
Besselsche Elemente
Zur Berechnung der lokalen Umstände einer Sonnenfinsternis benötigt man die Koordinaten der Sonne $\vec{r}_S$ und des Mondes $\vec{r}_M$ in Bezug auf die Fundamentalebene (kurz: die geozentrisch-äquatorialen Koordinaten der Schattenachse, auch Besselsche Elemente genannt, Explanatory Supplement). Es gilt:
\[\begin{align} g \cdot \cos(d) \cdot \cos(a) = & x = \cos(\delta_S) \cdot \cos(\alpha_S) - \frac{\sin(\pi_S)}{\sin(\pi_M)} \cdot \cos(\delta_M) \cdot \cos(\alpha_M) \\ g \cdot \cos(d) \cdot \sin(a) = & y = \cos(\delta_S) \cdot \sin(\alpha_S) - \frac{\sin(\pi_S)}{\sin(\pi_M)} \cdot \cos(\delta_M) \cdot \sin(\alpha_M) \\ g \cdot \sin(d) = & z = \sin(\delta_S) - \frac{\sin(\pi_S)}{\sin(\pi_M)} \cdot \sin(\delta_M) \end{align}\tag{43}\]
mit dem geozentrischen Sonnenabstand $\Delta_S = R = 1$ und $$\frac{\Delta_M}{\Delta_S} = \frac{\sin(\pi_S)}{\sin(\pi_M)}\tag{44}$$
und $\pi_S$, $\pi_M$ als die Sonnen- und Mondparallaxen $$\sin(\pi_S) = \frac{R_E}{\Delta_S} \quad \textsf{und} \quad \sin(\pi_M) = \frac{R_E}{\Delta_M}\tag{45}$$
wieder mit dem modifizierten Mondabstand $\Delta_M$.
$g$ hat die Einheit 1 AE und diesen Wert erhält man mit
$$g = \sqrt{x^2 + y^2 + z^2}.\tag{46}$$
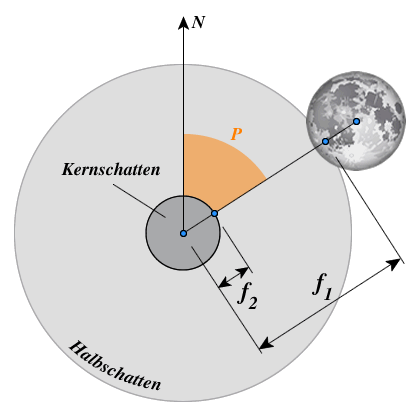
Damit gilt für die halben Öffnungswinkel der Schattenkegel $f_1$ und $f_2$:
$$\text{Halbschattenkegel: }\sin(f_1) = \frac{R_S + R_M}{g \ R_S}\tag{47}$$ $$\text{Kernschattenkegel: } \sin(f_2) = \frac{R_S - R_M}{g \ R_S}\tag{48}$$
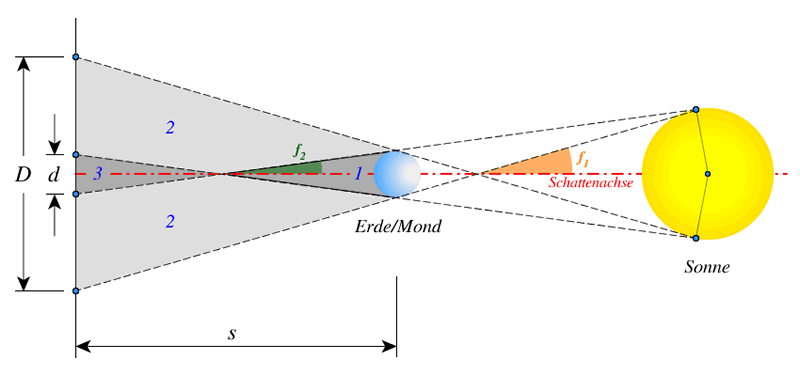 Abb. 6: Halbschatten- und Kernschattenkegel in einer SoFi
Abb. 6: Halbschatten- und Kernschattenkegel in einer SoFi
Die Radien der Schattenkegel auf der Fundamentalebene sind $L_1$ für den Halbschattenkegel und $L_2$ für den Kernschattenkegel beim Beobachter sind nun einfach zu ermitteln: $$L_1 = \frac{R_M}{R_E} + (z - R_E \cos(\beta_0)) \ \tan(f_1)\tag{49}$$ $$L_2 = \frac{R_M}{R_E} - (z + R_E \cos(\beta_0)) \ \tan(f_2)\tag{50}$$
Die $z$-Komponente der auf die Fundamentalebene bezogenen Mondkoordinaten $\vec{r}_M$ lautet:
\(\begin{align} z &= g \cdot \frac{\sin(\pi_S)}{\sin(\pi_M)} \cdot \big[\cos(\delta_M) \cdot \cos(\alpha_M) \cdot \cos(d) \cdot \cos(a) \\ &+ \cos(\delta_M) \cdot \sin(\alpha_M) \cdot \cos(d) \cdot \sin(a) \\ &+ \sin(\delta_M) \cdot \sin(d)\big] \end{align}\tag{51}\)
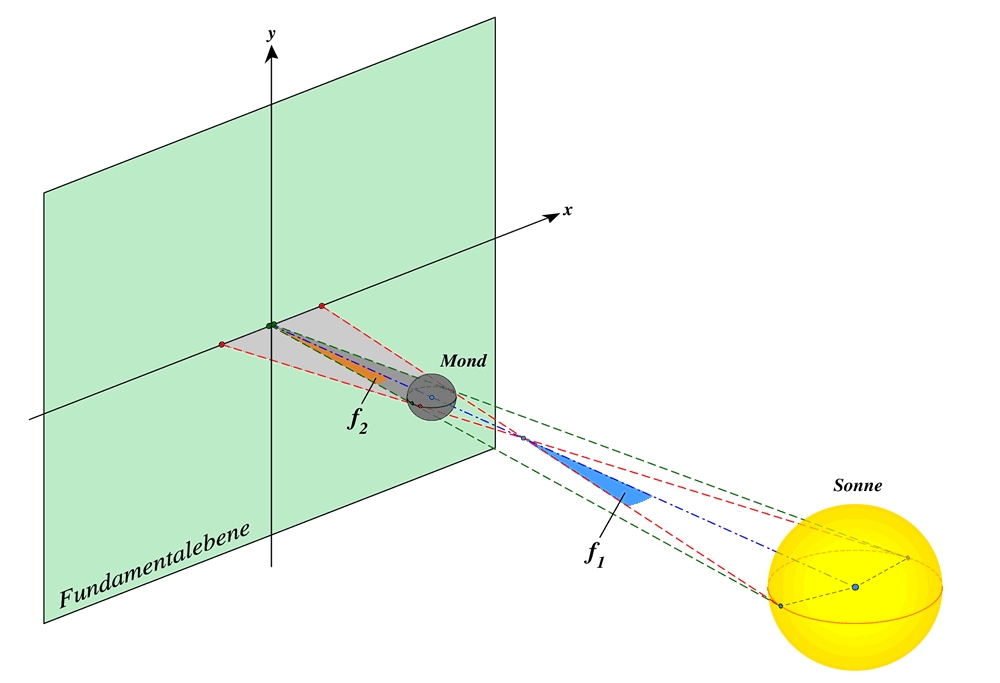 Abb. 1: Halbschatten und Kernschatten bei einer totalen SoFi
Abb. 1: Halbschatten und Kernschatten bei einer totalen SoFi
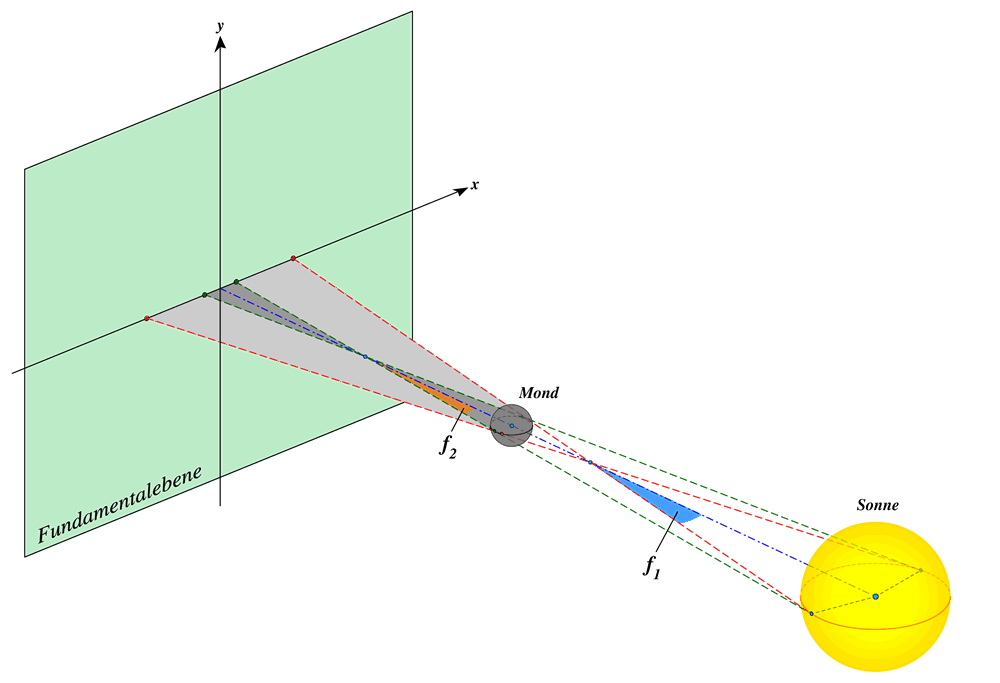 Abb. 2: Halbschatten und Kernschatten bei einer ringförmigen SoFi
Abb. 2: Halbschatten und Kernschatten bei einer ringförmigen SoFi
 Abb. 3: Halbschatten und Kernschatten bei einer Mondfinsternis
Abb. 3: Halbschatten und Kernschatten bei einer Mondfinsternis
Alle drei Grafiken sind nicht masstabsgetreu.
Die Finsternisgröße
$G$ bezeichnet die Finsternisgröße. $G = 0$ bei Beginn der partiellen Phase, $0 \lt G \lt 1$ beim Durchlaufen dieser Phase, $G = 1$ beim Beginn der Totalität, und $G \gt 1$ während der Totalität. Ist jedoch $G < 0$, so findet keine Finsternis statt.
Sonnenfinsternis
Die Größe $G$ der Finsternis wird nun ermittelt. Meeus schlägt folgende Gleichung vor: $$G = \frac{1,5433 + u - |\gamma|}{0,5461 + 2 \ u}\tag{52}$$
Bei einer partiellen Sonnenfinsternis wird die maximale Größe an dem Ort erreicht, der der Schattenachse am nächsten liegt. Eine erste Näherung der Sonnenfinsternisgröße ist (Handbuch für Sternfreunde): $$G = \frac{|\sigma| - \gamma + R_M}{2 \ R_M}\tag{53}$$
Die alternative Größe $G$ der Sonnenfinsternis (Montenbruck & Pfleger) ergibt sich mit den Schattenkegelradien $L_1$ und $L_2$ aus dem vorigen Abschnitt zu:
$$\text{totale Phase: } G = \frac{L_1 - L_2}{L_1 + L_2}\tag{54}$$ $$\text{partielle Phase: } G = \frac{L_1 - \gamma}{L_1 + L_2}\tag{55}$$
Mondfinsternis
Die Mondfinsternisgröße $G$ ist laut Handbuch für Sternfreunde: $$G = \frac{\sigma - \rho + R_M}{2 \ R_M}\tag{56}$$
Meeus bietet folgende Gleichungen an:
$$\text{Halbschattenfinsternis: } G = \frac{1,5573 + u - |\gamma|}{0,5450}\tag{57}$$ $$\text{Kernschattenfinsternis: } G = \frac{1,0128 - u - |\gamma|}{0,5450}\tag{58}$$
Positionswinkel
Um den Positionswinkel der Ein- und Austrittsrichtung des Mondes vor der Sonnenscheibe (Sonnenfinsternis) oder in und aus dem Erdschatten (Mondfinsternis) zu bestimmen, müssen die Mondkoordinaten $\alpha_M$, $\delta_M$ ins Fundamentalsystem transformiert werden (Montenbruck & Pfleger, Explanatory Supplement):
\[\begin{align} \cos(d_M) \cdot \cos(a_M) = &\; x_M = + \cos(\delta_M) \cdot \sin(\alpha_M - a) \\ \cos(d_M) \cdot \sin(a_M) = &\; y_M = - \cos(\delta_M) \cdot \cos(\alpha_M - a) \cdot \sin(d) + \sin(\delta_M) \cdot \cos(d) \\ \sin(d_M) = &\; z_M = + \cos(\delta_M) \cdot \cos(\alpha_M - a) \cdot \cos(d) + \sin(\delta_M) \cdot \sin(d) \end{align}\tag{59}\]
Ebenso muss die geografische Position $\lambda_0$, $\beta_0'$, samt Zählrichtung des Beobachters $\vec{e}_G$($\lambda_0$, $\beta_0'$) berücksichtigt und ins Fundamentalsystem transformiert werden
\[\begin{align} \cos(d_G) \cdot \cos(a_G) = &\; \xi = + \cos(\beta_0') \cdot \sin(\tau_0) \\ \cos(d_G) \cdot \sin(a_G) = &\; \eta = - \cos(\beta_0') \cdot \cos(\tau_0) \cdot \sin(d) + \sin(\beta_0') \cdot \cos(d) \\ \sin(d_G) = &\; \zeta = + \cos(\beta_0') \cdot \cos(\tau_0) \cos(d) + \sin(\beta_0') \cdot \sin(d) \end{align})\tag{60}\]
mit $\theta$ als der Sternzeit und $\tau_0$ = $\theta - \alpha\pm\lambda_0$ dem Stundenwinkel. $\pm$ gibt die alte/neue Zählrichtung der geografischen Länge an. Die Positionswinkel, die die Ein- und Austrittsrichtung des Mondes an der Sonnenscheibe für die partielle Phase ($L = L_1$) und die totale Phase ($L = L_2$) angibt, haben die Form: $$\begin{align} \cos(P) & = \frac{1}{L}\cdot (y_M - \eta) \\ \sin(P) & = \frac{1}{L}\cdot (x_M - \xi) \end{align}\tag{61}$$ Die Zählrichtung ist von Norden nach Osten im Uhrzeigersinn. Muss der Beobachtungsort wie bei einer Mondfinsternis nicht berücksichtigt werden, so reduziert sich obiger Vektor zu: $$\begin{align} \cos(P) &= y_M \\ \sin(P) &= x_M \end{align}\tag{62}$$
Die Koordinaten des solaren Gegenpunkts ($a, d$) sind $a = \textrm{red}\big(\alpha_S + 12^h, 24^h\big)$ und $d = -\delta_S$ mit der Reduktionsfunktion.
Sternbedeckungen
Dieser Beitrag hat ein eigenes Kapitel erhalten.
Legende
$D = l - L$ = das Argument der Länge des Mondes
$F = l - \Omega$ = das Argument der Breite des Mondes
$JDE_{SF/MF}$ = julianischer Tag für eine Sonnenfinsternis/Mondfinsternis
$T(JDE_{SF/MF})$, $T_1$, $T_2$ = vorläufige Finternistermine
$\vec{r}_S$ = $\vec{r}(\alpha_S, \delta_S, \Delta_S)$ = geozentrisch-äquatoriale Koordinaten der Sonne
$\vec{r}_M$ = $\vec{r}(\alpha_M, \delta_M, \Delta_M)$ = geozentrisch-äquatoriale Koordinaten des Mondes
$\vec{r}$ = $\vec{r}(a, d, g)$ = geozentrisch-äquatoriale Koordinaten des Schattenpunkts auf der Erdoberfläche
$\vec{r}_B$ = $\vec{r}(\alpha_B, \delta_B, R_E)$ = geozentrisch-äquatoriale Koordinaten des Beobachters auf der Erdoberfläche
$\vec{e}_G(\lambda_0, \beta_0', R_E)$ = geograf. Position des Beobachters im Fundamentalsystem
$\vec{e}_{MF}(a_M, d_M)$ = geozentrische Mondkoordinaten im Fundamentalsystem
$\vec{e}_{SF}(a_M, d_M)$ = geozentrische Sonnenkoordinaten im Fundamentalsystem
$\alpha_*$, $\delta_*$ = geozentrisch-äquatoriale Sternkoordinaten
$\alpha_P$, $\delta_P$ = geozentrisch-äquatoriale Planetenkoordinaten
$\Delta_M$ = modifizierter Mondabstand
$r_M$ = Mondabstand von der Erde
$r_{SM}$ = Mondabstand von der Sonne
$r_{SE}$ = Erdabstand R von der Sonne
$R_S$, $R_M$, $R_E$ = Radien der Sonne, des Mondes und der Erde
$d_M$ = Durchmesser des Kernschattens bei einer Mondfinsternis
$D_M$ = Durchmesser des Halbschattens bei einer Mondfinsternis
$d_S$ = Durchmesser des Kernschattens bei einer Sonnenfinsternis
$D_S$ = Durchmesser des Halbschattens bei einer Sonnenfinsternis
$\gamma$ = Abstand der Schattenachse vom Erdmittelpunkt
$\sigma$ = Mondelongation von der Sonne oder von dem solaren Gegenpunkt
$s$ = Abstand der Mondmitte zum Schattenpunkt auf der Erdoberfläche
$s_0$ = Entfernung des Mondmittelpunkts von der Fundamentalebene
$\rho$ = geringster Mondabstand vom Schattenpunkt auf der Erdoberfläche
$\tau$ = Finsternisdauer/Kontaktdauer bei Sternbedeckungen
$t$ = Zeitpunkt der Finsternismitte
$u$ = Radius des Kernschattenkegels des Mondes auf der Erde
$P$ = Positionswinkel des Finsternisein- und -austritts
$g$ = Abstand des Beobachters vom Mond in Bezug auf die Fundamentalebene
$L_1$ = Radius des Halbschattenkegels auf der Fundamentalebene
$L_2$ = Radius des Kernschattenkegels auf der Fundamentalebene
$\sqrt{\Delta}$ = Abstand der verfinsterten Erdoberfläche von der Fundamentalebene
$G$ = Finsternisgröße
$P, Q, A'$ = Hilfswerte