Dies ist eine alte Version des Dokuments!
Geozentrische Breite
Zur Bestimmung der topozentrischen Koordinaten (griech. $\tau\omicron\pi\omicron\varsigma$ Topos, Ort) eines Himmelkörpers benötigt man die geozentrischen Größen $\beta_0'$ und $\rho$. Dies ist meist nur für erdnahe Objekte wie z.B. den Mond notwendig, da der Mond eine relativ große Horizontalparallaxe von ca. $57''$ hat.
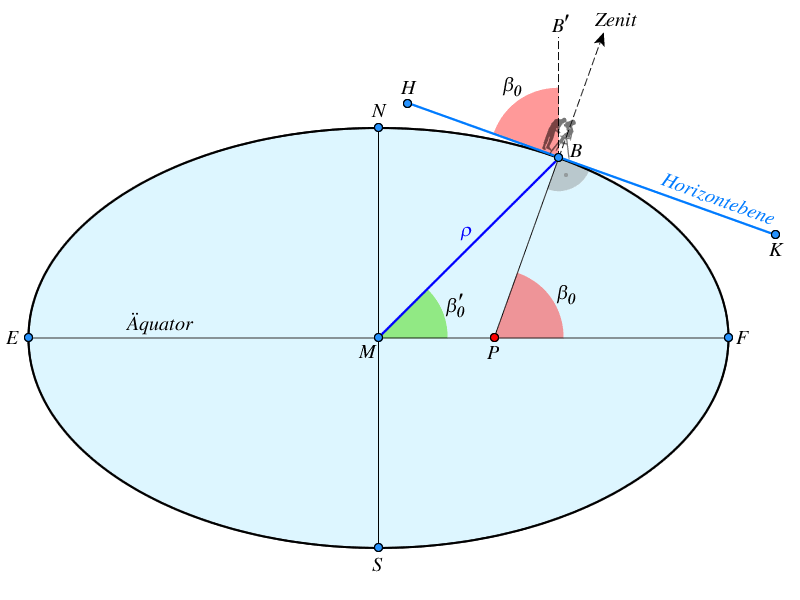
Winkel $\beta_0 = \angle FPB$ = geografische Breite des Beobachters in Grad
Winkel $\beta_0' =\angle FMB$ = geozentrische Breite des Beobachters in Grad
Abstand $\rho = \overline{MB}$ = geozentrischer Abstand des Beobachters vom Erdmittelpunkt in $km$
$R_E$ = Äquatorradius der Erde, $R_E = 6378.14\;km$, siehe Wichtige Konstanten
Abb.1 zeigt einen Meridianschnitt durch die Erde. Die Abplattung des Erdkörpers ist zu Anschauungszwecken extrem übertrieben dargestellt. $M$ ist der Erdmittelpunkt, $N$ und $S$ der Nord- bzw. Südpol. Die Verbindung $\overline{EF}$ stellt den Äquator dar, und $\overline{HK}$ ist die Horizontebene eines Beobachters $B$ auf der Erdoberfläche. Die Senkrechte zur Horizontebene in $B$ schneidet den Äquator im Punkt $P$.
Die Verbindung $\overline{BB'}$ ist parallel zur Richtung $\overline{NS}$, und die geografische Breite $\beta_0$ taucht als Winkel $\beta_0 = \angle B'BH$ wiederum auf.
Berechnung von $\beta_0'$ und $\rho$
Zur Umrechnung von geozentrischen äquatorialen Koordinaten in die topozentrischen äquatorialen Koordinaten müssen $\beta_0'$ und $\rho$ berechnet werden. Dies kann man mit folgenden Näherungsformeln erreichen: (Siehe ⇒ O.Montenbruck, Grundlagen der Ephemeridenrechnung)
\[ \begin{align} \beta_0' &\approx \beta_0- 0\overset{\circ}{.}1924\cdot \sin(2\beta_0) \\ \rho &\approx R_E - 21.38\cdot \sin^2(\beta_0) \end{align} \]
Am Äquator und am Pol ist die Abweichung der geozentrischen Breite $\beta_0'$ von der geografischen Breite $\beta_0$ gleich $0$. Die größte Abweichung erhält man für $\beta_0 = 45^\circ$ mit etwa $0\overset{\circ}{.}192425 = 0^\circ 11' 32\overset{''}{.}7$.
Nach Jean Meeus kann man die Größen $\beta_0'$ und $\rho$ auch wie folgt ermitteln. Zu beachten sind die Korrekturterme in Bogensekunden.
$$ \beta_0' \approx \beta_0 - 692\overset{''}{.}73\cdot \sin(2\beta_0) - 1\overset{''}{.}6\cdot \sin(4\beta_0) $$
und $\rho$ in Einheiten des Äquatorradius $R_E$
\[ \begin{align} \rho \approx\big{[}( & 0.9983271 \\ +&0.0016764\cdot \cos(2\beta_0) \\ -&0.0000035\cdot \cos(4\beta_0)\big{]}\cdot\ R_E \end{align} \]
Der geozentrische Abstand $\rho$ bezieht sich auf Meereshöhe, topografische Unebenheiten werden hier vernachlässigt.
In der Literatur wird die geographische Breite häufig mit $\varphi$ gekennzeichnet.