Dies ist eine alte Version des Dokuments!

−Inhaltsverzeichnis

Physische Ephemeriden

Physische Ephemeriden

Durchmesser

Es wird als erstes der scheinbare Durchmesser des Planetenscheibchens am Himmel berechnet, wie man diese durch ein Teleskop erkennen kann.

Tabelle 1
Objekt	Radius $\rho\,[km]$
$\odot$ Sonne:	696000.0
Merkur:	2439.7
Venus:	6051.9
Erde:	6378.14
Mars:	3396.2
Jupiter:	71492.0
Saturn:	60268.0
Uranus:	25559.0
Neptun:	24764.0

Ringe des Saturn: 136600.0 km

Daraus berechnet man mit Hilfe des Abstands $\Delta$ und des Planetenradius $\rho$ den scheinbaren Durchmesser $\varnothing$ :

$\varnothing = 2\cdot 3600''\cdot \arctan\left(\frac{\rho}{\Delta}\right)\tag{1}$

Dabei ist $\Delta$ in astronomischen Einheiten $AE$ zu setzen.

Phase & Beleuchtungsdefekt

Die Phase $k$ gibt den prozentual beleuchteten Anteil des Himmelsobjekts wieder. Der Beleuchtungsdefekt $d$ gibt den unbeleuchteten Anteil in Bogensekunden ( $''$ ) an.

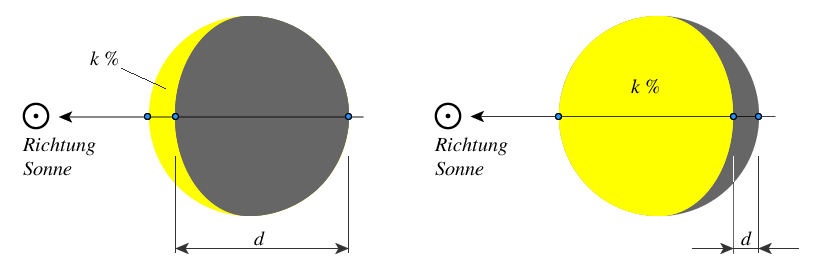Abb. 1: Phase, Beleuchtungsdefekt

Als erstes benötigt man den Phasenwinkel $\varphi$ :

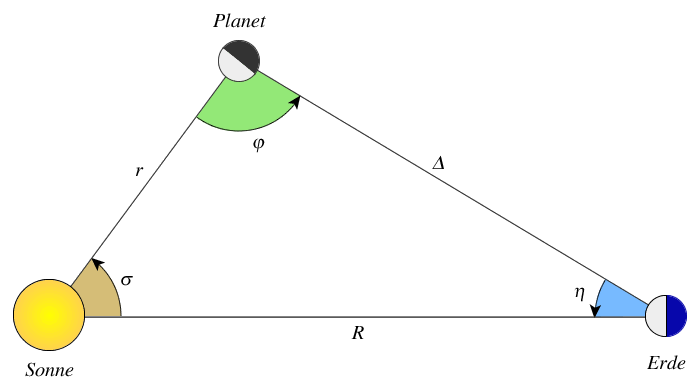Abb. 2: Phasenwinkel und Elongation

$\begin{align} \cos(\sigma) &= - \cos(L_S - l) \cdot \cos(b)\\ \cos (\eta) &= \cos(L_S - \lambda) \cdot \cos(\beta)\\ \varphi &= 180^{\circ} - (\sigma + \eta) \end{align}\tag{2}$

$l, b$ = heliozentrische Koordinaten des Objekts
$\lambda, \beta$ = geozentrische Koordinaten des Objekts
$L_S$ = geozentrische Länge der Sonne

Weiter gilt für den Phasenwinkel

$\cos(\varphi) = \frac{\Delta^2 + r^2 - R^2}{2\cdot \Delta \cdot r}\tag{3}$

$r\dots$ Entfernung des Planeten zur Sonne
$\Delta\dots$ Entfernung des Planeten zur Erde
$R\dots$ Entfernung der Erde zur Sonne
alle in astronomischen Einheiten $AU$ .

Die Phase $k$ und der Beleuchtungsdefekt $d$ sind dann gegeben durch:

$k = \frac{1}{2} \cdot (1 + \cos(\varphi)) \cdot 100\%\tag{4}$

$d = \frac{\varnothing}{2}\cdot (1 - \cos(\varphi))\tag{5}$

In der Literatur wird der Phasenwinkel manchmal mit der Variable $i$ gekennzeichnet.

Schiefe der Ekliptik zum Horizont

Die Schiefe der Ekliptik ist für Beobachtungen (insbesondere für Merkur, Venus und das Zodiakallicht) am Ost- oder Westhimmel wichtig, denn sie variiert im Laufe eines Sterntages und auch über das gesamte Jahr.

Abb. 3: Ekliptikschiefe zum Horizont

Die Transformationsmatrix lautet (J. Meeus): $\left( \begin{aligned} & \cos(90^{\circ} - \beta_e) \cdot \cos(90^{\circ} + \lambda_e) \\ & \cos(90^{\circ} - \beta_e) \cdot \sin(90^{\circ} + \lambda_e) \\ & \sin(90^{\circ} - \beta_e) \end{aligned} \right) = \left( \begin{aligned} & + \cos(\Theta) \cdot \cos(\beta_0) \\ & + \sin(\Theta) \cdot \cos(\beta_0) \cdot \cos(\varepsilon) + \sin(\beta_0) \cdot \sin(\varepsilon) \\ & - \sin(\Theta) \cdot \cos(\beta_0) \cdot \sin(\varepsilon) + \sin(\beta_0) \cdot \cos(\varepsilon) \end{aligned} \right)\tag{6}$

mit $\vec{e}$ ( $\Theta$ , $\beta_0$ ) als geozentrisch - äquatoriale Koordinaten des Zenits. Der Azimut der Horizontpunkte $A_e$ der Ekliptik ist dann laut G.D. Roth:

$A_e = \arcsin\left(- \frac{\sin(\lambda_e) \cdot \sin(\varepsilon)}{\cos(\beta_0)}\right)\tag{7}$

$90^{\circ} + \lambda_e$ ist der Winkel vom Frühlingspunkt entlang der Ekliptik zum lokalen Mittagsmerdian, während $90^{\circ} - \beta_e$ den Winkel zwischen dem Schnittpunkt Ekliptik/Mittagsmeridian und dem Zenit (entlang des Meridians) bildet. Kurz: Es handelt sich um die geozentrisch - ekliptikalen Koordinaten des Zenits.
$\beta_e$ ist nicht der Winkel, den die tägliche Sonnenbahn mit dem Horizont bildet. Die tägliche Bahn der Sonne am Taghimmel hat die gleiche Neigung zum Horizont wie der Himmelsäquator.

$\beta_e$ = Winkel zwischen Ekliptik und Horizont
$\varepsilon$ = Schiefe der Ekliptik
$\lambda_e$ = ekliptikale Länge der Horizontpunkte
$\beta_0$ = geographische Breite des Beobachtungsortes
$A_e$ = Azimut der Horizontpunkte
$\Theta$ = mittlere Ortssternzeit in Grad (Schnittpunkte zwischen Horizont und Ekliptik)

Elongation

Die Elongation $\eta$ kennzeichnet den Abstand des Himmelsobjekts von der Sonne. Die Formel wurde in der Phasenberechnung schon vorausgegriffen:

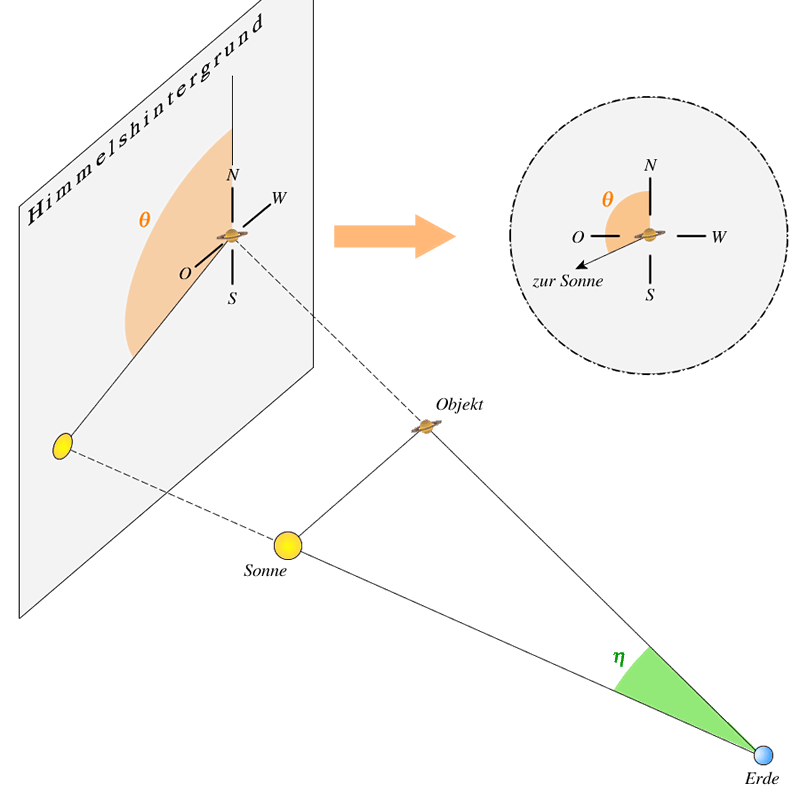Abb. 4: Elongation und Sonnenpositionswinkel

$\eta$ = Elongation = Winkel Objekt–Erde–Sonne (geozentrisch)
$\theta$ = Sonnenpositionswinkel = Winkel von der Nordrichtung nach Ost bis zur Verbindungslinie zur Sonne

$\cos(\eta) = \cos(L_S - \lambda)\cdot \cos(\beta)\tag{8}$

Sonnenpositionswinkel

Der Sonnenpositionswinkel $\theta$ gibt die Richtung an, aus der der Planet beleuchtet wird. Die Auflösung der karthesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Bei der Transformation muss diesmal darauf geachtet werden, dass die erhaltenen Werte noch nachträglich von 90 $^{\circ}$ abgezogen werden.

$\begin{align} \cos(90^{\circ} - \eta) \cdot \cos(90^{\circ} - \theta) =&\, x = \cos(B_S) \cdot \sin(L_S - \lambda) \\ \cos(90^{\circ} - \eta) \cdot \sin(90^{\circ} - \theta) =&\, y = -\cos(B_S) \cdot \cos(L_S - \lambda) \cdot \sin(\beta) + \sin(B_S) \cdot \cos(\beta) \\ \sin(90^{\circ} - \eta) =&\, z = \cos(B_S) \cdot \cos(L_S - \lambda) \cdot \cos(\beta) + \sin(B_S) \cdot \sin(\beta)\end{align}\tag{9}$

$L_S$ , $B_S$ = geozentrisch ekliptikale Koordinaten der Sonne
Dabei ist $\eta$ wieder die Elongation.

Parallaktischer Winkel

Der parallaktische Winkel $q$ ist die Neigung der beleuchteten Planeten- oder Mondscheibe relativ zum Horizont und $z$ ist die Zenitdistanz.

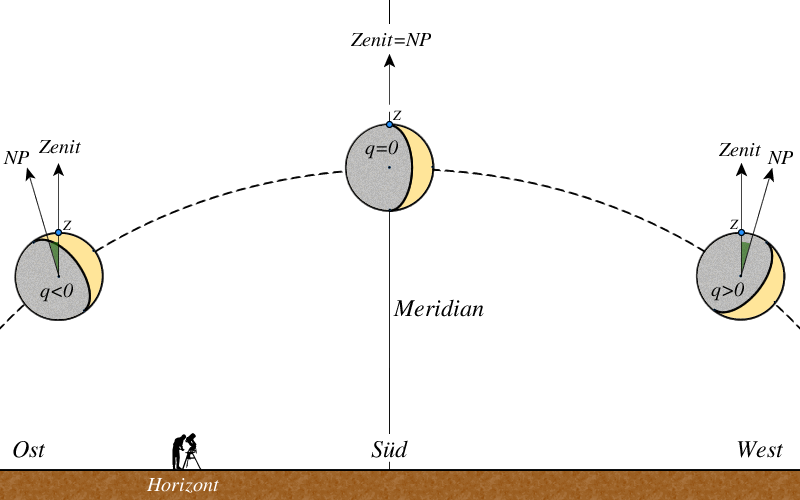Abb. 5: Die Neigung der Sichel zum Horizont

Hat man die geozentrisch äquatorialen Koordinaten $\alpha$ , $\delta$ des Planeten oder Mondes, die geographische Breite $\beta_0$ des Beobachters und die lokale Sternzeit $\theta$ , so kann man mit dem folgenden Ausdruck den parallaktischen Winkel $q$ berechnen:

$\begin{align} \cos(90^{\circ} - z) \cdot \cos(90^{\circ} - q) &= x = + \cos(\beta_0) \cdot \sin(\theta - \alpha) \\ \cos(90^{\circ} - z) \cdot \sin(90^{\circ} - q) &= y = - \cos(\beta_0) \cdot \cos(\theta - \alpha) \cdot \sin(\delta) + \sin(\beta_0) \cdot \cos(\delta) \\ \sin(90^{\circ} - z) &= z = + \cos(\beta_0) \cdot \cos(\theta - \alpha) \cdot \cos(\delta) + \sin(\beta_0) \cdot \sin(\delta) \end{align}\tag{10}$

Bei Auf- und Untergängen reduziert sich $q$ auf die Gleichung: $\cos(q) = \frac{\sin(\beta_0)}{\cos(\delta)}\tag{11}$

Der parallaktische Winkel $q$ wird vom Zenit aus im Uhrzeigersinn gezählt. $q$ ist negativ vor der Kulmination und positiv nach der Kulmination. Im Zenit selbst ist $q$ jedoch nicht definiert.

Morgen- und Abendweite

Den Auf- und Untergangspunkt $A$ am Horizont findet man mit: $\cos(A) = -\frac{\sin(\delta)}{\cos(\beta_0)}\tag{12}$

$A$ wird auch als die Morgenweite beim Aufgang oder als Abendweite beim Untergang bezeichnet, unabhängig davon wann der Auf- und Untergang stattfindet.

Helligkeit

Die nachfolgenden Gleichungen beschreiben die absolute Helligkeit $m_0$ der Planeten in $1 AE$ Abstand. Wichtig ist hier auch der Phasenwinkel $\varphi$ .

Tabelle 2
Planet	Absolute Helligkeit
Merkur	$\begin{align} m_0 = &-0\overset{m}{.}42 \\ &+3\overset{m}{.}8 \left(\frac{\varphi}{100^{\circ}} \right) \\ &-2\overset{m}{.}73 \left(\frac{\varphi}{100^{\circ}} \right)^2 \\ &+2\overset{m}{.}00 \left(\frac{\varphi}{100^{\circ}} \right)^3\end{align}$
Venus	$\begin{align} m_0 = &-4\overset{m}{.}40 \\ &+0\overset{m}{.}009 \left(\frac{\varphi}{100^{\circ}} \right) \\ &+2\overset{m}{.}39 \left(\frac{\varphi}{100^{\circ}} \right)^2 \\ &-0\overset{m}{.}65 \left(\frac{\varphi}{100^{\circ}} \right)^3\end{align}$
Erde	$\begin{align} m_0 = &-3\overset{m}{.}87 \\ &+1\overset{m}{.}30 \left(\frac{\eta}{100^{\circ}} \right) \\ &+0\overset{m}{.}19 \left(\frac{\eta}{100^{\circ}} \right)^2 \\ &+0\overset{m}{.}48 \left(\frac{\eta}{100^{\circ}} \right)^3\end{align}$
Mars	$\begin{align} m_0 = &-1\overset{m}{.}52 \\ &+1\overset{m}{.}60 \left(\frac{\varphi}{100^{\circ}} \right)\end{align}$
Jupiter	$\begin{align} m_0 = &-9\overset{m}{.}40 \\ &+0\overset{m}{.}50 \left(\frac{\varphi}{100^{\circ}} \right)\end{align}$
Saturn*	$\begin{align} m_0 = &-8\overset{m}{.}88 \\ &+4\overset{m}{.}40 \left(\frac{\varphi}{100^{\circ}} \right) \\ &-2\overset{m}{.}60 \cdot\sin (\|\color{#ff00ff}{D_E}\|) \\ &+1\overset{m}{.}25 \cdot\sin (\|\color{#ff00ff}{D_E}\|)^2\end{align}$
Uranus	$\begin{align} m_0 = &-7\overset{m}{.}19 \\ &+0\overset{m}{.}28 \left(\frac{\varphi}{100^{\circ}} \right)\end{align}$
Neptun	$\begin{align} m_0 = &-7\overset{m}{.}05 \\ &+0\overset{m}{.}54 \left(\frac{\varphi}{100^{\circ}} \right)\end{align}$

Die scheinbare Helligkeit $m$ aus $\Delta AE$ Entfernung berechnet man mit der folgenden Gleichung:

$m = m_0 + 5\cdot \log_{10}\left(\frac{r\cdot \Delta}{1 AE^2}\right)\tag{13}$

Die Helligkeit ist dem Explanatory Supplement entnommen worden. Die scheinbare Helligkeit der Erde stammt aus D.L. Harris (Photometry and Colormetry of Planets and Satellites), die Phasenterme für Uranus und Neptun haben ihren Ursprung in dem Paper von G.W. Lockwood, D.T. Thomson et al..

* $\color{#ff00ff}{D_E}$ ist die planetozentrische Breite der Erde über der Äquatorebene des Saturn (Ringneigung). Dies und die zugehörigen Rotationselemente werden im nachfolgenden Abschnitt beschrieben. Für die Erde ist $\eta$ ihre planetozentrische Elongation zur Sonne.
Die hier präsentierten Helligkeiten der Planeten haben nur einen begrenzten Gültigkeitszeitraum. In einem eigenen Beitrag wird die Situation näher illustriert.

Rotation

Zur Berechnung der Rotationen der Sonne und der Planeten benötigt man vorab die Rotationselemente. $T$ bezieht sich auf die Epoche J2000.0. Siehe auch den Abschnitt über den Julianischer Tag JD.

Tabelle 3
Planet	$\alpha_0$		$\Delta\alpha$	$\delta_0$		$\Delta\delta$
Sonne:	$+286\overset{\circ}{.}13$		$+0\overset{\circ}{.}183\cdot T$	$+63\overset{\circ}{.}87$		$+0\overset{\circ}{.}154\cdot T$
Merkur:	$+281\overset{\circ}{.}01$	$-0\overset{\circ}{.}033\cdot T$	$+0\overset{\circ}{.}276\cdot T$	$+61\overset{\circ}{.}45$	$-0\overset{\circ}{.}005\cdot T$	$+0\overset{\circ}{.}107\cdot T$
Venus:	$+272\overset{\circ}{.}76$		$-0\overset{\circ}{.}043\cdot T$	$+67\overset{\circ}{.}16$		$+0\overset{\circ}{.}027\cdot T$
Erde:	$+0\overset{\circ}{.}00$	$-0\overset{\circ}{.}641\cdot T$	$+0\overset{\circ}{.}640\cdot T$	$+90\overset{\circ}{.}00$	$-0\overset{\circ}{.}557\cdot T$	$+0\overset{\circ}{.}557\cdot T$
Mars:	$+317\overset{\circ}{.}68143$	$-0\overset{\circ}{.}1061\cdot T$	$+0\overset{\circ}{.}786\cdot T$	$+52\overset{\circ}{.}8865$	$0\overset{\circ}{.}0609\cdot T$	$+0\overset{\circ}{.}413\cdot T$
Jupiter:	$+268\overset{\circ}{.}05$	$-0\overset{\circ}{.}009\cdot T$	$+0\overset{\circ}{.}116\cdot T$	$+64\overset{\circ}{.}49$	$+0\overset{\circ}{.}003\cdot T$	$-0\overset{\circ}{.}018\cdot T$
Saturn:	$+40\overset{\circ}{.}589$	$-0\overset{\circ}{.}036\cdot T$	$+4\overset{\circ}{.}731\cdot T$	$+83\overset{\circ}{.}537$	$-0\overset{\circ}{.}004\cdot T$	$+0\overset{\circ}{.}407\cdot T$
Uranus:	$+257\overset{\circ}{.}311$		$+1\overset{\circ}{.}429\cdot T$	$-15\overset{\circ}{.}175$		$-0\overset{\circ}{.}114\cdot T$
Neptun:	$+299\overset{\circ}{.}36$	$+0\overset{\circ}{.}70\cdot\sin (\color{#ff00ff}{N})$	$+0\overset{\circ}{.}849\cdot T$	$+43\overset{\circ}{.}46$	$-0\overset{\circ}{.}51\cdot\cos (\color{#ff00ff}{N})$	$+0\overset{\circ}{.}242\cdot T$

mit $\color{#ff00ff}N = 357\overset{\circ}{.}85 + 52\overset{\circ}{.}316\cdot T$ .

Die Rotationselemente $\alpha_0$ und $\delta_0$ bezeichnen die erdäquatoriale Lage der Rotationsachsen der Planeten. Es folgt die Tabelle mit den Nullmeridianen $W$ :

Tabelle 4
Planet	System	$W_0$	$\text{d}W$	$\Delta W$
Sonne:		$+84\overset{\circ}{.}182$	$+14\overset{\circ}{.}1844$	$+1\overset{\circ}{.}222$
Merkur:		$+329\overset{\circ}{.}68$	$+6\overset{\circ}{.}1385025$	$+1\overset{\circ}{.}145$
Venus:		$+160\overset{\circ}{.}20$	$-1\overset{\circ}{.}4813688$	$+1\overset{\circ}{.}436$
Erde:		$+190\overset{\circ}{.}147$	$+360\overset{\circ}{.}9856235$	$+0\overset{\circ}{.}624$
Mars:		$+176\overset{\circ}{.}630$	$+350\overset{\circ}{.}89198226$	$+0\overset{\circ}{.}620$
Jupiter:	System I:	$+67\overset{\circ}{.}10$	$+877\overset{\circ}{.}9$	$+1\overset{\circ}{.}291$
	System II:	$+43\overset{\circ}{.}30$	$+870\overset{\circ}{.}27$	$+1\overset{\circ}{.}291$
	System III:	$+284\overset{\circ}{.}95$	$+870\overset{\circ}{.}5366420$	$+1\overset{\circ}{.}291$
Saturn:	System I:	$+227\overset{\circ}{.}2037$	$+844\overset{\circ}{.}3$	$+3\overset{\circ}{.}470$
	System II:	$+105\overset{\circ}{.}4857$	$+812\overset{\circ}{.}0$	$+3\overset{\circ}{.}470$
	System III:	$+38\overset{\circ}{.}90$	$+810\overset{\circ}{.}7939024$	$+3\overset{\circ}{.}470$
Uranus:		$+203\overset{\circ}{.}81$	$-501\overset{\circ}{.}1600928$	$+0\overset{\circ}{.}564$
Neptun:		$+253\overset{\circ}{.}18$	$+536\overset{\circ}{.}3128492$	$+0\overset{\circ}{.}662$

Der Nullmeridian ist ein willkürlicher, aber festgelegter Wert auf der Oberfläche des Planeten. Er berechnet sich mit

$W = W_0 + \textrm{d}W \cdot T + \Delta W\tag{14}$

Die hier präsentierten Rotationselemente haben nur einen begrenzten Gültigkeitszeitraum. In einem eigenen Beitrag wird die Situation näher illustriert.

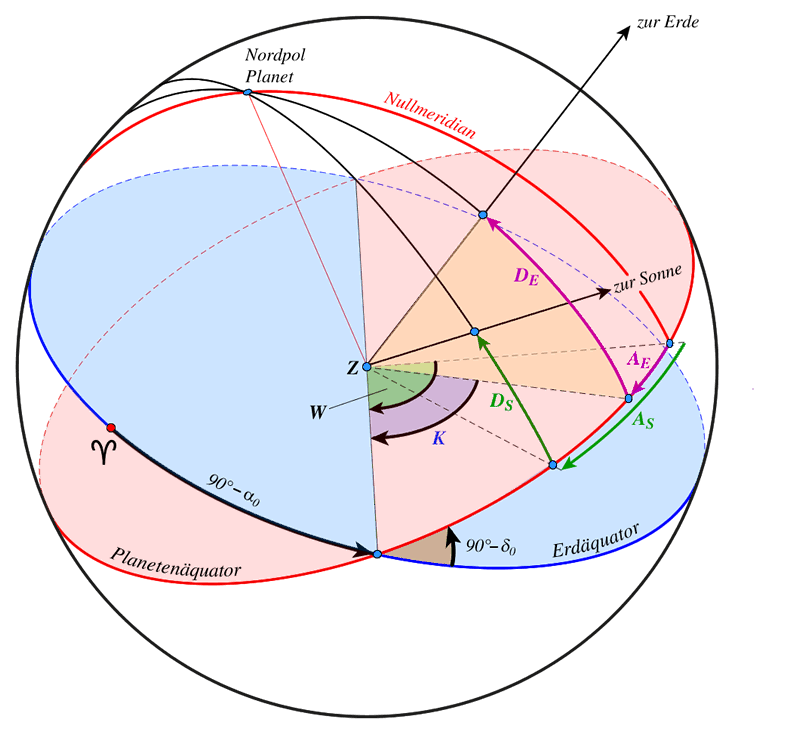Abb. 6: Größen zur Planetenrotation

$\begin{align} \cos(D_E) \cdot \cos(K) =&\, x = +\cos(\delta) \cdot \sin(\alpha_0 - \alpha) \\ \cos(D_E) \cdot \sin(K) =&\, y = +\cos(\delta) \cdot \cos(\alpha_0 - \alpha) \cdot \sin(\delta_0) - \sin(\delta) \cdot \cos(\delta_0) \\ \sin(D_E) =&\, z = -\cos(\delta) \cdot \cos(\alpha_0 - \alpha) \cdot \cos(\delta_0) - \sin(\delta) \cdot \sin(\delta_0) \end{align}\tag{15}$

$D_E$ ist die planetozentrische Breite der Erde über dem planetaren Äquator. Damit ergibt sich planetozentrische Länge der Erde $A_E$ vom Nullmeridian des Planeten. $A_E = (W - K)\cdot \text{sgn}\left(\frac{\textrm{d}W}{\textrm{d}T}\right)\tag{16}$

Die Signum-Funktion stammt aus dem Abschnitt über die Vorzeichenfunktion. Die Auflösung der karthesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Man erhält die planetozentrisch äquatorialen Koordinaten $A_E$ (Länge) und $D_E$ (Breite) der Erde vom Planeten aus gesehen. Abb. 7: Positionswinkel

$\begin{align} \cos(D_E) \cdot \cos(P) =&\, x = -\cos(\delta_0) \cdot \cos(\alpha_0 - \alpha) \cdot \sin(\delta) + \cos(\delta) \cdot \sin(\delta_0) \\ \cos(D_E) \cdot \sin(P) =&\, y = +\cos(\delta_0) \cdot \sin(\alpha_0 - \alpha) \\ \sin(D_E) =&\, z = -\cos(\delta) \cdot \cos(\alpha_0 - \alpha) \cdot \cos(\delta_0) - \sin(\delta) \cdot \sin(\delta_0) \end{align}\tag{17}$

$D_E$ ist wieder die planetozentrische Breite der Erde. Die Auflösung der karthesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Man erhält den Positionswinkel der planetaren Rotationsachse $P$ .

Die Rotationselemente (samt Nullmeridian) stammen aus dem Explanatory Supplement und aus dem Report der IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites. Der Nullmeridian System III für Jupiter und System II stammen von K.H. Bücke; siehe auch die Literaturhinweise.