Inhaltsverzeichnis
Physische Ephemeriden
Durchmesser
Es wird als erstes der scheinbare Durchmesser des Planetenscheibchens am Himmel berechnet, wie man dieses durch ein Teleskop erkennen kann.
| Tabelle 1 | |
|---|---|
| Objekt | Radius $\rho\,[km]$ |
| $\odot$ Sonne: | 696000.0 |
| | 2439.7 |
| | 6051.9 |
| | 6378.14 |
| | 3396.2 |
| | 71492.0 |
| | 60268.0 |
| | 25559.0 |
| | 24764.0 |
Ringe des Saturn: 136600.0 km
Daraus berechnet man mit Hilfe des Abstands $\Delta$ und des Planetenradius $\rho$ den scheinbaren Durchmesser $\varnothing$:
$$\varnothing = 2\cdot 3600''\cdot \arctan\left(\frac{\rho}{\Delta}\right)\tag{1}$$
Dabei ist $\Delta$ in astronomischen Einheiten $AE$ zu setzen.
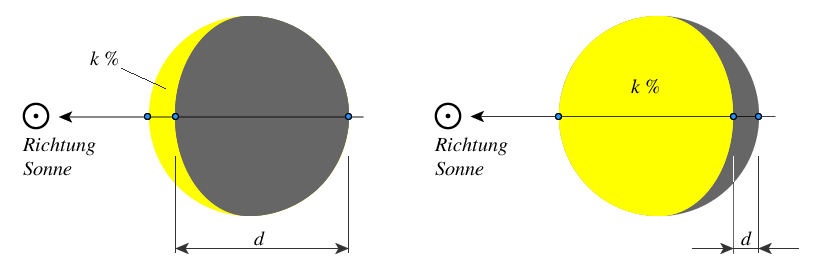
Phase & Beleuchtungsdefekt
Als nächstes wird die Phase des Planetenscheibchens berechnet. Die Phase $k$ gibt den prozentual beleuchteten Anteil des Himmelsobjekts wieder. Der Beleuchtungsdefekt $d$ gibt den unbeleuchteten Anteil in Bogensekunden ($''$) an.
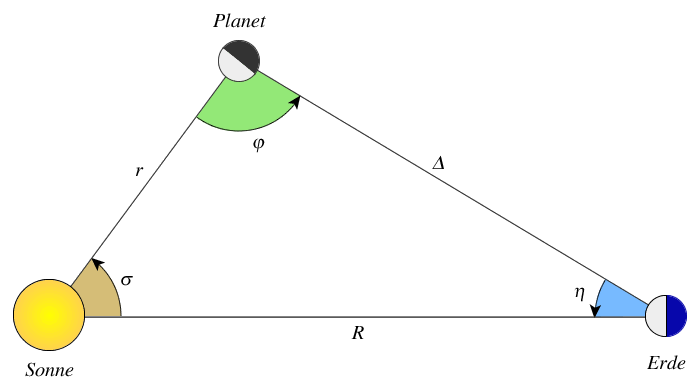
Als erstes benötigt man den Phasenwinkel $\varphi$:
\[\begin{align} \cos(\sigma) &= - \cos(L_S - l) \cdot \cos(b)\\ \cos (\eta) &= \cos(L_S - \lambda) \cdot \cos(\beta)\\ \varphi &= 180^{\circ} - (\sigma + \eta) \end{align}\tag{2}\]
$l, b$ = heliozentrische Koordinaten des Objekts
$\lambda, \beta$ = geozentrische Koordinaten des Objekts
$L_S$ = geozentrische Länge der Sonne
Weiter gilt für den Phasenwinkel
$$\cos(\varphi) = \frac{\Delta^2 + r^2 - R^2}{2\cdot \Delta \cdot r}\tag{3}$$
$r$ = Entfernung des Planeten zur Sonne
$\Delta$ = Entfernung des Planeten zur Erde
$R$ = Entfernung der Erde zur Sonne
Alle drei Parameter sind in astronomischen Einheiten $AU$ gehalten.
Die Phase $k$ und der Beleuchtungsdefekt $d$ sind dann gegeben durch:
$$k = \frac{1}{2} \cdot (1 + \cos(\varphi)) \cdot 100\%\tag{4}$$
$$d = \frac{\varnothing}{2}\cdot (1 - \cos(\varphi))\tag{5}$$
In der Literatur wird der Phasenwinkel manchmal mit der Variable $i$ gekennzeichnet.
Schiefe der Ekliptik zum Horizont
Die Schiefe der Ekliptik ist für Beobachtungen (insbesondere für Merkur, Venus und das Zodiakallicht) am Ost- oder Westhimmel wichtig, denn sie variiert im Laufe eines Sterntages und auch über das gesamte Jahr.
 Abb. 3: Ekliptikschiefe zum Horizont
Abb. 3: Ekliptikschiefe zum Horizont
Die Transformationsmatrix lautet (J. Meeus): \[\left( \begin{aligned} & \cos(90^{\circ} - \beta_e) \cdot \cos(90^{\circ} + \lambda_e) \\ & \cos(90^{\circ} - \beta_e) \cdot \sin(90^{\circ} + \lambda_e) \\ & \sin(90^{\circ} - \beta_e) \end{aligned} \right) = \left( \begin{aligned} & + \cos(\Theta) \cdot \cos(\beta_0) \\ & + \sin(\Theta) \cdot \cos(\beta_0) \cdot \cos(\varepsilon) + \sin(\beta_0) \cdot \sin(\varepsilon) \\ & - \sin(\Theta) \cdot \cos(\beta_0) \cdot \sin(\varepsilon) + \sin(\beta_0) \cdot \cos(\varepsilon) \end{aligned} \right)\tag{6}\]
mit $\vec{e}$($\Theta$, $\beta_0$) als geozentrisch-äquatoriale Koordinaten des Zenits. Der Azimut der Horizontpunkte $A_e$ der Ekliptik ist dann laut G.D. Roth:
$$A_e = \arcsin\left(-\frac{\sin(\lambda_e)\cdot\sin(\varepsilon)}{\cos(\beta_0)}\right)\tag{7}$$
- $90^{\circ} + \lambda_e$ ist der Winkel vom Frühlingspunkt entlang der Ekliptik zum lokalen Mittagsmeridian, während $90^{\circ} - \beta_e$ den Winkel zwischen dem Schnittpunkt Ekliptik/Mittagsmeridian und dem Zenit (entlang des Meridians) bildet. Kurz: Es handelt sich um die geozentrisch-ekliptikalen Koordinaten des Zenits.
- $\beta_e$ ist nicht der Winkel, den die tägliche Sonnenbahn mit dem Horizont bildet. Die tägliche Bahn der Sonne am Taghimmel hat die gleiche Neigung zum Horizont wie der Himmelsäquator.
$\beta_e$ = Winkel zwischen Ekliptik und Horizont
$\varepsilon$ = Schiefe der Ekliptik
$\lambda_e$ = ekliptikale Länge der Horizontpunkte
$\beta_0$ = geographische Breite des Beobachtungsortes
$A_e$ = Azimut der Horizontpunkte
$\Theta$ = mittlere Ortssternzeit in Grad (Schnittpunkte zwischen Horizont und Ekliptik)
Elongation
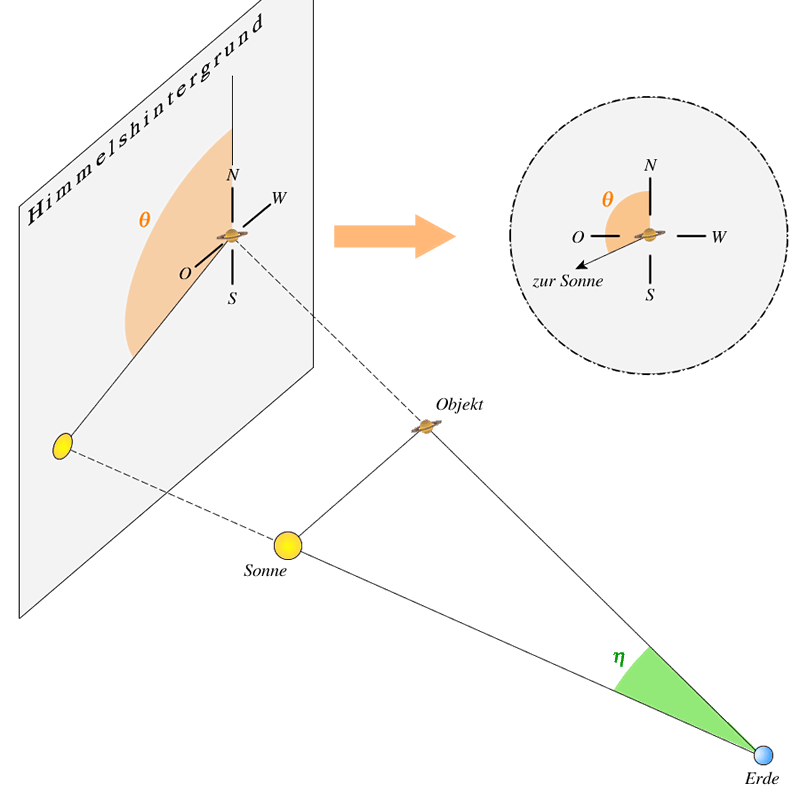
Die Elongation $\eta$ kennzeichnet den Abstand des Himmelsobjekts von der Sonne. Die Formel wurde in der Phasenberechnung schon vorausgegriffen:
$\eta$ = Elongation = Winkel Objekt–Erde–Sonne (geozentrisch)
$\theta$ = Sonnenpositionswinkel = Winkel von der Nordrichtung nach Ost bis zur Verbindungslinie zur Sonne
$$\cos(\eta) = \cos(L_S - \lambda)\cdot \cos(\beta)\tag{8}$$
Sonnenpositionswinkel
Der Sonnenpositionswinkel $\theta$ gibt die Richtung an, aus der der Planet beleuchtet wird. Die Auflösung der kartesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Bei der Transformation muss diesmal darauf geachtet werden, dass die erhaltenen Werte noch nachträglich von 90$^{\circ}$ abgezogen werden.
\[\begin{align} \cos(90^{\circ} - \eta) \cdot \cos(90^{\circ} - \theta) =&\, x = \cos(B_S) \cdot \sin(L_S - \lambda) \\ \cos(90^{\circ} - \eta) \cdot \sin(90^{\circ} - \theta) =&\, y = -\cos(B_S) \cdot \cos(L_S - \lambda) \cdot \sin(\beta) + \sin(B_S) \cdot \cos(\beta) \\ \sin(90^{\circ} - \eta) =&\, z = \cos(B_S) \cdot \cos(L_S - \lambda) \cdot \cos(\beta) + \sin(B_S) \cdot \sin(\beta)\end{align}\tag{9}\]
$L_S$, $B_S$ = geozentrisch ekliptikale Koordinaten der Sonne
Dabei ist $\eta$ wieder die Elongation.
Parallaktischer Winkel
Der parallaktische Winkel $q$ ist die Neigung der beleuchteten Planeten- oder Mondscheibe relativ zum Horizont und $z$ ist die Zenitdistanz.
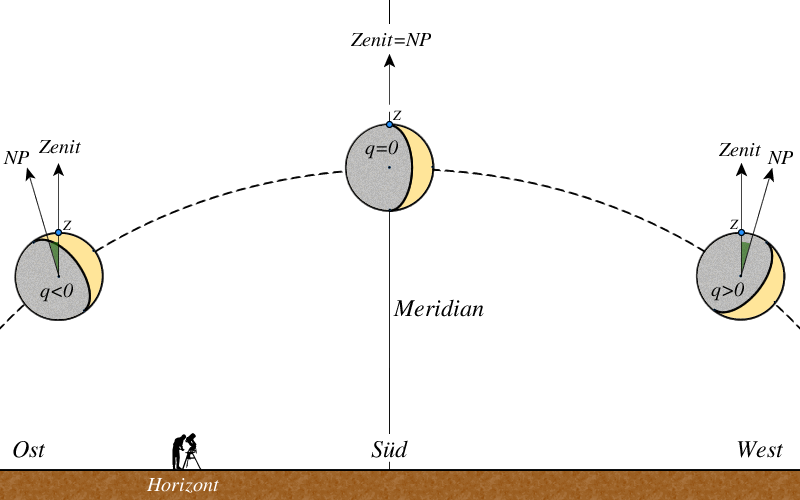 Abb. 5: Die Neigung der Sichel zum Horizont
Abb. 5: Die Neigung der Sichel zum Horizont
Hat man die geozentrisch äquatorialen Koordinaten $\alpha$, $\delta$ des Planeten oder Mondes, die geographische Breite $\beta_0$ des Beobachters und die lokale Sternzeit $\theta$, so kann man mit dem folgenden Ausdruck den parallaktischen Winkel $q$ berechnen:
\[\begin{align} \cos(90^{\circ} - z) \cdot \cos(90^{\circ} - q) &= x = + \cos(\beta_0) \cdot \sin(\theta - \alpha) \\ \cos(90^{\circ} - z) \cdot \sin(90^{\circ} - q) &= y = - \cos(\beta_0) \cdot \cos(\theta - \alpha) \cdot \sin(\delta) + \sin(\beta_0) \cdot \cos(\delta) \\ \sin(90^{\circ} - z) &= z = + \cos(\beta_0) \cdot \cos(\theta - \alpha) \cdot \cos(\delta) + \sin(\beta_0) \cdot \sin(\delta) \end{align}\tag{10}\]
Bei Auf- und Untergängen reduziert sich $q$ auf die Gleichung: $$\cos(q) = \frac{\sin(\beta_0)}{\cos(\delta)}\tag{11}$$
Der parallaktische Winkel $q$ wird vom Zenit aus im Uhrzeigersinn gezählt. $q$ ist negativ vor der Kulmination und positiv nach der Kulmination. Im Zenit selbst ist $q$ jedoch nicht definiert.
Morgen- und Abendweite
Den Auf- und Untergangspunkt $A$ am Horizont findet man mit: $$\cos(A) = -\frac{\sin(\delta)}{\cos(\beta_0)}\tag{12}$$
$A$ wird auch als die Morgenweite beim Aufgang oder als Abendweite beim Untergang bezeichnet, unabhängig davon wann der Auf- und Untergang stattfindet.
Helligkeit
Die nachfolgenden Gleichungen beschreiben die absolute Helligkeit $m_0$ der Planeten in $1 AE$ Abstand. Wichtig ist hier auch der Phasenwinkel $\varphi$.
| Tabelle 2 | |
|---|---|
| Planet | Absolute Helligkeit |
| Merkur | $\begin{align} m_0 = &-0\overset{m}{.}42 \\ &+3\overset{m}{.}8 \left(\frac{\varphi}{100^{\circ}} \right) \\ &-2\overset{m}{.}73 \left(\frac{\varphi}{100^{\circ}} \right)^2 \\ &+2\overset{m}{.}00 \left(\frac{\varphi}{100^{\circ}} \right)^3\end{align}$ |
| Venus | $\begin{align} m_0 = &-4\overset{m}{.}40 \\ &+0\overset{m}{.}009 \left(\frac{\varphi}{100^{\circ}} \right) \\ &+2\overset{m}{.}39 \left(\frac{\varphi}{100^{\circ}} \right)^2 \\ &-0\overset{m}{.}65 \left(\frac{\varphi}{100^{\circ}} \right)^3\end{align}$ |
| Erde | $\begin{align} m_0 = &-3\overset{m}{.}87 \\ &+1\overset{m}{.}30 \left(\frac{\eta}{100^{\circ}} \right) \\ &+0\overset{m}{.}19 \left(\frac{\eta}{100^{\circ}} \right)^2 \\ &+0\overset{m}{.}48 \left(\frac{\eta}{100^{\circ}} \right)^3\end{align}$ |
| Mars | $\begin{align} m_0 = &-1\overset{m}{.}52 \\ &+1\overset{m}{.}60 \left(\frac{\varphi}{100^{\circ}} \right)\end{align}$ |
| Jupiter | $\begin{align} m_0 = &-9\overset{m}{.}40 \\ &+0\overset{m}{.}50 \left(\frac{\varphi}{100^{\circ}} \right)\end{align}$ |
| Saturn* | $\begin{align} m_0 = &-8\overset{m}{.}88 \\ &+4\overset{m}{.}40 \left(\frac{\varphi}{100^{\circ}} \right) \\ &-2\overset{m}{.}60 \cdot\sin (|\color{#ff00ff}{D_E}|) \\ &+1\overset{m}{.}25 \cdot\sin (|\color{#ff00ff}{D_E}|)^2\end{align}$ |
| Uranus | $\begin{align} m_0 = &-7\overset{m}{.}19 \\ &+0\overset{m}{.}28 \left(\frac{\varphi}{100^{\circ}} \right)\end{align}$ |
| Neptun | $\begin{align} m_0 = &-7\overset{m}{.}05 \\ &+0\overset{m}{.}54 \left(\frac{\varphi}{100^{\circ}} \right)\end{align}$ |
Die scheinbare Helligkeit $m$ aus $\Delta AE$ Entfernung berechnet man mit der folgenden Gleichung:
$$m = m_0 + 5\cdot \log_{10}\left(\frac{r\cdot \Delta}{1 AE^2}\right)\tag{13}$$
Die Helligkeit ist dem Explanatory Supplement entnommen worden. Die scheinbare Helligkeit der Erde stammt aus D.L. Harris (Photometry and Colormetry of Planets and Satellites), die Phasenterme für Uranus und Neptun haben ihren Ursprung in dem Paper von G.W. Lockwood, D.T. Thomson et al..
- *$\color{#ff00ff}{D_E}$ ist die planetozentrische Breite der Erde über der Äquatorebene des Saturn (Ringneigung). Dies und die zugehörigen Rotationselemente werden im nachfolgenden Abschnitt beschrieben. Für die Erde ist $\eta$ ihre planetozentrische Elongation zur Sonne.
- Die hier präsentierten Helligkeiten der Planeten haben nur einen begrenzten Gültigkeitszeitraum. In einem eigenen Beitrag wird die Situation näher illustriert.
Rotation
Zur Berechnung der Rotationen der Sonne und der Planeten benötigt man vorab die Rotationselemente. $T$ bezieht sich auf die Epoche J2000.0. Siehe auch den Abschnitt über den Julianischer Tag JD.
| Tabelle 3 | ||||||
|---|---|---|---|---|---|---|
| Planet | $\alpha_0$ | $\Delta\alpha$ | $\delta_0$ | $\Delta\delta$ | ||
| Sonne: | $+286\overset{\circ}{.}13$ | $+0\overset{\circ}{.}183\cdot T$ | $+63\overset{\circ}{.}87$ | $+0\overset{\circ}{.}154\cdot T$ | ||
| Merkur: | $+281\overset{\circ}{.}01$ | $-0\overset{\circ}{.}033\cdot T$ | $+0\overset{\circ}{.}276\cdot T$ | $+61\overset{\circ}{.}45$ | $-0\overset{\circ}{.}005\cdot T$ | $+0\overset{\circ}{.}107\cdot T$ |
| Venus: | $+272\overset{\circ}{.}76$ | $-0\overset{\circ}{.}043\cdot T$ | $+67\overset{\circ}{.}16$ | $+0\overset{\circ}{.}027\cdot T$ | ||
| Erde: | $+0\overset{\circ}{.}00$ | $-0\overset{\circ}{.}641\cdot T$ | $+0\overset{\circ}{.}640\cdot T$ | $+90\overset{\circ}{.}00$ | $-0\overset{\circ}{.}557\cdot T$ | $+0\overset{\circ}{.}557\cdot T$ |
| Mars: | $+317\overset{\circ}{.}68143$ | $-0\overset{\circ}{.}1061\cdot T$ | $+0\overset{\circ}{.}786\cdot T$ | $+52\overset{\circ}{.}8865$ | $0\overset{\circ}{.}0609\cdot T$ | $+0\overset{\circ}{.}413\cdot T$ |
| Jupiter: | $+268\overset{\circ}{.}05$ | $-0\overset{\circ}{.}009\cdot T$ | $+0\overset{\circ}{.}116\cdot T$ | $+64\overset{\circ}{.}49$ | $+0\overset{\circ}{.}003\cdot T$ | $-0\overset{\circ}{.}018\cdot T$ |
| Saturn: | $+40\overset{\circ}{.}589$ | $-0\overset{\circ}{.}036\cdot T$ | $+4\overset{\circ}{.}731\cdot T$ | $+83\overset{\circ}{.}537$ | $-0\overset{\circ}{.}004\cdot T$ | $+0\overset{\circ}{.}407\cdot T$ |
| Uranus: | $+257\overset{\circ}{.}311$ | $+1\overset{\circ}{.}429\cdot T$ | $-15\overset{\circ}{.}175$ | $-0\overset{\circ}{.}114\cdot T$ | ||
| Neptun: | $+299\overset{\circ}{.}36$ | $+0\overset{\circ}{.}70\cdot\sin (\color{#ff00ff}{N})$ | $+0\overset{\circ}{.}849\cdot T$ | $+43\overset{\circ}{.}46$ | $-0\overset{\circ}{.}51\cdot\cos (\color{#ff00ff}{N})$ | $+0\overset{\circ}{.}242\cdot T$ |
mit $\color{#ff00ff}N = 357\overset{\circ}{.}85 + 52\overset{\circ}{.}316\cdot T$.
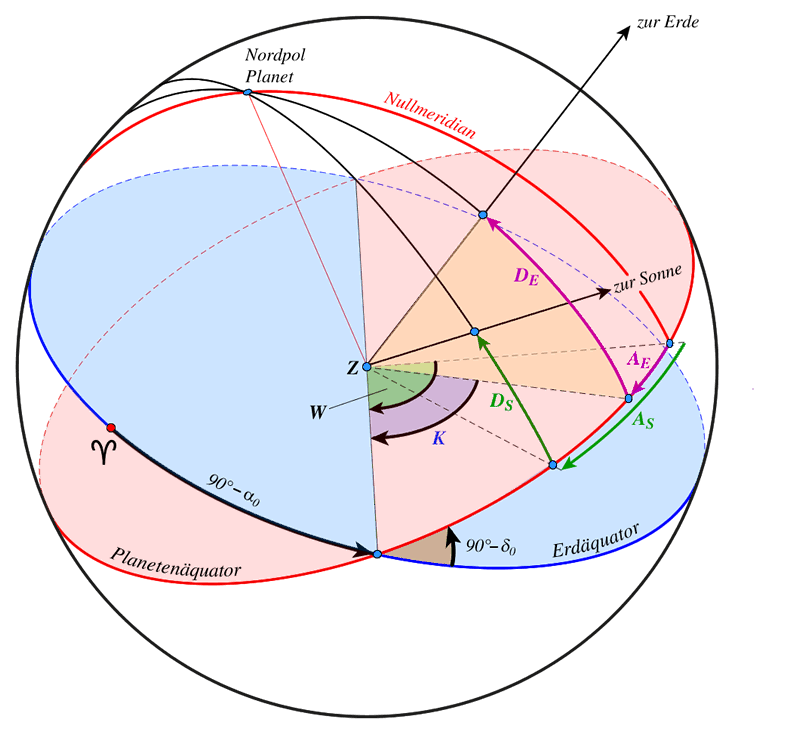
Die Rotationselemente $\alpha_0$ und $\delta_0$ bezeichnen die erdäquatoriale Lage der Rotationsachsen der Planeten. Es folgt die Tabelle mit den Nullmeridianen $W$:
| Tabelle 4 | ||||
|---|---|---|---|---|
| Planet | System | $W_0$ | $\text{d}W$ | $\Delta W$ |
| Sonne: | $+84\overset{\circ}{.}182$ | $+14\overset{\circ}{.}1844$ | $+1\overset{\circ}{.}222$ | |
| Merkur: | $+329\overset{\circ}{.}68$ | $+6\overset{\circ}{.}1385025$ | $+1\overset{\circ}{.}145$ | |
| Venus: | $+160\overset{\circ}{.}20$ | $-1\overset{\circ}{.}4813688$ | $+1\overset{\circ}{.}436$ | |
| Erde: | $+190\overset{\circ}{.}147$ | $+360\overset{\circ}{.}9856235$ | $+0\overset{\circ}{.}624$ | |
| Mars: | $+176\overset{\circ}{.}630$ | $+350\overset{\circ}{.}89198226$ | $+0\overset{\circ}{.}620$ | |
| Jupiter: | System I: | $+67\overset{\circ}{.}10$ | $+877\overset{\circ}{.}9$ | $+1\overset{\circ}{.}291$ |
| System II: | $+43\overset{\circ}{.}30$ | $+870\overset{\circ}{.}27$ | $+1\overset{\circ}{.}291$ | |
| System III: | $+284\overset{\circ}{.}95$ | $+870\overset{\circ}{.}5366420$ | $+1\overset{\circ}{.}291$ | |
| Saturn: | System I: | $+227\overset{\circ}{.}2037$ | $+844\overset{\circ}{.}3$ | $+3\overset{\circ}{.}470$ |
| System II: | $+105\overset{\circ}{.}4857$ | $+812\overset{\circ}{.}0$ | $+3\overset{\circ}{.}470$ | |
| System III: | $+38\overset{\circ}{.}90$ | $+810\overset{\circ}{.}7939024$ | $+3\overset{\circ}{.}470$ | |
| Uranus: | $+203\overset{\circ}{.}81$ | $-501\overset{\circ}{.}1600928$ | $+0\overset{\circ}{.}564$ | |
| Neptun: | $+253\overset{\circ}{.}18$ | $+536\overset{\circ}{.}3128492$ | $+0\overset{\circ}{.}662$ | |
Der Nullmeridian ist ein willkürlicher, aber festgelegter Wert auf der Oberfläche des Planeten. Er berechnet sich mit
$$W = W_0 + \textrm{d}W \cdot T + \Delta W\tag{14}$$
Die hier präsentierten Rotationselemente haben nur einen begrenzten Gültigkeitszeitraum. In einem eigenen Beitrag wird die Situation näher illustriert.
\(\begin{align} \cos(D_E) \cdot \cos(K) =&\, x = +\cos(\delta) \cdot \sin(\alpha_0 - \alpha) \\ \cos(D_E) \cdot \sin(K) =&\, y = +\cos(\delta) \cdot \cos(\alpha_0 - \alpha) \cdot \sin(\delta_0) - \sin(\delta) \cdot \cos(\delta_0) \\ \sin(D_E) =&\, z = -\cos(\delta) \cdot \cos(\alpha_0 - \alpha) \cdot \cos(\delta_0) - \sin(\delta) \cdot \sin(\delta_0) \end{align}\tag{15}\)
$D_E$ ist die planetozentrische Breite der Erde über dem planetaren Äquator. Damit ergibt sich planetozentrische Länge der Erde $A_E$ vom Nullmeridian des Planeten. $$A_E = (W - K)\cdot \text{sgn}\left(\frac{\textrm{d}W}{\textrm{d}T}\right)\tag{16}$$
Die Signum-Funktion stammt aus dem Abschnitt über die Vorzeichenfunktion. Die Auflösung der kartesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Man erhält die planetozentrisch äquatorialen Koordinaten $A_E$ (Länge) und $D_E$ (Breite) der Erde vom Planeten aus gesehen.
 Abb. 7
Abb. 7
\(\begin{align} \cos(D_E) \cdot \cos(P) =&\, x = -\cos(\delta_0) \cdot \cos(\alpha_0 - \alpha) \cdot \sin(\delta) + \cos(\delta) \cdot \sin(\delta_0) \\ \cos(D_E) \cdot \sin(P) =&\, y = +\cos(\delta_0) \cdot \sin(\alpha_0 - \alpha) \\ \sin(D_E) =&\, z = -\cos(\delta) \cdot \cos(\alpha_0 - \alpha) \cdot \cos(\delta_0) - \sin(\delta) \cdot \sin(\delta_0) \end{align}\tag{17}\)
$D_E$ ist wieder die planetozentrische Breite der Erde. Die Auflösung der kartesischen Koordinaten erfolgt im Abschnitt über sphärische Koordinaten. Man erhält den Positionswinkel der planetaren Rotationsachse $P$.
Die Rotationselemente (samt Nullmeridian) stammen aus dem Explanatory Supplement und aus dem Report der IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites. Der Nullmeridian für das System III Jupiters und für das System II Saturns stammen von K.H. Bücke; siehe auch die Literaturhinweise.
- System I: Rotation im Bereich des Äquators im Bereich zwischen 10° nördlich und südlich des Äquators.
- System II: Rotation nördlich des nördlichen Äquatorialbandes und südlich des südlichen Äquatorialbandes. Hier sind die Polarregionen gemeint.
- System III: Rotation von Radiostrahlungsemissionen und der Magnetfelder, die im Gegensatz zu System I und II ortsfest lokalisiert sind.
Die hier präsentierten Rotationselemente der Planeten haben nur einen begrenzten Gültigkeitszeitraum. In einem eigenen Beitrag wird die Situation näher illustriert.
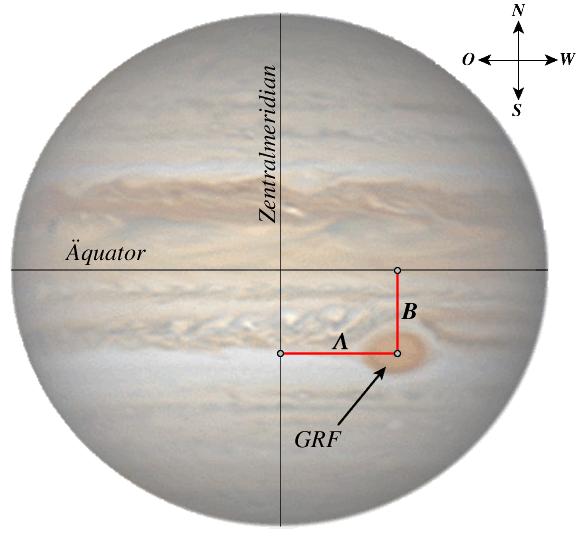
Der große, rote Fleck Jupiters
Das gewaltige Hochdrucksystem besteht schon seit Jahrhunderten und ist reizvoll zu beobachten.
Die jovigraphische Länge $\Lambda$ wird westwärts gezählt. Liegt diese zwischen $90^{\circ}$ und $270^{\circ}$, so befindet sich der GRF auf der erdabgewandten Seite des Jupiter. Die jovigraphische Breite $B$ liegt nahezu konstant bei $-22\overset{\circ}{.}5$. Zieht man die planetozentrische Länge $A_E$ der Erde (Jupiters Zentralmeridian) von der aktuellen Länge $S$ ab,
$$\Lambda = \textrm{red}(S - A_E;360^{\circ})\tag{18}$$
so bekommt man die derzeitige und ungefähre Lage des großen, roten Flecks $\Lambda$. Die Transitzeiten sind dann: $$JDE = 2451545.0 + \frac{\Lambda}{dW} - \tau\tag{19}$$
mit der Reduktionsfunktion, der Lichtlaufzeit $\tau$ und $dW = 870\overset{\circ}{.}1869147$ als der synodischen Rotation Jupiters im System II. $S$ erhält man aus der nachfolgenden Tabelle 5:
| Tabelle 5: Jovigraphische Länge des großen, roten Flecks | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Zeit | $S$ | Zeit | $S$ | Zeit | $S$ | Zeit | $S$ | Zeit | $S$ | Zeit | $S$ |
| 1986.10 | 19$^{\circ}$ | 1998.01 | 64$^{\circ}$ | 2004.03 | 89$^{\circ}$ | 2010.06 | 150$^{\circ}$ | 2015.12 | 238$^{\circ}$ | 2021.05 | 357$^{\circ}$ |
| 1986.11 | 19$^{\circ}$ | 1998.09 | 65$^{\circ}$ | 2004.04 | 89$^{\circ}$ | 2010.07 | 153$^{\circ}$ | 2016.01 | 239$^{\circ}$ | 2021.06 | 359$^{\circ}$ |
| 1987.11 | 14$^{\circ}$ | 1998.10 | 62$^{\circ}$ | 2004.10 | 94$^{\circ}$ | 2010.08 | 155$^{\circ}$ | 2016.02 | 240$^{\circ}$ | 2021.07 | 0$^{\circ}$ |
| 1987.12 | 14$^{\circ}$ | 1998.11 | 62$^{\circ}$ | 2004.11 | 94$^{\circ}$ | 2010.09 | 156$^{\circ}$ | 2016.03 | 243$^{\circ}$ | 2021.08 | 0$^{\circ}$ |
| 1988.01 | 14$^{\circ}$ | 1998.12 | 64$^{\circ}$ | 2004.12 | 94$^{\circ}$ | 2010.10 | 158$^{\circ}$ | 2016.04 | 246$^{\circ}$ | 2021.09 | 2$^{\circ}$ |
| 1988.11 | 16$^{\circ}$ | 1999.01 | 64$^{\circ}$ | 2005.01 | 94$^{\circ}$ | 2010.11 | 159$^{\circ}$ | 2016.05 | 246$^{\circ}$ | 2021.10 | 4$^{\circ}$ |
| 1988.12 | 16$^{\circ}$ | 1999.02 | 64$^{\circ}$ | 2005.02 | 94$^{\circ}$ | 2010.12 | 160$^{\circ}$ | 2016.06 | 248$^{\circ}$ | 2021.11 | 5$^{\circ}$ |
| 1989.01 | 16$^{\circ}$ | 1999.06 | 66$^{\circ}$ | 2005.03 | 98$^{\circ}$ | 2011.01 | 163$^{\circ}$ | 2016.07 | 250$^{\circ}$ | 2021.12 | 6$^{\circ}$ |
| 1989.02 | 16$^{\circ}$ | 1999.08 | 66$^{\circ}$ | 2005.04 | 98$^{\circ}$ | 2011.02 | 164$^{\circ}$ | 2016.08 | 252$^{\circ}$ | 2022.01 | 9$^{\circ}$ |
| 1989.03 | 16$^{\circ}$ | 1999.09 | 66$^{\circ}$ | 2005.05 | 98$^{\circ}$ | 2011.05 | 166$^{\circ}$ | 2016.12 | 258$^{\circ}$ | 2022.02 | 10$^{\circ}$ |
| 1989.11 | 30$^{\circ}$ | 1999.10 | 66$^{\circ}$ | 2005.06 | 98$^{\circ}$ | 2011.06 | 167$^{\circ}$ | 2017.01 | 262$^{\circ}$ | 2022.04 | 14$^{\circ}$ |
| 1989.12 | 30$^{\circ}$ | 1999.11 | 66$^{\circ}$ | 2005.07 | 98$^{\circ}$ | 2011.07 | 168$^{\circ}$ | 2017.02 | 263$^{\circ}$ | 2022.05 | 16$^{\circ}$ |
| 1990.01 | 30$^{\circ}$ | 1999.12 | 66$^{\circ}$ | 2005.08 | 98$^{\circ}$ | 2011.08 | 168$^{\circ}$ | 2017.03 | 264$^{\circ}$ | 2022.06 | 17$^{\circ}$ |
| 1990.02 | 22$^{\circ}$ | 2000.01 | 66$^{\circ}$ | 2005.09 | 98$^{\circ}$ | 2011.09 | 169$^{\circ}$ | 2017.04 | 267$^{\circ}$ | 2022.07 | 21$^{\circ}$ |
| 1990.04 | 22$^{\circ}$ | 2000.02 | 66$^{\circ}$ | 2005.11 | 104$^{\circ}$ | 2011.10 | 172$^{\circ}$ | 2017.05 | 270$^{\circ}$ | 2022.08 | 22$^{\circ}$ |
| 1990.12 | 27$^{\circ}$ | 2000.03 | 66$^{\circ}$ | 2005.12 | 104$^{\circ}$ | 2011.11 | 171$^{\circ}$ | 2017.06 | 271$^{\circ}$ | 2022.09 | 23$^{\circ}$ |
| 1991.01 | 27$^{\circ}$ | 2000.04 | 74$^{\circ}$ | 2006.04 | 104$^{\circ}$ | 2011.12 | 173$^{\circ}$ | 2017.07 | 274$^{\circ}$ | 2022.10 | 26$^{\circ}$ |
| 1991.02 | 27$^{\circ}$ | 2000.05 | 74$^{\circ}$ | 2006.05 | 109$^{\circ}$ | 2012.01 | 175$^{\circ}$ | 2017.08 | 276$^{\circ}$ | 2022.11 | 26$^{\circ}$ |
| 1991.03 | 27$^{\circ}$ | 2000.06 | 74$^{\circ}$ | 2006.06 | 109$^{\circ}$ | 2012.02 | 175$^{\circ}$ | 2017.09 | 278$^{\circ}$ | 2022.12 | 29$^{\circ}$ |
| 1991.04 | 32$^{\circ}$ | 2000.07 | 74$^{\circ}$ | 2006.07 | 114$^{\circ}$ | 2012.03 | 176$^{\circ}$ | 2017.10 | 280$^{\circ}$ | 2023.01 | 31$^{\circ}$ |
| 1991.05 | 32$^{\circ}$ | 2000.08 | 74$^{\circ}$ | 2006.08 | 114$^{\circ}$ | 2012.03 | 177$^{\circ}$ | 2017.11 | 281$^{\circ}$ | 2023.02 | 31$^{\circ}$ |
| 1991.06 | 32$^{\circ}$ | 2000.09 | 74$^{\circ}$ | 2006.10 | 113$^{\circ}$ | 2012.07 | 181$^{\circ}$ | 2017.12 | 283$^{\circ}$ | 2023.03 | 32$^{\circ}$ |
| 1992.02 | 34$^{\circ}$ | 2000.10 | 74$^{\circ}$ | 2006.11 | 112$^{\circ}$ | 2012.08 | 182$^{\circ}$ | 2018.01 | 285$^{\circ}$ | 2023.05 | 35$^{\circ}$ |
| 1992.03 | 34$^{\circ}$ | 2000.12 | 74$^{\circ}$ | 2006.12 | 112$^{\circ}$ | 2012.09 | 183$^{\circ}$ | 2018.02 | 286$^{\circ}$ | 2023.06 | 38$^{\circ}$ |
| 1992.04 | 30$^{\circ}$ | 2001.01 | 76$^{\circ}$ | 2007.01 | 114$^{\circ}$ | 2012.10 | 185$^{\circ}$ | 2018.03 | 288$^{\circ}$ | 2023.07 | 39${^\circ}$ |
| 1992.05 | 30$^{\circ}$ | 2001.02 | 76$^{\circ}$ | 2007.02 | 116$^{\circ}$ | 2012.11 | 187$^{\circ}$ | 2018.04 | 289$^{\circ}$ | 2023.08 | 39${^\circ}$ |
| 1992.06 | 33$^{\circ}$ | 2001.03 | 76$^{\circ}$ | 2007.03 | 117$^{\circ}$ | 2012.12 | 188$^{\circ}$ | 2018.05 | 289$^{\circ}$ | 2023.09 | 41${^\circ}$ |
| 1992.07 | 33$^{\circ}$ | 2001.04 | 76$^{\circ}$ | 2007.04 | 117$^{\circ}$ | 2013.01 | 190$^{\circ}$ | 2018.06 | 289$^{\circ}$ | 2023.10 | 44${^\circ}$ |
| 1993.02 | 38$^{\circ}$ | 2001.05 | 76$^{\circ}$ | 2007.05 | 119$^{\circ}$ | 2013.02 | 191$^{\circ}$ | 2018.07 | 291$^{\circ}$ | 2023.11 | 45$^{\circ}$ |
| 1993.03 | 38$^{\circ}$ | 2001.08 | 76$^{\circ}$ | 2007.06 | 120$^{\circ}$ | 2013.03 | 192$^{\circ}$ | 2018.08 | 292$^{\circ}$ | 2023.12 | 46$^{\circ}$ |
| 1993.04 | 35$^{\circ}$ | 2001.09 | 76$^{\circ}$ | 2007.07 | 122$^{\circ}$ | 2013.04 | 193$^{\circ}$ | 2018.09 | 293$^{\circ}$ | 2024.01 | 49$^{\circ}$ |
| 1993.05 | 35$^{\circ}$ | 2001.10 | 76$^{\circ}$ | 2007.08 | 124$^{\circ}$ | 2013.05 | 195$^{\circ}$ | 2018.10 | 294$^{\circ}$ | 2024.02 | 50$^{\circ}$ |
| 1993.06 | 35$^{\circ}$ | 2001.11 | 76$^{\circ}$ | 2007.09 | 123$^{\circ}$ | 2013.08 | 199$^{\circ}$ | 2019.01 | 302$^{\circ}$ | 2024.03 | 52$^{\circ}$ |
| 1993.07 | 45$^{\circ}$ | 2001.12 | 77$^{\circ}$ | 2007.10 | 123$^{\circ}$ | 2013.09 | 201$^{\circ}$ | 2019.02 | 303$^{\circ}$ | 2024.04 | 53$^{\circ}$ |
| 1993.08 | 45$^{\circ}$ | 2002.01 | 77$^{\circ}$ | 2008.02 | 123$^{\circ}$ | 2013.10 | 203$^{\circ}$ | 2019.03 | 308$^{\circ}$ | 2024.06 | 56$^{\circ}$ |
| 1994.02 | 45$^{\circ}$ | 2002.02 | 77$^{\circ}$ | 2008.03 | 123$^{\circ}$ | 2013.11 | 204$^{\circ}$ | 2019.04 | 310$^{\circ}$ | 2024.07 | 57$^{\circ}$ |
| 1994.03 | 45$^{\circ}$ | 2002.03 | 77$^{\circ}$ | 2008.04 | 124$^{\circ}$ | 2013.12 | 206$^{\circ}$ | 2019.05 | 310$^{\circ}$ | 2024.08 | 58$^{\circ}$ |
| 1994.04 | 49$^{\circ}$ | 2002.04 | 80$^{\circ}$ | 2008.05 | 126$^{\circ}$ | 2014.01 | 207$^{\circ}$ | 2019.06 | 312$^{\circ}$ | 2024.09 | 59$^{\circ}$ |
| 1994.06 | 40$^{\circ}$ | 2002.05 | 80$^{\circ}$ | 2008.06 | 125$^{\circ}$ | 2014.02 | 208$^{\circ}$ | 2019.07 | 313$^{\circ}$ | 2024.10 | 62$^{\circ}$ |
| 1994.07 | 40$^{\circ}$ | 2002.06 | 80$^{\circ}$ | 2008.07 | 127$^{\circ}$ | 2014.03 | 209$^{\circ}$ | 2019.08 | 315$^{\circ}$ | 2024.11 | 63$^{\circ}$ |
| 1994.08 | 40$^{\circ}$ | 2002.07 | 80$^{\circ}$ | 2008.08 | 128$^{\circ}$ | 2014.04 | 212$^{\circ}$ | 2019.09 | 316$^{\circ}$ | 2024.12 | 65$^{\circ}$ |
| 1994.09 | 40$^{\circ}$ | 2002.08 | 80$^{\circ}$ | 2008.09 | 128$^{\circ}$ | 2014.05 | 213$^{\circ}$ | 2019.10 | 319$^{\circ}$ | 2025.01 | 68$^{\circ}$ |
| 1995.04 | 42$^{\circ}$ | 2002.09 | 80$^{\circ}$ | 2008.10 | 130$^{\circ}$ | 2014.09 | 216$^{\circ}$ | 2019.11 | 320$^{\circ}$ | 2025.02 | 68$^{\circ}$ |
| 1995.05 | 42$^{\circ}$ | 2002.10 | 80$^{\circ}$ | 2008.11 | 130$^{\circ}$ | 2014.10 | 219$^{\circ}$ | 2020.02 | 325$^{\circ}$ | 2025.03 | 70$^{\circ}$ |
| 1995.06 | 42$^{\circ}$ | 2002.11 | 80$^{\circ}$ | 2009.03 | 132$^{\circ}$ | 2014.11 | 220$^{\circ}$ | 2020.03 | 328$^{\circ}$ | 2025.04 | 72$^{\circ}$ |
| 1995.07 | 42$^{\circ}$ | 2002.12 | 80$^{\circ}$ | 2009.04 | 133$^{\circ}$ | 2014.12 | 221$^{\circ}$ | 2020.04 | 331$^{\circ}$ | 2025.05 | 73$^{\circ}$ |
| 1995.08 | 42$^{\circ}$ | 2003.01 | 80$^{\circ}$ | 2009.05 | 135$^{\circ}$ | 2015.01 | 223$^{\circ}$ | 2020.05 | 332$^{\circ}$ | 2025.08 | 75$^{\circ}$ |
| 1995.09 | 42$^{\circ}$ | 2003.02 | 80$^{\circ}$ | 2009.06 | 135$^{\circ}$ | 2015.02 | 223$^{\circ}$ | 2020.06 | 336$^{\circ}$ | 2025.09 | 76$^{\circ}$ |
| 1995.10 | 49$^{\circ}$ | 2003.03 | 80$^{\circ}$ | 2009.07 | 137$^{\circ}$ | 2015.03 | 225$^{\circ}$ | 2020.07 | 338$^{\circ}$ | 2025.10 | 78$^{\circ}$ |
| 1995.11 | 49$^{\circ}$ | 2003.04 | 84$^{\circ}$ | 2009.08 | 138$^{\circ}$ | 2015.04 | 227$^{\circ}$ | 2020.08 | 340$^{\circ}$ | 2025.11 | 76$^{\circ}$ |
| 1996.08 | 51$^{\circ}$ | 2003.05 | 84$^{\circ}$ | 2009.09 | 139$^{\circ}$ | 2015.05 | 226$^{\circ}$ | 2020.09 | 343$^{\circ}$ | 2025.12 | 79$^{\circ}$ |
| 1996.09 | 51$^{\circ}$ | 2003.06 | 84$^{\circ}$ | 2009.10 | 141$^{\circ}$ | 2015.06 | 227$^{\circ}$ | 2020.10 | 345$^{\circ}$ | 2026.01 | 81$^{\circ}$ |
| 1996.10 | 51$^{\circ}$ | 2003.07 | 84$^{\circ}$ | 2009.11 | 142$^{\circ}$ | 2015.08 | 232$^{\circ}$ | 2020.11 | 346$^{\circ}$ | 2026.02 | 81$^{\circ}$ |
| 1996.11 | 61$^{\circ}$ | 2003.11 | 84$^{\circ}$ | 2009.12 | 142$^{\circ}$ | 2015.09 | 231$^{\circ}$ | 2020.12 | 348$^{\circ}$ | ||
| 1996.12 | 61$^{\circ}$ | 2003.12 | 84$^{\circ}$ | 2010.04 | 148$^{\circ}$ | 2015.10 | 234$^{\circ}$ | 2021.03 | 354$^{\circ}$ | ||
| 1997.09 | 61$^{\circ}$ | 2004.01 | 84$^{\circ}$ | 2010.05 | 149$^{\circ}$ | 2015.11 | 235$^{\circ}$ | 2021.04 | 356$^{\circ}$ | ||
Die Tabelle stammt von JUPOS.org und wird laufend ca. alle 1½ Monate aktualisiert. Der aktuelle Stand ist Freitag, der 30. Januar 2026. Die vermutlich nächste Aktualisierung findet am Freitag, den 20. März 2026 statt.
Saturns Schatten auf seinen Ringen
Bei einer genauen Beobachtung des Saturn fällt auf, dass der Schatten des Planeten auf seinen Ringen sich vor der Opposition leicht westlich vom Planeten befindet, nach der Opposition etwas östlich. Der Ring ist dann an dieser Stelle nicht sichtbar. Es handelt sich nur um einen wenige Bogensekunden breiter Bereich der Sichtbarkeit des Schattens. Einen ersten Hinweis auf den Schattenwurf liefert auch der Beleuchtungsdefekt $d''$. K.H. Bücke beschrieb 1990 erstmalig dieses Phänomen im Mitteilungen für Planetenbeobachter.
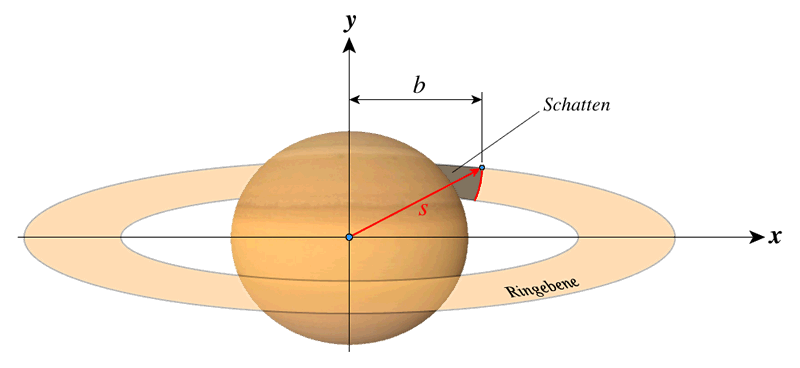 Abb. 9: Saturns Schatten (Erdansicht)
Abb. 9: Saturns Schatten (Erdansicht)
Der Wert $b$ schwankt zwischen Eins und Null bei einer planetozentrischen Deklination $D_E$ zwischen Null (Durchgang durch die Ringebene) bzw. $23\overset{\circ}{.}66$. Bei größerer Öffnung erreicht $b$ komplexe Werte. Der Schatten liegt dann hinter dem Planeten. Der Ringabstand $s$ liegt in der Ringebene. Der Halbmesser $b$ des Schattens auf der Ringebene lautet: $$b = \sqrt{1 - \frac{s^2 \cdot \sin^2(D_S)}{1 - \epsilon \cdot \cos^2(D_S)}}$$
Es handelt sich um den am weitesten vom Saturn entfernten Punkt des Terminators (Abb. 8). $s$ ist der Ringabstand in Planetenradien und reicht laut K.H. Bücke von 1.509 bis 2.269. Mit $\epsilon = 0.2037$ ist hier die numerische Exzentrizität des Saturnkörpers (Abplattung) gemeint. Der scheinbare Poldurchmesser $\varnothing_P$ (in Bogensekunden) berechnet sich mit $$\varnothing_P = \varnothing\cdot \sqrt{1 - \epsilon\cdot\cos^2(D_E)}$$
Nun wird der modifizierte Phasenwinkel $\psi$ gesucht: $$\psi(s) = \Delta A + \gamma \qquad \text{mit} \qquad \gamma = \arcsin\left(\frac{b}{s}\right)$$
Er dient zur Berechnung der Koordinaten $x(s)$, $y(s)$ auf der Projektionsebene.
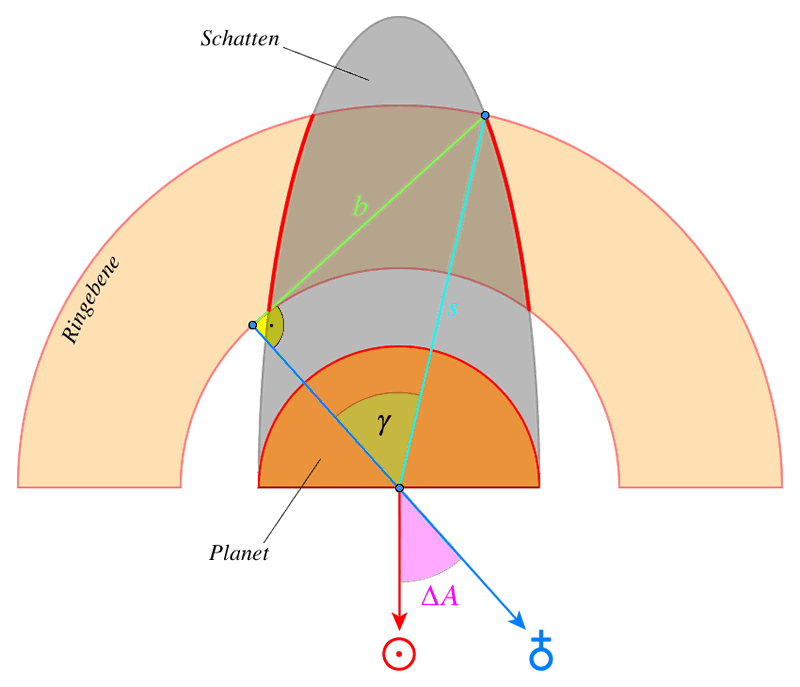 Abb. 10: Saturns Schatten von oben
Abb. 10: Saturns Schatten von oben
Die Ansicht von oberhalb des Saturn. Der Schattenhalbmesser $b$ steht senkrecht auf der Sichtlinie zur Erde. Der Abstand der Schattengrenze $s$ erstreckt sich von dem Zentrum des Planeten bis zum Terminator auf der Ringbene. Der Winkel $\gamma$ ist nicht die Längendifferenz $\Delta$A der Zentralmeridiane, sondern der Winkel zwischen der Schattengrenze und der Erdposition. $\Delta$A = A$_E$ $-$ A$_S$ sind die planetozentrischen Längen der Erde bzw. der Sonne (Abb. 9). $\Delta$A kann in erster Näherung durch den Phasenwinkel $\varphi$ ersetzt werden. Daraus resultieren die Koordinaten als Funktionen von $s$ für die Schattengrenze in Abb. 8: \[\begin{split} x(s) &= s \cdot \varnothing \cdot \sin(\psi(s)) \\ y(s) &= s \cdot \varnothing \cdot \cos(\psi(s)) \cdot \sin(D_E) \end{split}\]
$A_E$, $D_E$ = planetozentrische Koordinaten der Erde
$\gamma$ = Winkel zwischen Schattengrenze und Erdposition
$A_S$, $D_S$ = planetozentrische Koordinaten der Sonne
$\varnothing$ = scheinbarer Äquatordurchmesser
$\Delta A$ = Längendifferenz der Zentralmeridiane
$\varnothing_P$ = scheinbarer Poldurchmesser
$x(s)$, $y(s)$ = Koordinaten der Schattengrenze
$s$ = Abstand im Ringbereich
$\psi$(s) = modifizierter Phasenwinkel
$b$ = Schattenhalbmesser