Inhaltsverzeichnis
Die Monde der Planeten
Dieses Kapitel ist ein Novum im Internet. Es ist der erste Abschnitt über die Berechnung der hellsten Planetenmonde. Herangezogen werden die Ephemeriden von Hempe & Molt (Jupiter I), J. Meeus (Jupiter II) für die Jupitermonde Io, Europa, Ganymed und Kallisto und Dan Bruton (Saturn I) und K.H. Bücke (Saturn II) für die Saturnmonde Tethys, Dione, Rhea, Titan und Japetus. Alle Monde haben synodische Umlaufszeiten. Nur Saturn II verwendet siderische Umlaufszeiten.
Jupiter
Jupiter I
Diese Theorie setzt voraus, dass die Mondbahnen kreisförmig sind und mit dem Jupiteräquator zusammenfallen. Die Epoche ist 1900 Januar 0.5 und das Äquinoktium ist $J1900.0$. Die Umlaufszeiten sind synodisch.
$$\color{#cc0000}{d = JDE − 2415020.0}\tag{1}$$
| Tabelle 1 | ||
|---|---|---|
| Mond: | Radius: | mittlere Länge: |
| Io: | $r_1 = 5.906$ | $l_1 = 84\overset{\circ}{.}55061 + 203\overset{\circ}{.}405863 \cdot (d - \tau) + \varphi - C$ |
| Europa: | $r_2 = 9.397$ | $l_2 = 41\overset{\circ}{.}50155 + 101\overset{\circ}{.}291632 \cdot (d - \tau) + \varphi - C$ |
| Ganymed: | $r_3 = 14.989$ | $l_3 = 109\overset{\circ}{.}97702 + 50\overset{\circ}{.}2345169 \cdot (d - \tau) + \varphi - C$ |
| Kallisto: | $r_4 = 26.364$ | $l_4 = 176\overset{\circ}{.}35864 + 21\overset{\circ}{.}4879802 \cdot (d - \tau) + \varphi - C$ |
Jupiter II
Es gilt wieder für die mittlere tägliche Bewegung die synodische Umlaufszeit. Die Längen l$_k$ der Jupitermonde Io (1), Europa (2), Ganymed (3) und Kallisto (4) sind dann:
$$\color{#cc0000}{d = JDE − 2451545.0}\tag{2}$$
| Tabelle 2 | |
|---|---|
| Mond: | mittlere Länge: |
| Io: | $l_1 = 163\overset{\circ}{.}8069 + 203\overset{\circ}{.}4058646 \cdot (d - \tau) + \varphi - C$ |
| Europa: | $l_2 = 358\overset{\circ}{.}4140 + 101\overset{\circ}{.}2916335 \cdot (d - \tau) + \varphi - C$ |
| Ganymed: | $l_3 = 5\overset{\circ}{.}7176 + 50\overset{\circ}{.}2345180 \cdot (d - \tau) + \varphi - C$ |
| Kallisteo: | $l_4 = 224\overset{\circ}{.}8092 + 21\overset{\circ}{.}4879800 \cdot (d - \tau) + \varphi - C$ |
$$G = 331\overset{\circ}{.}18 + 50\overset{\circ}{.}310482 \cdot (d - \tau)\tag{3}$$ $$H = 87\overset{\circ}{.}45 + 21\overset{\circ}{.}569231 \cdot (d - \tau)\tag{4}$$
Zu $l_k$ werden dann die Korrekturen G und H hinzuaddiert. Die Radiusvektoren $r_k$ und die korrigierten Längen $l_k'$ der einzelnen Satelliten sind:
| Tabelle 3 | ||
|---|---|---|
| Mond: | Radius: | mittlere Länge: |
| Io: | $r_1 = 5.9057 - 0.0244 \cdot \cos(2 (l_1 - l_2))$ | $l_1' = l_1 + 0\overset{\circ}{.}473 \cdot \sin(2 (l_1 - l_2))$ |
| Europa: | $r_2 = 9.3966 - 0.0882 \cdot \cos(2 (l_2 - l_3))$ | $l_2' = l_2 + 1\overset{\circ}{.}065 \cdot \sin(2 (l_2 - l_3))$ |
| Ganymed: | $r_3 = 14.9833 - 0.0216 \cdot \cos(G)$ | $l_3' = l_3 + 0\overset{\circ}{.}165 \cdot \sin(G)$ |
| Kallisto: | $r_4 = 26.3627 - 0.1939 \cdot \cos(H)$ | $l_4' = l_4 + 0\overset{\circ}{.}843 \cdot \sin(H)$ |
Es werden weiter unten dann $l_k'$ statt $l_k$ eingesetzt.
Saturn
Saturn I
Es wird ein Zusammenfallen aller kreisförmigen Mondbahnen (bis auf Japetus) mit dem Saturnäquator postuliert. Die Epoche ist 1980 Januar 0.5 und das Äquinoktium ist $J1980.0$. Die Umlaufszeiten sind synodisch.
$$\color{#cc0000}{d = JDE − 2444238.5}\tag{5}$$
| Tabelle 4 | ||
|---|---|---|
| Mond: | Radius: | mittlere Länge: |
| Tethys: | $r_1 = 4.8898$ | $l_1 = 172\overset{\circ}{.}8546 + 190\overset{\circ}{.}668614452\cdot (d - \tau) + \varphi - C$ |
| Dione: | $r_2 = 6.2637$ | $l_2 = 76\overset{\circ}{.}8438 + 131\overset{\circ}{.}505802072\cdot (d - \tau) + \varphi - C$ |
| Rhea: | $r_3 = 8.7476$ | $l_3 = 37\overset{\circ}{.}2555 + 79\overset{\circ}{.}6607672779\cdot (d - \tau) + \varphi - C$ |
| Titan: | $r_4 = 20.2695$ | $l_4 = 57\overset{\circ}{.}7005 + 22\overset{\circ}{.}54663941461\cdot (d - \tau) + \varphi - C$ |
| Japetus: | $r_5 = 59.0712$ | $l_5 = 195\overset{\circ}{.}3513 + 4\overset{\circ}{.}5045597067\cdot (d - \tau) + \varphi - C$ |
Spezialfall Japetus:
Die Neigung $\gamma$ der Japetusbahn zum Saturnäquator (Ringebene) ist gegeben mit:
\[\begin{align} \sin(\gamma) = &+\cos(\delta) \cdot \Big[\cos(83\overset{\circ}{.}51) \cdot \sin(40\overset{\circ}{.}27- \alpha) \cdot\\ &\cdot\sin(75\overset{\circ}{.}6)\sin(\alpha - 320\overset{\circ}{.}1) \cdot \cos(75\overset{\circ}{.}6) \cdot \sin(83\overset{\circ}{.}51)\Big]\\ &+\sin(\delta) \cdot \cos(83\overset{\circ}{.}51) \cdot \cos(75\overset{\circ}{.}6) \cdot \sin(320\overset{\circ}{.}1 - 40\overset{\circ}{.}27) \end{align}\tag{6}\]
\[\begin{align} \sin(V) =& - \cos(75\overset{\circ}{.}6)\cdot \cos(320\overset{\circ}{.}1- \alpha)\cdot \cos(\delta)\\ &- \sin(75\overset{\circ}{.}6)\cdot \sin(\delta) \end{align}\tag{7}\]
\[\tan(U) = \dfrac{\sin(\delta_0)\cdot \cos(\alpha_0 - \alpha) - \cos(\delta_0)\cdot \tan(\delta)} {\sin(\alpha_0 - \alpha)}\tag{8}\]
mit den planetozentrisch planetoäquatorialen Koordinaten der Japetusbahn:
$$\alpha_0 = 318\overset{\circ}{.}16 − 3\overset{\circ}{.}949\cdot T\tag{9}$$ $$\delta_0 = 75\overset{\circ}{.}03 − 1\overset{\circ}{.}143\cdot T\tag{10}$$ und $$T = \frac{JDE - 2451545}{36525}\tag{11}$$
Bei $U$ ist auf die quadrantentreue Wiedergabe zu achten.
$V$ ist die planetozentrische Breite der Erde auf der Mondbahn.
$U$ ist die planetozentrische Länge der Erde auf der Mondbahn.
$\alpha$, $\delta$ = geozentrisch äquatoriale Koordinaten des Saturn.
Saturn II
Es gilt allein in diesem Abschnitt für die mittlere tägliche Bewegung die siderische Umlaufszeit. Zuerst braucht man die mittleren Anomalien und die Radien von Titan und Japetus.
$$\color{#cc0000}{d = JD - 2451545.0}\tag{12}$$
\[\begin{align} dl_1 &= 2\overset{\circ}{.}065 \cdot \sin(0\overset{\circ}{.}013926 (d - 2857.2))\\ M_4 &= 163\overset{\circ}{.}7 + 22\overset{\circ}{.}575585 \cdot (d - \tau)\\ M_5 &= 207\overset{\circ}{.}7 + 4\overset{\circ}{.}537626 \cdot (d - \tau)\\ \nu_4 - M_4 &= 3\overset{\circ}{.}33 \cdot \sin(M_4) + 0\overset{\circ}{.}06 \cdot \sin(2 \ M_4)\\ \nu_5 - M_5 &= 3\overset{\circ}{.}24 \cdot \sin(M_5) + 0\overset{\circ}{.}06 \cdot \sin(2 \ M_5)\\ \Delta r_4 &= 20.38 - 0.593 \cdot \cos(M_4)\\ \Delta r_5 &= 59.39 - 1.679 \cdot \cos(M_5) - 0.024 \cdot \cos(2 \ M_5) \end{align}\tag{13}\]
$dl_1$ ist die Bahnstörung von Tethys. $\nu_k - M_k$ sind die Mittelpunktsgleichungen von Titan und Japetus (nicht zu verwechseln mit den Mittelpunktsgleichungen von Saturn C). $M_4$ und $M_5$ sind die mittleren Anomalien von Titan und Japetus. $\Delta r_k$ sind die korrespondierenden Korrekturen des Abstands vom Planeten. Die planetozentrische Länge K der Erde wird für die Saturnsatelliten gebraucht und muss als nächstes berechnet werden. Es gilt
$$\tan(K) = \left(\frac{\sin(\delta_0) \cdot \cos(\alpha_0 - \alpha) - \cos(\delta_0) \cdot \tan(\delta)}{\sin(\alpha_0 - \alpha)}\right)\tag{14}$$
mit $\alpha_0$, $\delta_0$ für Saturn, Tethys, Dione und Rhea. $\alpha$, $\delta$ sind die geozentrisch - äquatorialen Koordinaten Saturns. Für Titan und Japetus benötigt man separate Werte:
$$T = \frac{d}{36525}\tag{15}$$
| Tabelle 5 | |
|---|---|
| Titan: | $\alpha_0 = 36\overset{\circ}{.}41 - 0\overset{\circ}{.}036 \cdot T + 2\overset{\circ}{.}66 \cdot \sin(G)$ |
| $\delta_0 = 83\overset{\circ}{.}94 - 0\overset{\circ}{.}004 \cdot T - 0\overset{\circ}{.}30 \cdot \cos(G)$ | |
| Japetus: | $\alpha_0 = 318\overset{\circ}{.}16 - 3\overset{\circ}{.}949 \cdot T$ |
| $\delta_0 = 75\overset{\circ}{.}03 - 1\overset{\circ}{.}143 \cdot T$ | |
mit $G$ für Titan: $$G = 29\overset{\circ}{.}80 - 52\overset{\circ}{.}1 \cdot T\tag{16}$$
Setzt man in die Gleichung für K ein, so bekommt man $K_4$ bzw. $K_5$. Die Radiusvektoren $r_k$ und die Längen $l_k$ der Saturnmonde Tethys (1), Dione (2), Rhea (3), Titan (4) und Japetus (5) sind dann mit der planetozentrischen Länge K, $K_4$ und $K_5$:
| Tabelle 6 | ||
|---|---|---|
| Monde: | Radius: | mittlere Länge: |
| Tethys: | $r_1 = 4.91$ | $l_1 = 188\overset{\circ}{.}10 + 190\overset{\circ}{.}697813 \cdot (d - \tau) + dl_1 - K$ |
| Dione: | $r_2 = 6.29$ | $l_2 = 177\overset{\circ}{.}70 + 131\overset{\circ}{.}534888 \cdot (d - \tau) - K$ |
| Rhea: | $r_3 = 8.78$ | $l_3 = 52\overset{\circ}{.}23 + 79\overset{\circ}{.}689963 \cdot (d - \tau) - K$ |
| Titan: | $r_4 = \Delta r_4$ | $l_4 = 9\overset{\circ}{.}.62 + 22\overset{\circ}{.}576895 \cdot (d - \tau) + (\nu_4 - M_4) - K_4$ |
| Japetus: | $r_5 = \Delta r_5$ | $l_5 = 171\overset{\circ}{.}22 + 4\overset{\circ}{.}538088 \cdot (d - \tau) + (\nu_5 - M_5) - K_5$ |
Die Neigungen $D_4$ und $D_5$ der Titan- und Japetusbahnen zum Beobachter auf der Erde sind:
\[\begin{align} \sin(D_4) &= - \cos(83\overset{\circ}{.}69) \cdot \cos(37\overset{\circ}{.}77 - \alpha) \cdot \cos(\delta) - \sin(83\overset{\circ}{.}69) \cdot \sin(\delta)\\ \sin(D_5) &= - \cos(75\overset{\circ}{.}49) \cdot \cos(318\overset{\circ}{.}56 - \alpha) \cdot \cos(\delta) - \sin(75\overset{\circ}{.}49) \cdot \sin(\delta) \end{align}\tag{17}\]
\[\begin{align} \sin(\gamma_4) =& + \cos(\delta) \cdot \big[\cos(83\overset{\circ}{.}52 \cdot \sin(40\overset{\circ}{.}66 - \alpha) \cdot \sin(83\overset{\circ}{.}69^{\circ}) \\ &+ \sin(\alpha - 37\overset{\circ}{.}77) \cdot \cos(83\overset{\circ}{.}69) \cdot \sin(83\overset{\circ}{.}52)\big] \\ &+ \sin(\delta) \cdot \cos(83\overset{\circ}{.}52) \cdot \cos(75\overset{\circ}{.}49) \cdot \sin(37\overset{\circ}{.}77 - 40\overset{\circ}{.}66)\\ \sin(\gamma_5) =& + \cos(\delta) \cdot \big[\cos(83\overset{\circ}{.}52) \cdot \sin(40\overset{\circ}{.}66 - \alpha) \cdot \sin(75\overset{\circ}{.}49) \\ &+ \sin(\alpha - 318\overset{\circ}{.}56) \cdot \cos(75\overset{\circ}{.}49) \cdot \sin(83\overset{\circ}{.}52)\big] \\ & + \sin(\delta) \cdot \cos(83\overset{\circ}{.}52) \cdot \cos(75\overset{\circ}{.}49) \cdot \sin(318\overset{\circ}{.}56 - 40\overset{\circ}{.}66) \end{align}\tag{18}\]
Uranus
Das Postulat ist die Kreisförmigkeit der Mondbahnen und das die Monde in der Ringebene des Uranus liegen. Die Epoche ist 2000 Januar 1.5 und das Äquinoktium ist $J2000.0$.
$$\color{#cc0000}{d = JDE − 2451545.0}\tag{19}$$
| Tabelle 6 | ||
|---|---|---|
| Mond: | Radius: | mittlere Länge: |
| Ariel: | $r_1 = 7.470$ | $l_1 = 203\overset{\circ}{.}08553309448 + 142\overset{\circ}{.}8356475830\cdot (d - \tau) + \varphi - C$ |
| Umbriel: | $r_2 = 10.407$ | $l_2 = 251\overset{\circ}{.}20712282177 + 86\overset{\circ}{.}8688659668\cdot (d - \tau) + \varphi - C$ |
| Titania: | $r_3 = 17.070$ | $l_3 = 281\overset{\circ}{.}54711908352 + 41\overset{\circ}{.}3514099121\cdot (d - \tau) + \varphi - C$ |
| Oberon: | $r_4 = 22.828$ | $l_4 = 352\overset{\circ}{.}56292444211 + 26\overset{\circ}{.}7394809723\cdot (d - \tau) + \varphi - C$ |
Neptun
Die Bahn von Triton wird als kreisförmig angenommen. Die Epoche ist 1950 Januar 1.0 und das Äquinoktium ist $J1950.0$.
$$\color{#cc0000}{d = JD − 2433282.5}\tag{20}$$
| Tabelle 7 | ||
|---|---|---|
| Mond: | Radius: | mittlere Länge: |
| Triton: | $r = 14.3196575674$ | \(\begin{align} l &= 49\overset{\circ}{.}85334766\\ &+ 61\overset{\circ}{.}25726751\cdot (d - \tau)\\ &+ \varphi - C \end{align}\) |
Bahnneigung Tritons (retrograde Bewegung): $\gamma = 157\overset{\circ}{.}6852321$
Legende
$C$ = Mittelpunktsgleichung (Mpgl.) des Hauptplaneten (siehe Abschnitt Mittelpunktsgleichung)
$\varphi$ = Phasenwinkel des Hauptplaneten (siehe Abschnitt Phasenwinkel)
$r$ = Bahnradien der Monde in Planetenradien
$l$ = mittlere Länge der Monde mit Bezug auf die Sichtlinie Planet - Erde
$l'$ = korrigierte Länge der Monde mit Bezug auf die Sichtlinie Planet - Erde
$\tau$ = Lichtlaufzeit (siehe Abschnitt über die Lichlaufzeit)
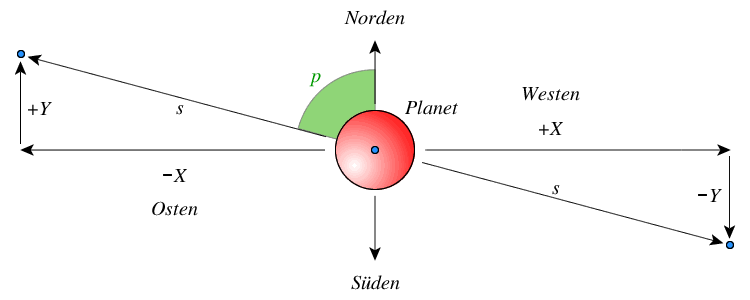
Darstellung der Monde am Himmel
Man berechne für alle Planetenmonde
\[\begin{align} X_k &= + r_k \cdot \sin(l_k)\\ &= s \cdot \cos(p - 90^{\circ}) \\ Y_k &= - r_k \cdot \cos(l_k) \cdot \sin(D_E)\\ &= s \cdot \sin(p - 90^{\circ}) \end{align}\tag{21}\]
und zusätzlich für Titan (Saturn II), Japetus und Triton:
\[\begin{align} X_j &= X_k \cdot \cos(\gamma) + Y_k \cdot \sin(\gamma)\\ &= s \cdot \cos(p - 90^{\circ}) \\ Y_j &= Y_k \cdot \cos(\gamma) - X_k \cdot \sin(\gamma)\\ &= s \cdot \sin(p - 90^{\circ}) \end{align}\tag{22}\]
Den Abstand $s$ und den Positionswinkel $p - 90^{\circ}$ erhält man im Abschnitt über die sphärische Darstellung.
$D_E$ = planetozentrische Deklination der Erde über der Äquatorebene des Planeten.
Helligkeit
Die absolute Helligkeit der natürlichen Satelliten aus $1\,AE$ Entfernung sind in der nachstehenden Tabelle angegeben.
| Tabelle 8 | ||
|---|---|---|
| Planet: | Name: | Magnitude: |
| Jupiter: | Io: | $m_1 = - 1\overset{m}{.}68 + 4\overset{m}{.}60 \ (\frac{\varphi}{100^{\circ}}) - 10\overset{m}{.}0 \ (\frac{\varphi}{100^{\circ}})^2$ |
| Europa: | $m_2 = - 1\overset{m}{.}41 + 3\overset{m}{.}12 \ (\frac{\varphi}{100^{\circ}}) - 12\overset{m}{.}5 \ (\frac{\varphi}{100^{\circ}})^2$ | |
| Ganymed: | $m_3 = - 2\overset{m}{.}09 + 3\overset{m}{.}23 \ (\frac{\varphi}{100^{\circ}}) - 6\overset{m}{.}6 \ (\frac{\varphi}{100^{\circ}})^2$ | |
| Kallisto: | $m_4 = - 1\overset{m}{.}05 - 7\overset{m}{.}80 \ (\frac{\varphi}{100^{\circ}}) - 27\overset{m}{.}4 \ (\frac{\varphi}{100^{\circ}})^2$ | |
| Saturn: | Tethys: | $m_1 = + 0\overset{m}{.}60 + 2\overset{m}{.}00 \ (\frac{\varphi}{100^{\circ}})$ |
| Dione: | $m_2 = + 0\overset{m}{.}80 + 2\overset{m}{.}29 \ (\frac{\varphi}{100^{\circ}})$ | |
| Rhea: | $m_3 = + 0\overset{m}{.}10 + 2\overset{m}{.}40 \ (\frac{\varphi}{100^{\circ}})$ | |
| Titan: | $m_4 = - 1\overset{m}{.}28 + 0\overset{m}{.}92 \ (\frac{\varphi}{100^{\circ}}) - 5\overset{m}{.}0 \ (\frac{\varphi}{100^{\circ}})^2$ | |
| Japetus: | $m_5 = + 1\overset{m}{.}48 - 2\overset{m}{.}5 \ \log_{10}(\color{#ff00ff}{H})$ | |
| Uranus: | Ariel: | $m_1 = + 1\overset{m}{.}45$ |
| Umbriel: | $m_2 = + 2\overset{m}{.}10$ | |
| Titania: | $m_3 = + 1\overset{m}{.}02$ | |
| Oberon: | $m_4 = + 1\overset{m}{.}23$ | |
| Neptun: | Triton: | $m_5 = - 1\overset{m}{.}24$ |
mit $$\color{#ff00ff}{H} = 0\overset{m}{.}571 - 0\overset{m}{.}429 \cdot \cos(V) \cdot \cos(l_5 - U)\tag{23}$$
Die scheinbare Helligkeit der Planetenmonde berechnet sich mit der Formel aus dem Abschnitt über die Helligkeit der Planeten. Die Gleichungen stammen aus dem Explanatory Supplement.
- Die Phasenwinkelabhängigkeit der Jupitermonde stammen von C. Blanco & S. Catalano und aus dem Explanatory Supplement.
- Weil Japetus eine gebundene Rotation hat und eine unterschiedliche Oberfläche mit verschiedenen Albedos aufweist, ist er in seiner westlichen Elongation um die zwei Magnituden heller als in der östlichen. Die Magnituden schwanken deshalb zwischen $10\overset{m}{.}1$ und $12\overset{m}{.}9$. Die Gleichung für $H$ stammt von D.L. Harris und D. Morrison.
- Die Phasenwinkelabhängigkeit Titans stammt von C. Blanco & S. Catalano.
- Die Phasenkoeffizienten für Tethys und Dione stammen von D. Morrison & D.P. Cruikshank, L.K. Kristensen und von C. Blanco & S. Catalano.
- Für Rhea wurde der Phasenkoeffizient von B.J. Buratti, J.A. Mosher et al. entnommen.
- Für Uranus und Neptun sind keine Phasenterme bekannt.