Inhaltsverzeichnis
Einfache Bahnbestimmung von Planetoiden
Einleitung
Hier wird in der Ephemeridenrechnung der umgekehrte Weg beschritten: Statt die Positionen der Himmelskörper vorherzusagen, werden aus den (mindestens drei) Beobachtungsergebnissen die bis dato unbekannten Bahnen der beobachteten Himmelsobjekte berechnet. Hier wird der Schwerpunkt auf das Gaußverfahren für Ellipsen (Planetoiden) und das Olbersverfahren für Parabeln (Kometen) gelegt. Um den Sachverhalt möglichst einfach zu illustrieren, wird auf das Buch von Wolfgang Wepner zurückgegriffen.
Ellipsen
Man hat drei Beobachtungszeitpunkte $t_1$ < $t_2$ < $t_3$ im Kalenderdatum oder besser im Julianischen Tagen mit den topozentrischen Koordinaten ($\alpha_1$, $\delta_1$, $t_1$), ($\alpha_2$, $\delta_2$, $t_2$) und ($\alpha_3$, $\delta_3$, $t_3$) und die rechtwinkeligen Sonnenkoordinaten $X_i$, $Y_i$, $Z_i$ (in die noch die zusätzlich erforderliche Ekliptikschiefe $\varepsilon$ miteinfließt) zu den ebenfalls drei Beobachtungszeitpunkten i = 1, 2, 3 zwischen 5 und 50 Tagen. Alle sechs Koordinaten habe das mittlere Äquinoktium des Datums und müssen in der Aberration korrigiert werden. Es gilt $$\vec{D}_i = \left(\begin{align} X_i \\ Y_i \\ Z_i \end{align}\right)\tag{1}$$ Der Abstand der Sonne R ergibt sich mit dem Absolutbetrag der rechtwinkeligen Koordinaten für jeden Zeitpunkt $t_i$: $$|\vec{D}_i| = R_i = \sqrt{X_i^2+Y_i^2+Z_i^2}\tag{2}$$
Die Zwischenzeiten $\tau_i$ lauten: \[\begin{aligned} \tau_1 &= k \cdot (t_3 - t_2)\\ \tau_2 &= k \cdot (t_3 - t_1)\\ \tau_3 &= k \cdot (t_2 - t_1) \end{aligned}\tag{3}\]
k ist die Gaußsche Gravitationskonstante. Die topozentrischen Koordinaten werden ebenfalls zu karthesischen Koordinaten $a_i$, $b_i$ und $c_i$ transformiert. \[\vec{d}_i = \left(\begin{aligned} & a_i \\ & b_i \\ & c_i \end{aligned}\right) = \left(\begin{aligned} & \cos(\delta_i)\cdot\cos(\alpha_i) \\ & \cos(\delta_i)\cdot\sin(\alpha_i) \\ & \sin(\delta_i) \end{aligned}\right)\tag{3}\]
Für jeden Zeitpunkt i werden die Skalarprodukte berechnet $$R_{ij} = \vec{d}_i\cdot\vec{D}_j\tag{4}$$
oder ausgeschrieben: \[\begin{aligned} R_{11} &= a_1\cdot X_1 + b_1\cdot Y_1 + c_1\cdot Z_1 \\ R_{21} &= a_2\cdot X_1 + b_2\cdot Y_1 + c_2\cdot Z_1 \\ R_{31} &= a_3\cdot X_1 + b_3\cdot Y_1 + c_3\cdot Z_1 \\ R_{12} &= a_1\cdot X_2 + b_1\cdot Y_2 + c_1\cdot Z_2 \\ R_{22} &= a_2\cdot X_2 + b_2\cdot Y_2 + c_2\cdot Z_2 \\ R_{32} &= a_3\cdot X_2 + b_3\cdot Y_2 + c_3\cdot Z_2 \\ R_{13} &= a_1\cdot X_3 + b_1\cdot Y_3 + c_1\cdot Z_3 \\ R_{23} &= a_2\cdot X_3 + b_2\cdot Y_3 + c_2\cdot Z_3 \\ R_{33} &= a_3\cdot X_3 + b_3\cdot Y_3 + c_3\cdot Z_3 \end{aligned}\tag{5}\]
Es ist in diesem Artikel zwischen einem Skalarprodukt $\vec{a}\cdot\vec{b}$ und einer Multiplikation a $\cdot$ b zu unterscheiden.
Weitere Hilfswerte sind:
$$H = \vec{D}_1\cdot\vec{D}_3 = X_1\cdot X_3 + Y_1\cdot Y_3 + Z_1\cdot Z_3\tag{6}$$
\[\begin{aligned} g_{12} &= \vec{d}_1\cdot\vec{d}_2 = a_1\cdot a_2 + b_1\cdot b_2 + c_1\cdot c_2 \\ g_{13} &= \vec{d}_1\cdot\vec{d}_3 = a_1\cdot a_3 + b_1\cdot b_3 + c_1\cdot c_3 \\ g_{23} &= \vec{d}_2\cdot\vec{d}_3 = a_2\cdot a_3 + b_2\cdot b_3 + c_2\cdot c_3 \end{aligned}\tag{7}\]
\[\begin{aligned} A_1 &= b_2\cdot c_3 - b_3\cdot c_2 \\ B_1 &= a_3\cdot c_2 - a_2\cdot c_3 \\ C_1 &= a_2\cdot b_3 - a_3\cdot b_2 \\ A_2 &= b_3\cdot c_1 - b_1\cdot c_3 \\ B_2 &= a_3\cdot c_1 - a_1\cdot c_3 \\ C_2 &= a_3\cdot b_1 - a_1\cdot b_3 \\ A_3 &= b_1\cdot c_2 - b_2\cdot c_1 \\ B_3 &= a_1\cdot c_2 - a_2\cdot c_1 \\ C_3 &= a_1\cdot b_2 - a_2\cdot b_1 \end{aligned}\tag{8}\]
oder zusammengefasst zu Vektorprodukten: $$\vec{A} = \left(\begin{aligned} A_1 \\ A_2 \\ A_3 \end{aligned}\right) = \vec{b} \times \vec{c}\tag{9}$$ $$\vec{B} = \left(\begin{aligned} B_1 \\ B_2 \\ B_3 \end{aligned}\right) = \vec{a} \times \vec{c}\tag{10}$$ $$\vec{C} = \left(\begin{aligned} C_1 \\ C_2 \\ C_3 \end{aligned}\right) = \vec{a} \times \vec{b}\tag{11}$$
Weitere Hilfsvariablen werden noch benötigt, bis mit der Iteration die Bahnbestimmung erfolgt. $$D=a_1\cdot A_1 + b_1\cdot B_1 + c_1\cdot C_1 = a_3\cdot A_3 + b_3\cdot B_3 + c_3\cdot C_3$$ Die nachfolgenden Werte müssen laut W. Wepner mit hoher Nachkommastellenzahl berechnet werden: \[\begin{aligned} d_{11} &= A_1\cdot X_1 + B_1\cdot Y_1 + C_1\cdot Z_1\\ d_{12} &= A_1\cdot X_2 + B_1\cdot Y_2 + C_1\cdot Z_2\\ d_{13} &= A_1\cdot X_3 + B_1\cdot Y_3 + C_1\cdot Z_3\\ d_{31} &= A_3\cdot X_1 + B_3\cdot Y_1 + C_3\cdot Z_1\\ d_{32} &= A_3\cdot X_2 + B_3\cdot Y_2 + C_3\cdot Z_2\\ d_{33} &= A_3\cdot X_3 + B_3\cdot Y_3 + C_3\cdot Z_3 \end{aligned}\tag{12}\]
Iteration
Die Iteration ist aufgrund des Sektor zu Dreieck Verhältnisses notwendig. Diese Diskrepanz wird mit diesem mathematischen Verfahren aufgehoben.
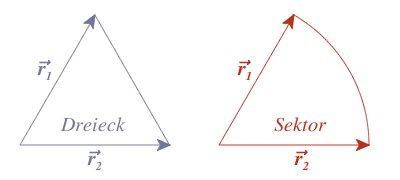 Abb. 1: Dreicks- und Sektorendarstellung der Bahnpositionen
Abb. 1: Dreicks- und Sektorendarstellung der Bahnpositionen
Der Quotient $\Psi = \frac{\text{Sektor}}{\text{Dreieck}}$ muß in der Iteration angepasst werden. Als Startwerte werden die nachfolgenden Ausdrücke genommen: $$w_1 = \frac{\tau_1}{\tau_2} \qquad w_3 = \frac{\tau_3}{\tau_2} \qquad\text{mit}\qquad w_1 + w_3 = 1\tag{13}$$
1.) Hier beginnt die äußere Iterationsschleife.
Nun werden die helio- und geozentrischen Abstände $r_i$ bzw. $\Delta_i$ zu den Zeitpunkten i = 1 und i = 3 berechnet: \[\begin{aligned} \Delta_1 &= \frac{w_1\cdot d_{11} + w_3\cdot d_{13} - d_{12}}{w_1 D} \\ \Delta_3 &= \frac{w_1\cdot d_{31} + w_3\cdot d_{33} - d_{32}}{w_3 D} \\ \rho_1 &= \Delta_1\cdot g_{12} - R_{12} \\ \rho_3 &= \Delta_3\cdot g_{23} - R_{23} \\ \Delta_2 &= w_1\cdot \rho_1 + w_3\cdot \rho_3 + R_{22} \\ r_1 &= \sqrt{\Delta_1^2 - 2\cdot\Delta_1\cdot R_{11} + R_1^2} \\ r_2 &= \sqrt{\Delta_2^2 - 2\cdot\Delta_2\cdot R_{22} + R_2^2} \\ r_3 &= \sqrt{\Delta_3^2 - 2\cdot\Delta_3\cdot R_{33} + R_3^2} \end{aligned}\tag{14}\]
Ergänzend zum Hilfswert H kommt noch $H^{\dagger}$ hinzu: $$H^{\dagger} = g_{13}\cdot\Delta_1\cdot\Delta_3 - \Delta_1\cdot R_{13} - \Delta_3\cdot R_{31} + H\tag{15}$$
mit $$r_2 = \sqrt{w_1^2\cdot r_1^2 + w_3^2\cdot r_3^2 + 2\cdot w_1\cdot w_3\cdot H^{\dagger}}\tag{16}$$
Als nächstes müssen alle drei Beobachtungszeitpunkte in der Lichtlaufzeit korrigiert werden: \[\begin{aligned} t_1' &= t_1 - 0.00577\cdot \Delta_1 \\ t_2' &= t_2 - 0.00577\cdot \Delta_2 \\ t_3' &= t_3 - 0.00577\cdot \Delta_3 \\ \tau_1' &= k \cdot (t_3' - t_2') \\ \tau_2' &= k \cdot (t_3' - t_1') \\ \tau_3' &= k \cdot (t_2' - t_1') \end{aligned}\tag{17}\]
mit $\tau_2' = \tau_1' + \tau_3'$. W. Wepner nennt die Lichtlaufzeit die planetare Aberration. Das Verfahren setzt sich in einer ziemlichen Rechengymnastik mit den Hansenkoeffizienten $h_1$ und $h_2$ fort: \[\begin{aligned} \varkappa_1 &= \sqrt{r_2\cdot r_3 + w_3\cdot r_3^2 + w_1\cdot H^{\dagger}} \\ \varkappa_2 &= \sqrt{r_1\cdot r_3 + H^{\dagger}} \\ \varkappa_3 &= \sqrt{r_1\cdot r_2 + w_1\cdot r_1^2 + w_3\cdot H^{\dagger}} \end{aligned}\tag{18}\] mit $$\sqrt{2}\cdot\varkappa_1\cdot\varkappa_3 = \varkappa_2\cdot (w_1\cdot r_1 + w_3\cdot r_3 + r_2)\tag{19}$$
Die Hansenkoeffizienten lauten: \[\begin{aligned} h_1 &= \frac{\tau_1'^2}{\varkappa_1^2\cdot (\chi\cdot\varkappa_1 + r_2 + r_3)} \\ h_3 &= \frac{\tau_3'^2}{\varkappa_3^2\cdot (\chi\cdot\varkappa_3 + r_1 + r_2)} \end{aligned}\qquad\text{mit}\qquad \chi = \frac{2\sqrt{2}}{3}\tag{20}\]
Das Verhältnis $\Psi$ von Sektor zu Dreieck wird durch folgende Gleichung für die Zeitpunkte i = 1 und i = 3 bestimmt:
Falls $h_i$ < 0.01, dann gilt: $$\Psi_i = 1 + \frac{5}{11}\cdot\left(\sqrt{1 + \frac{44}{9}\cdot h_i} - 1\right)\tag{21}$$
Falls $h_i$ > 0.01, dann gilt $u_0$ = $h_i$:
2.) Hier beginnt die innere Iterationsschleife.
$$u_{k+1} = u_k - \frac{u_k^3 + 2\cdot u_k^2 + (1 - h_i)\cdot u_k - \frac{10}{9}\cdot h_i}{3\cdot u_k^2 + 4\cdot u_k + (1 - h_i)}\tag{22}$$
Es handelt sich hier um das Newton - Raphson Verfahren. Die Iteration ist abzubrechen, wenn $|u_{k+1} - u_k| < 10^{-7}$ gilt. Dann ist $$\Psi_i = 1 + u_{k+1}\tag{23}$$
zu setzen.
3.) Hier endet die innere Iterationsschleife.
\[\begin{align} N_1 &= 1 + \frac{\sqrt{2}\cdot\tau_1'\cdot\tau_3'}{\Psi_1\cdot\Psi_3\cdot\varkappa_1\cdot\varkappa_2\cdot\varkappa_3} \\ N_2 &= \tau_1'\cdot\Psi_3 + \tau_3'\cdot\Psi_1 \\ w_1 &= \tau_1'\cdot\Psi_3\cdot\frac{N_1}{N_2} \\ w_3 &= \tau_3'\cdot\Psi_1\cdot\frac{N_1}{N_2}\end{align}\tag{24}\]
Nun hat man verbesserte Werte von $w_1$ und $w_3$. Die werden im Rücksprung zu 1.) oben wieder eingesetzt und die Iteration der äußeren Schleife solange wiederholt, bis sich $\Delta_i$ und $r_i$ nicht mehr ändern.
4.) Hier endet die äußere Iterationsschleife.
Bahnelemente
Die rechtwinkeligen Koordinaten des Himmelskörpers lauten: \[\begin{aligned} x_1 &= a_1\cdot\Delta_1 - X_1 \\ y_1 &= b_1\cdot\Delta_1 - Y_1 \\ z_1 &= c_1\cdot\Delta_1 - Z_1 \\ x_3 &= a_3\cdot\Delta_3 - X_3 \\ y_3 &= b_3\cdot\Delta_3 - Y_3 \\ z_3 &= c_3\cdot\Delta_3 - Z_3 \end{aligned}\tag{25}\]
Es gilt $H^{\dagger} = H^*$ mit $$H^* = x_1\cdot x_3 + y_1\cdot y_3 + z_1\cdot z_3\tag{26}$$
und \[\begin{aligned} a_2^{\dagger} &= \frac{w_1\cdot x_1 + w_3\cdot x_3 + X_2}{\Delta_2} \\ b_2^{\dagger} &= \frac{w_1\cdot y_1 + w_3\cdot y_3 + Y_2}{\Delta_2} \\ c_2^{\dagger} &= \frac{w_1\cdot z_1 + w_3\cdot z_3 + Z_2}{\Delta_2} \end{aligned}\tag{27}\]
mit $a_2 = a_2^{\dagger}$, $b_2 = b_2^{\dagger}$, $c_2 = c_2^{\dagger}$ als Bedingung. Hiermit ist die Überprüfung des zweiten Zeitpunkts i = 2 abgeschlossen. $$G = \frac{H^*}{x_1^2+y_1^2+z_1^2} = \frac{H^*}{r_1}\tag{28}$$ \[\begin{aligned} x_0 &= x_3 - G\cdot x_1 \\ y_0 &= y_3 - G\cdot y_1 \\ z_0 &= z_3 - G\cdot z_1 \end{aligned}\tag{29}\]
$$r_0 = \sqrt{x_0^2 + y_0^2 + z_0^2}\tag{30}$$ \[\begin{aligned} \sin(\nu_1 - \nu_3) &= \frac{r_0}{r_3} \\ \cos(\nu_1 - \nu_3) &= \frac{H^*}{r_1\cdot r_3} \end{aligned}\tag{31}\]
$$p = r_1^2\cdot r_0^2\cdot w_1\cdot w_3\cdot\frac{\Psi_1\cdot\Psi_3}{\tau_1'\cdot\tau_3'}\tag{32}$$ \[\begin{aligned} q_1 &= \frac{p}{r_1} - 1 \\ q_3 &= \frac{p}{r_3} - 1 \end{aligned}\tag{33}\]
\[\begin{aligned} \epsilon\cdot\sin(\nu_1) &= q_1\frac{\cos(\nu_1 - \nu_3) - q_3}{\sin(\nu_1 - \nu_3)} = s_1 \\ \epsilon\cdot\cos(\nu_1) &= q_1 \end{aligned}\tag{34}\]
Die Bahnformelemente a und $\epsilon$ sind: \[\begin{array}{cl} \epsilon = \sqrt{s_1^2 + q_1^2} & \text{numerische Exzentrizität} \\ a = \dfrac{p}{1 - \epsilon^2} & \text{große Halbachse} \end{array}\tag{35}\]
Für die Zeitpunkte i = 1 und i = 3 sind die Bahnpositionselemente $\nu_i$, $E_i$, $M_i$, T und n zu berechnen: \[\begin{array}{cl} \nu_1 = \arctan\left(\dfrac{s_1}{q_1}\right) & \text{wahre Anomalie zum Zeitpunkt i=1} \\ \nu_3 = \nu_1 - \arctan\left(\dfrac{r_0\cdot r_1}{H^*}\right) & \text{wahre Anomalie zum Zeitpunkt i=3} \\ \tan\left(\dfrac{E_i}{2}\right) = \sqrt{\dfrac{1 - \epsilon}{1 + \epsilon}}\cdot \tan\left(\dfrac{\nu_i}{2}\right) & \text{exzentrische Anomalie} \\ M_i = E_i - \dfrac{180^{\circ}}{\pi}\cdot\epsilon\cdot\sin(E_i) & \text{mittlere Anomalie} \\ n = \dfrac{M_3 - M_1}{t_3' - t_1'} & \text{mittlere tägliche Bewegung} \\ T = t_1' - \dfrac{M_1}{n} = t_3' - \dfrac{M_3}{n} & \text{Perihelzeit} \end{array}\tag{36}\]
Bei $\nu_1$ und $\nu_3$ ist auf die quadrantenrichtige Darstellung zu achten. Es folgen nun die Bahnlageelemente i, $\Omega$, $\omega$ und $\varpi$. Hierzu werden die Gaußvektoren $\vec{P}$, $\vec{Q}$ und $\vec{S}$ benötigt: \[\begin{aligned} P_1 &= \frac{x_1}{r_1}\cdot\cos(\nu_1) - \frac{x_0}{r_0}\cdot\sin(\nu_1) \\ P_2 &= \frac{y_1}{r_1}\cdot\cos(\nu_1) - \frac{y_0}{r_0}\cdot\sin(\nu_1) \\ P_3 &= \frac{z_1}{r_1}\cdot\cos(\nu_1) - \frac{z_0}{r_0}\cdot\sin(\nu_1) \\ Q_1 &= \frac{x_1}{r_1}\cdot\sin(\nu_1) + \frac{x_0}{r_0}\cdot\cos(\nu_1) \\ Q_2 &= \frac{y_1}{r_1}\cdot\sin(\nu_1) + \frac{y_0}{r_0}\cdot\cos(\nu_1) \\ Q_3 &= \frac{z_1}{r_1}\cdot\sin(\nu_1) + \frac{z_0}{r_0}\cdot\cos(\nu_1) \end{aligned}\tag{37}\]
Es gilt $|\vec{P}| = P_1^2 + P_2^2 + P_3^2$ = 1 und $|\vec{Q}| = Q_1^2 + Q_2^2 + Q_3^2$ = 1. Der letzte Vektor $\vec{S}$ steht senkrecht auf der Ebene und wird durch ein Kreuzprodukt ermittelt: $$\vec{S} = \vec{P} \times \vec{Q}\tag{38}$$
oder ausgeschrieben: \[\begin{aligned} S_1 &= P_2\cdot Q_3 - P_3\cdot Q_2 \\ S_2 &= P_3\cdot Q_1 - P_1\cdot Q_3 \\ S_3 &= P_1\cdot Q_2 - P_2\cdot Q_1 \end{aligned}\tag{39}\]
Es gelten die Skalarprodukte $\vec{S}\cdot\vec{P}$ = 0 und $\vec{S}\cdot\vec{Q}$ = 0. Jetzt werden final die Bahnlageelemente berechnet: \[\begin{aligned} F_1 = \cos(i) &= - S_2\cdot\sin(\epsilon) + S_3\cdot\cos(\epsilon) \\ F_2 = \sin(\Omega) &= + \frac{S_1}{\sin(i)} \\ F_3 = \cos(\Omega) &= - \frac{S_2\cdot\cos(\epsilon) + S_3\cdot\sin(\epsilon)}{\sin(i)} \\ F_4 = \sin(\omega) &= - Q_1\cdot F_3 - (Q_2\cdot\cos(\epsilon) + Q_3\cdot\sin(\epsilon))\cdot F_2 \\ F_5 = \cos(\omega) &= + P_1\cdot F_3 + (P_2\cdot\cos(\epsilon) + P_3\cdot\sin(\epsilon))\cdot F_2 \end{aligned}\tag{40}\]
\[\begin{array}{cl} i = \arccos(F_1) & \text{Bahnneigung} \\ \Omega = \arctan\left(\dfrac{F_2}{F_3}\right) & \text{Bahnknoten} \\ \omega = \arctan\left(\dfrac{F_4}{F_5}\right) & \text{Argument des Perihels} \\ \varpi = \omega + \Omega & \text{Perihellänge} \end{array}\tag{41}\]
Bei $\Omega$ und $\omega$ ist wieder auf die quadrantenrichtige Darstellung zu achten.
Beispiel (gekürzte Fassung)
Es soll die Bahn von 1069 Planckia anhand von drei Beobachtungen bestimmt werden. Das Äquinoktium der topozentrisch - äquatorialen Koordinaten $\alpha$ und $\delta$ ist der B1950.0
| Nr. | Zeitpunkt | $\alpha$ | $\delta$ |
|---|---|---|---|
| 1 | 18.04.1978 um $22^h 11^m 0\overset{s}{.}384$ | $15^h 9^m 18\overset{s}{.}24$ | $02^{\circ} 43' 36\overset{"}{.}1$ |
| 2 | 04.05.1978 um $23^h 04^m 8\overset{s}{.}544$ | $14^h 58^m 9\overset{s}{.}36$ | $04^{\circ} 05' 30\overset{"}{.}1$ |
| 3 | 01.06.1978 um $22^h 52^m 33\overset{s}{.}88$ | $14^h 39^m 52\overset{s}{.}27$ | $04^{\circ} 38' 13\overset{s}{.}6$ |
Die zum Datum korrespondierenden, rechtwinkeligen Sonnenkoordinaten $X_i$, $Y_i$ und $Z_i$ erhält man aus dem Internet (früher aus dem Astronomical Almanac). Diese müssen noch ins topozentrische Koordinatensystem konvertiert und in Grad umgerechnet werden. Die Zeitpunkte $t_i$ werden auf den 0.4.1978 bezogen.
| i | $t_i[^d]$ | $\alpha[^{\circ}]$ | $\delta[^{\circ}]$ | $X_i$ | $Y_i$ | $Z_i$ |
|---|---|---|---|---|---|---|
| 1 | 18.92431 | 227.326000 | 2.727528 | 0.8858062 | 0.4342838 | 0.1882691 |
| 2 | 34.96131 | 224.539000 | 4.091694 | 0.7289568 | 0.6395160 | 0.2772560 |
| 3 | 62.95317 | 219.967792 | 4.637111 | 0.3356087 | 0.8780688 | 0.3806934 |
Die Schiefe der Ekliptik $\varepsilon$ wird als erste ermittelt: $$\varepsilon = 23\overset{\circ}{.}44579$$
Der Abstand der Sonne $R_i$ lautet: $$R_1 = 1.004340728\qquad R_2 = 1.008578019\qquad R_3 = 1.014182174$$
Es folgen die karthesischen Koordinaten $a_i$, $b_i$ und $c_i$: \[\begin{array}{lll} a_1 = -0.677058216 & a_2 = -0.710956429 & a_3 = -0.763896999 \\ b_1 = -0.734389345 & b_2 = -0.699606838 & b_3 = -0.640254276 \\ c_1 = +0.047586366 & c_2 = +0.071352848 & c_3 = +0.080844530 \end{array}\]
Die korrespondierenden Zwischenzeiten $\tau_1$, $\tau_2$ und $\tau_3$ berechnen sich zu: $$\tau_1 = 0.481518746\qquad\tau_2 = 0.757388806\qquad\tau_3 = 0.275870061$$
Nachdem man die Hilfsvariablen H, $R_{ij}$, $g_{ij}$, $\vec{A}$, $\vec{B}$, $\vec{C}$, D und $d_{ij}$ durchgerechnet hat, ergibt sich für $w_1$ und $w_3$: $$w_1 = 0.635761636\qquad w_3=0.364238366$$
Nun startet die Iteration mit 6 Durchläufen. Zu berechnen zu jedem Zeitpunkt i sind: $\Delta_i$, $r_i$, H$^{\dagger}$, $\kappa_i$, $h_i$ und $\Psi_i$. Bei der ersten und zweiten Iteration muß die oben erwähnte Aberrationkorrektur mit berücksichtigt werden:
1. Iteration: \[\begin{array}{ll} \tau_1' = 0.481504772 & \tau_3' = 0.275872134 \\ w_1 = 0.637092118 & w_2 = 0.365357523 \end{array}\]
2. Iteration: \[\begin{array}{ll} \tau_1' = 0.481505901 & \tau_3' = 0.275871645 \\ w_1 = 0.637201576 & w_2 = 0.365447051 \end{array}\]
5. Iteration: \[\begin{array}{ll} w_1 = 0.637211746 & w_2 = 0.365455539 \end{array}\]
6. Iteration:
| Es werden noch $\Delta_i$ und $r_i$ berechnet, dann sind die Differenzen klein genug, um die Iteration abzubrechen. |
Die rechtwinkeligen Koordinaten des Kleinplaneten sind: \[\begin{array}{ll} x_1 = -2.218456268 & x_3 = -1.925402428 \\ y_1 = -1.879778423 & y_3 = -2.210541939 \\ z_1 = -0.094605110 & z_3 = -0.212442802 \end{array}\]
mit $r_1$ = 2.909306663 und $r_3$ = 2.939183920. Die für dieBahnlageelemente wichtigen Gaußvektoren sind: \[\begin{array}{lll} P_1 = -0.987882080 & Q_1 = -0.060403098 & S_1 = +0.142970125 \\ P_2 = +0.028205763 & Q_2 = -0.975691908 & S_2 = +0.217324040 \\ P_3 = +0.152621839 & Q_3 = -0.210657944 & S_3 = +0.965572267 \end{array}\]
Jetzt werden nacheinander und in dieser Reihenfolge die Bahnelemente bestimmt: \[\begin{aligned} \nu_1 &= 43\overset{\circ}{.}10438568 \\ \nu_3 &= 52\overset{\circ}{.}05552009 \\ \epsilon &= 0.094304556 \\ a &= 3.137523365 AE \\ M_1 &= 36\overset{\circ}{.}08955082 \\ M_3 &= 43\overset{\circ}{.}89781710 \\ n &= 0\overset{\circ}{.}177346911 \\ T &= -184\overset{d}{.}5840094 \\ T &= 27.09.1977\text{ um } 9^h 59^m 2\overset{s}{.}4 \\ i &= 13\overset{\circ}{.}51204632 \\ \Omega &= 142\overset{\circ}{.}2730440 \\ \omega &= 33\overset{\circ}{.}45249370 \end{aligned}\]
Ein Vergleich mit den (damals) Leningrader Ephemeriden der Kleinplaneten liefert: \[\begin{aligned} a &= 3.1388031 AE \\ \epsilon &= 0.0949682 \\ n &= 0\overset{\circ}{.}17723846 \\ T &= 27.09.1977\text{ um } 13^h 29^m 16\overset{s}{.}8 \\ i &= 13\overset{\circ}{.}51219 \\ \Omega &= 142\overset{\circ}{.}27930 \\ \omega &= 33\overset{\circ}{.}42716 \end{aligned}\]
Die Berechnung der Bahnelemente und damit die Bahnbestimmung ist nun abgeschlossen. In der Regel muß die Bahnberechnung dann wiederholt werden, wenn mehr beobachtete Positionen mit i = 4, 5, 6, etc.. vorliegen.