Inhaltsverzeichnis
Die Zeitgleichung
Als Zeitgleichung ($ZGL$) bezeichnet man die Differenz von wahrer und mittlerer Ortszeit. Die mittlere Ortszeit ist jene, die wir auf einer Uhr ablesen. Eine Sonnenuhr hingegen zeigt die wahre Ortszeit.
Abb. 1: Die wahre Bewegung der Sonne verursacht ein Analemma
Wenn die mittlere Sonne den Meridian eines Beobachters durchläuft, ist dort mittlerer Mittag. Wahrer Mittag ist jener Moment, in dem die wahre Sonne den Meridian durchläuft. Die $ZGL$ ist die Differenz zwischen der wahren Ortszeit $WOZ$ und mittleren Ortszeit $MOZ$. Mit anderen Worten, die $ZGL$ ist die Differenz zwischen den Stundenwinkeln der wahren Sonne und der mittleren Sonne.
$$\large E = WOZ - MOZ$$
Im englischen Sprachraum wird oft der Buchstabe $E$ für „Equation of time“ verwendet. Aufgrund der Exzentrizität ihrer Umlaufbahn und in viel geringerem Maße aufgrund der Störungen durch den Mond und die Planeten variiert die heliozentrische Länge $L$ der Erde nicht gleichmäßig. Daraus folgt, dass die Sonne die Ekliptik mit einer ungleichförmigen Geschwindigkeit durchläuft. Aus diesem Grund und auch dadurch, dass sich die Sonne in der Ekliptik und nicht entlang des Himmelsäquators bewegt, nimmt die Rektaszension $\alpha_{\odot}$ der Sonne nicht gleichmäßig zu.
- Man stelle sich eine erste fiktive Sonne vor, die sich mit konstanter Geschwindigkeit entlang der Ekliptik bewegt und mit der wahren Sonne am Perihel und Aphel zusammenfällt (Sonnennähe bzw. Sonnenferne).
- Weiters betrachtet man eine zweite fiktive Sonne, die sich mit konstanter Geschwindigkeit den Himmelsäquator entlang bewegt und mit der ersten fiktiven Sonne zu den Tag-Nacht-Gleichen zusammenfällt. Diese zweite fiktive Sonne ist die mittlere Sonne, und ihre Rektaszension $\alpha_{\odot}$ nimmt definitionsgemäß gleichmäßig zu.
Definiert man also diese mittlere Sonne wie beschrieben, ergibt sich ein Zeitunterschied, der durch folgende Beziehung beschrieben werden kann:
$$ E = {L_0} - 0.0057183 - {\alpha _ \odot } + \Delta \psi \cdot \cos \varepsilon$$
In dieser Gleichung ist die Konstante $0.0057183^{\circ}$ die Summe aus dem Mittelwert der Aberration in Länge $-20\overset{''}{.}49552$ und der Korrektur zur Reduktion auf das FK5-System (Fundamental-Katalog), $-0\overset{''}{.}09033$. Im Rahmen der Genauigkeit, die hier besprochen wird, kann letztere Korrektur auch weggelassen werden.
$\alpha_{\odot}$ ist die scheinbare Rektaszension der Sonne, berechnet unter Berücksichtigung der Aberration und der Nutation. Die Größe $\Delta \psi \cdot \cos \varepsilon$, wobei $\Delta \psi$ die Nutation in Länge und $\varepsilon$ die wahre Schiefe der Ekliptik ist, wird benötigt, um die scheinbare Rektaszension der Sonne auf das Äquinoktium des Datums zu beziehen, ebenso wie die mittlere Länge $L_0$.
In der gegebenen Formel sollten die Größen $L_0, \alpha_{\odot}, \Delta\psi$ in Grad ausgedrückt werden. Damit wird auch die $ZGL$ in Grad ausgedrückt. Sie kann dann durch Multiplikation mit $4\frac{m}{\circ}$ in Minuten umgewandelt werden.
$$24^{h} \hat{=}\; 360^{\circ} \; \Rightarrow \; 1^{h} \hat{=}\; 15^{\circ} \; \Rightarrow \; 4^{m} \hat{=}\; 1^{\circ}$$
Die oben angegebene Vorgehensweise entspricht der exakten Berechnung der $ZGL$. Sie setzt jedoch genaue Berechnungen der Erdkoordinaten voraus, z.B. nach der VSOP87 oder einer anderen Planetentheorie, was schnell aufwändig werden kann. Auf dieser Seite wird daher ein einfacherer Algorithmus verwendet, der schneller ist, jedoch immer noch sehr gute Ergebnisse liefert.
Der Wert der $ZGL$ für den hier dargestellten Jahresbereich liegt immer innerhalb des Intervalls $\pm 20$ Minuten.
Berechnung der Zeitgleichung
Der hier verwendete Algorithmus zur Berechnung der $ZGL$ wird von J. Meeus in Astronomical Algorithms angeführt. Sie stammt aus dem Textbook on Spherical Astronomy von W.M. Smart. Dieser Algorithms verwendet zur Berechnung eine Reihenentwicklung für die mittlere Anomalie $M$ und die mittlere Länge $L_0$ der Sonne, sowie die Werte der Ekliptikschiefe $\varepsilon$ und der Exzentrizität $\epsilon$ der Erdbahn. Der Wert der $ZGL$ wird bei Smart mit $E$ bezeichnet und in Radiant ausgegeben.
Ein gegebenes Datum wird zunächst in julianische Tage $JD$ umgerechnet. Mit
$$T = \frac{JD - 2451545.0}{36525}$$
berechnet man dann folgende Grundgrößen:
| Exzentrizität der Erdbahn: | \( \begin{align} \epsilon &= 0.016708634 \\ &- 0.000042037 \cdot T\; \\ &- 0.0000001267 \cdot T^2 \end{align}\) |
| Mittlere Schiefe der Ekliptik: | \(\begin{align} \varepsilon_{0} &= 0.016708634\\ &- 0.000042037 \cdot T\\ &- 0.0000001267 \cdot T^2\\ \end{align}\) |
| Hilfsgröße $y$: | \(y = \tan^2\left( {\frac{\varepsilon_{0} }{2}} \right)\) |
| Mittlere Länge der Sonne: | \(\begin{align} {L_0} &= 280\overset{{\circ}}{.}46646\\ &+ 36000\overset{{\circ}}{.}76983 \cdot T\\ &+ 0\overset{{\circ}}{.}0003032 \cdot T^2 \end{align}\) |
| Mittlere Anomalie der Sonne: | \(\begin{align} M &= 357\overset{{\circ}}{.}52911\\ &+ 35999\overset{{\circ}}{.}05029 \cdot T\\ &- 0\overset{{\circ}}{.}0001537 \cdot T^2 \end{align}\) |
Damit ist die Zeitgleichung (in Radiant, Hempe & Molt) gegeben durch den Ausdruck mit $y = \tan^2(\frac{\varepsilon}{2})$
\[\begin{align} E^{rad} &= y \cdot \sin (2\cdot L_0) \\ &- 2 \cdot \epsilon \cdot \sin (M) \\ &+ 4 \cdot \epsilon \cdot y \cdot \sin (M) \cdot \cos (2\cdot L_0) \\ &- \frac{1}{2} \cdot y^2 \cdot \sin (4\cdot L_0) \\ &- \frac{5}{4} \cdot \epsilon^2 \cdot \sin (2\cdot M) \\ \end{align}\]
Die Winkelwerte für $\varepsilon, L_0, M$ werden hier in in Grad berechnet. Für die $ZGL$ achte man auf die Argumente innerhalb der Sinus- bzw. Cosinusfunktionen. Die meisten Programmiersprachen benötigen Bogenmaßwerte als Argumente der trigonometrischen Funktionen und müssen durch Multiplikation mit $\frac{\pi}{180}$ entsprechend konvertiert werden.
Die Umrechnung des Ergebnisses von $E$ in Grad erfolgt mittels Multiplikation mit $\tfrac{180}{\pi}$, danach wird mit $4$ multipliziert, um den Zeitwert in dezimalen Minuten zu erhalten. Dieser wird schließlich in Minuten und Sekunden umgewandelt, um die Ausgabe in $\pm\textrm{mm:ss}$ zu erhalten. Die Genauigkeit des hier vorgestellten Verfahrens liegt etwa bei $\pm 4^{s}$ für Daten im Zeitraum $-2000$ bis $+5000$.
Zeitgleichung von -2000 bis +5000
Die Kurve, die den Verlauf der $ZGL$ im Laufe eines Jahres darstellt ist bekannt und in vielen Astronomiebüchern zu finden (Abb.2). Gegenwärtig (2024) hat die Kurve ein tiefes Minimum nahe dem 11. Februar, ein hohes Maximum nahe dem 3. November und ein sekundäres Maximum und Minimum um den 14. Mai bzw. am 26. Juli. Der Verlauf der $ZGL$ ändert sich jedoch im Laufe der Jahrhunderte allmählich, weil sich die Schiefe der Ekliptik, die Exzentrizität und die Länge des Perihels der Erdbahn langsam ändern.
- Roter Bereich: Die Zeitgleichung ist negativ, die Sonnenuhr geht gegenüber der mittleren Sonne nach.
- Grüner Bereich: Die Zeitgleichung ist positiv, die Sonnenuhr eilt der mittleren Sonne voraus.
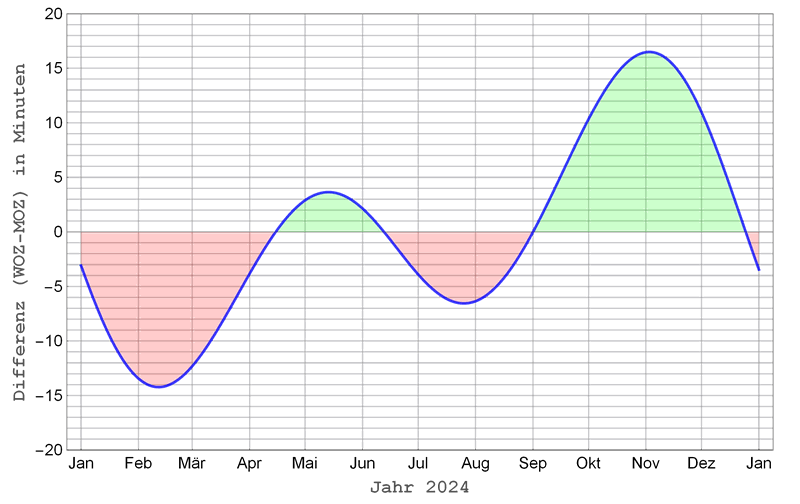Abb. 2: Zeitgleichung für das Jahr 2024
Die nachstehende Abb.3 zeigt den Verlauf der $ZGL$ von $-2000$ bis $+5000$. Auf der vertikalen Skala werden die Daten in Abständen von fünf Minuten angegeben. Man sieht zum Beispiel, dass das Minimum im Februar in ferner Zukunft weniger tief sein wird.
Abb. 3: Die Zeitgleichung im Laufe der Jahrtausende
Im Jahr 1246 n.Chr., als das Perihel der Erde mit der Wintersonnenwende zusammenfiel, war der Graph der $ZGL$ bezüglich der Null-Linie genau symmetrisch: Das Minimum des Februars war genau so tief wie das Maximum im November hoch war, und das kleinere Mai-Maximum war genau so hoch wie der tiefste Wert des Juli-Minimums.
Zwischen 1600 und 2100 n.Chr. variieren die Extremwerte der Zeitgleichung, wie in der unten stehenden Tabelle gezeigt wird. Dies sind mittlere Werte: Die Berechnung basiert auf einer ungestörten elliptischen Bewegung der Erde, und die Nutation wurde hier nicht berücksichtigt. Die Werte weichen daher von der exakten Berechnung etwas ab.
Tabelle: Haupt- und Nebenmaxima/minima
| Jahr | Februar-Minimum | Mai-Maximum | Juli-Minimum | November-Maximum |
|---|---|---|---|---|
| $1600$ | $-15^{m} 01^{s}$ | $+4^{m} 19^{s}$ | $-5^{m} 40^{s}$ | $+16^{m} 03^{s}$ |
| $1700$ | $-14^{m} 50^{s}$ | $+4^{m} 09^{s}$ | $-5^{m} 53^{s}$ | $+16^{m} 09^{s}$ |
| $1800$ | $-14^{m} 38^{s}$ | $+3^{m} 59^{s}$ | $-6^{m} 05^{s}$ | $+16^{m} 15^{s}$ |
| $1900$ | $-14^{m} 27^{s}$ | $+3^{m} 50^{s}$ | $-6^{m} 18^{s}$ | $+16^{m} 20^{s}$ |
| $2000$ | $-14^{m} 15^{s}$ | $+3^{m} 41^{s}$ | $-6^{m} 31^{s}$ | $+16^{m} 25^{s}$ |
| $2100$ | $-14^{m} 03^{s}$ | $+3^{m} 32^{s}$ | $-6^{m} 44^{s}$ | $+16^{m} 30^{s}$ |
| $1246$ | $-15^{m} 39^{s}$ | $+4^{m} 58^{s}$ | $-4^{m} 58^{s}$ | $+15^{m} 39^{s}$ |
Beispiel
Man berechne die Zeitgleichung für den 21.5.2023 um 10:15 $MESZ$.
Die Umrechnung der mitteleuropäischen Sommerzeit in Weltzeit $UT$ ergibt
$UT = MESZ - 2^{h} = \textrm{10:15} - 02^{h} = \textrm{08:15}$
Der julianische Tag für diesen Zeitpunkt wurde bereits in diesem Beispiel berechnet zu $JD = 2460085.84375$.
Damit erhält man
\(\begin{align} T &= \frac{2460085.84375 - 2451545.0}{36525}\\ &= 0.2338355578370979 \end{align}\)
Die Werte $\epsilon, \varepsilon_{0}, y, L_{0}, M$ ergeben sukzessive
\(\begin{align} \epsilon &= 0.016698797\\ \varepsilon_{0} &= 23\overset{\circ}{.}436250\\ y &= 0.043023\\ L_{0} &= 58\overset{\circ}{.}726572\\ M &= 135\overset{\circ}{.}387108 \end{align}\)
Für die Zeitgleichung des gegebenen Zeitpunkts erhält man damit
$E = 0\overset{rad}{.}014897883$
Die Umrechnung in Grad liefert
\(\begin{align} E &= 0\overset{rad}{.}014897883\cdot \frac{180}{\pi}\\ &= 0\overset{\circ}{.}853586 \end{align}\)
Die Umrechnung in Minuten durch Multiplikation mit $4\frac{m}{\circ}$ ergibt
$E = 3.414343$ Dezimalminuten.
Eine Umrechnung in das Format $\textrm{mm:ss}$ mithilfe der Funktionen trunc bzw. frac ergibt
\(\begin{align} m &= \textrm{trunc}(3\overset{m}{.}414343) = +3^m\\ s &= \textrm{frac}(3\overset{m}{.}414343)\cdot 60\tfrac{s}{m}\\ &= 0\overset{m}{.}414343\cdot 60\tfrac{s}{m} = 24\overset{s}{.}8606\approx 25^s \end{align}\)
Die Zeitgleichung am 21.5.2023 um 10:15 $MESZ$ beträgt also $+3^{m}25^{s}$. Der Wert ist positiv, daher eilt eine Sonnenuhr der mittleren Ortszeit um diesen Betrag voraus. Wahrer Mittag ist also um $3^{m}25^{s}$ früher als der Mittag nach mittlerer Ortszeit. Die Astronomiesoftware GUIDE liefert dasselbe Ergebnis.