Inhaltsverzeichnis
Wichtige mathematische Anwendungen
Hier werden die mathematischen Anwendungen beschrieben, die nicht als Funktionen in Taschenrechnern und Computerprogrammen zu finden sind. Diese Liste wird laufend ergänzt.
Lineare Gleichungssysteme
Hat man drei Gleichungen in der Form \[\begin{align} b_1 &= a_{11} \cdot x + a_{12} \cdot y + a_{13} \cdot z \\ b_2 &= a_{21} \cdot x + a_{22} \cdot y + a_{23} \cdot z \\ b_3 &= a_{31} \cdot x + a_{32} \cdot y + a_{33} \cdot z \end{align}\tag{1}\]
so kann man diese leicht als Matrix und Vektor darstellen: \[\left(\begin{matrix} b_1 \\ b_2 \\ b_3 \end{matrix}\right) = \left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right) \cdot \left(\begin{matrix} x \\ y \\ z \end{matrix}\right)\tag{2}\]
Die Multiplikation erfolgt mit der folgenden graphischen Rechenregel:
Vektoren
Aus den drei Gleichungen \[\begin{align} x &= r\cdot \cos(\beta)\cdot \cos(\alpha)\\ y &= r\cdot \cos(\beta)\cdot \sin(\alpha)\\ z &= r\cdot \sin(\beta)\end{align}\tag{3}\]
formt man den Vektor \[\vec{r} = r \left(\begin{matrix} \cos(\beta)\cdot \cos(\alpha)\\ \cos(\beta)\cdot \sin(\alpha)\\ \sin(\beta)\end{matrix}\right) = r\cdot \vec{e}\tag{4}\]
Betrag
Der Betrag eines Vektors ist seine Länge, also ein Skalar (= eine Zahl).
Der Betrag im 2-dimensionalen Raum ist:
$$\vert \vec{u} \vert = \sqrt{u_1^2 + u_2^2}\tag{5}$$
Der Betrag im 3-dimensionalen Raum ist:
$$\vert \vec{u} \vert = \sqrt{u_1^2 + u_2^2 + u_3^2}\tag{6}$$
Skalarprodukt (Punktprodukt)
$$\vec{v} \cdot \vec{u} = v_1 \cdot u_1 + v_2 \cdot u_2 + + v_3 \cdot u_3\tag{7}$$
Rechenregeln: $$\vec{v} \cdot \vec{u} = \vec{u} \cdot \vec{v}\tag{8}$$ $$\vec{u} \cdot \vec{u} = |u|^2\tag{9}$$ $$\vec{u} \cdot \vec{v} = |\vec{u}|\cdot|\vec{v}|\cdot \cos(\theta)\tag{10}$$
senkrecht $\theta = 90^\circ$: $$\vec{u} \cdot \vec{v} = 0\tag{11}$$
parallel $\theta = 0^\circ$: $$\vec{u} \cdot \vec{v} = |\vec{u}|\cdot|\vec{v}|\tag{12}$$
Vektorprodukt (Kreuzprodukt)
$$\vec{v} \times \vec{u} = \left(\begin{array} vv_2 \cdot u_3 - v_3 \cdot u_2 \\ v_3 \cdot u_1 - u_3 \cdot v_1 \\ v_1 \cdot u_2 - u_1 \cdot v_2 \end{array}\right)\tag{13}$$
Rechenregeln: $$\vec{v} \times \vec{u} = - \vec{u} \times \vec{v}\tag{14}$$ $$\vec{u} \times \vec{u} = 0\tag{15}$$ $$\vec{u} \times \vec{v} = |\vec{u}|\cdot|\vec{v}|\cdot \sin(\theta)\tag{16}$$
senkrecht $\theta = 90^\circ$: $$\vec{u} \times \vec{v} = |\vec{u}|\cdot|\vec{v}|\tag{17}$$
parallel $\theta = 0^\circ$: $$\vec{u} \times \vec{v} = 0\tag{18}$$
Matrizen
Drehmatrizen
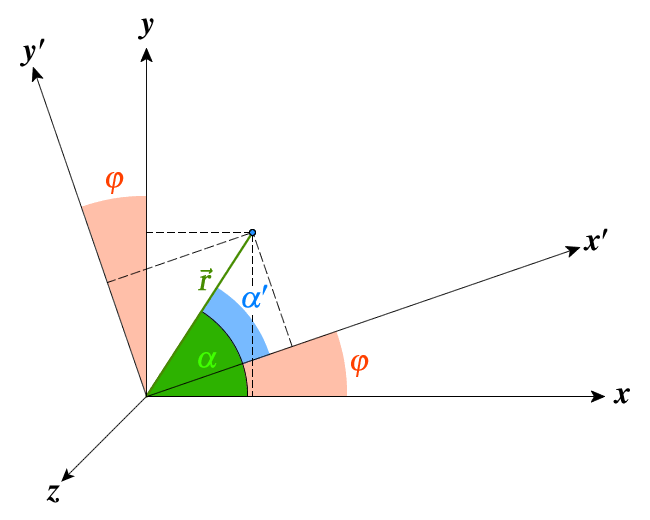
Ein Vektor wird mit Hilfe einer Drehmatrix in eine neues Koordinatensystem (i.e. neuer Vektor) gedreht (Abb. 1). \[\begin{split} & x = \cos(\alpha) \\ & y = \sin(\alpha) \\ & z = 0 \end{split} \Rightarrow\vec{r}(\alpha,0) = \left( \begin{matrix} x \\ y \\ z \end{matrix} \right) = \left( \begin{matrix} \cos(\alpha) \\ \sin(\alpha) \\ 0 \\ \end{matrix} \right) = \vec{e}(\alpha,0)\tag{19}\]
Nach einer Drehung mit dem Winkel $\varphi$ um die $z$-Achse erhält man:
\[\vec{r} = \left( \begin{matrix} x' \\ y' \\ z' \end{matrix} \right) = \left( \begin{matrix} \cos(\alpha') \\ \sin(\alpha') \\ z \end{matrix} \right) = \left( \begin{matrix} \cos(\alpha - \varphi) \\ \sin(\alpha - \varphi) \\ z \end{matrix} \right) = \left( \begin{array}{lll} + x \ \cos(\varphi) & + y \ \sin(\varphi) & + z \ 0 \\ - x \ \sin(\varphi) & + y \ \cos(\varphi) & + z \ 0 \\ + x \ 0 & + y \ 0 & + z \ 1 \end{array} \right)\tag{20}\]
\[\Rightarrow \vec{r}'(\alpha',0) = \left( \begin{matrix} x' \\ y' \\ z' \end{matrix} \right) = \left( \begin{array}{ccc} + \cos(\varphi) & + \sin(\varphi) & 0 \\ - \sin(\varphi) & + \cos(\varphi) & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{matrix} x \\ y \\ z \end{matrix} \right) = R_3(\varphi) \vec{r}(\alpha,0)\tag{21}\]
Die Drehungen um einen Winkel $\varphi$ um die $x$-Achse ($R_1$), $y$-Achse ($R_2$) und die $z$-Achse ($R_3$):
\[R_1(\varphi) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & + \cos(\varphi) & + \sin(\varphi) \\ 0 & - \sin(\varphi) & + \cos(\varphi) \end{array} \right) \tag{22}\]
\[R_2(\varphi) = \left( \begin{array}{ccc} + \cos(\varphi) & 0 & - \sin(\varphi) \\ 0 & 1 & 0 \\ + \sin(\varphi) & 0 & + \cos(\varphi) \end{array} \right) \tag{23}\]
\[R_3(\varphi) = \left( \begin{array}{ccc} + \cos(\varphi) & + \sin(\varphi) & 0 \\ - \sin(\varphi) & + \cos(\varphi) & 0 \\ 0 & 0 & 1 \end{array} \right)\tag{24}\]
Determinante
Die Determinante ist der skalare Wert einer Matrix. Die Regel von Sarrus berechnet die Determinante (Abb. 3) wie folgt:
Die ersten beiden Spalten der Matrix werden rechts nochmals angeschrieben. Entlang der grünen und roten Pfeile werden die Werte multipliziert. Die drei grünen Produkte werden addiert und die drei roten Produkte anschließend subtrahiert.
\[\det(\mathbf{M}) = \left| \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right| = \begin{array}{c} \color{green}{+ a_{11} \cdot a_{22}\cdot a_{33} + a_{12}\cdot a_{23}\cdot a_{31} + a_{13}\cdot a_{21}\cdot a_{32}} \\ \color{red}{- a_{31}\cdot a_{22}\cdot a_{13} - a_{32}\cdot a_{23}\cdot a_{11} - a_{33}\cdot a_{21}\cdot a_{12}} \end{array}\tag{25}\]
Invertierte Matrix
Die Invertierung (Umkehrung) der Matrix M erfolgt mit Hilfe der Cramerschen Regel: Die Bildung einer Unterdeterminante N$_{ik}$ durch das Herausstreichen der i - ten Spalte und k - ten Zeile. \[\det(N_{ik}) = (-1)^{i+k} \mathbf{M} \quad und \quad b_{ik} = \frac{\det(N_{ik})}{\det(M)}\tag{26}\]
det($N_{ik}$) ist eine Streich- oder Unterdeterminante von M. Sie wird aus M gebildet, wenn die i - te Zeile und die k - te Spalte gestrichen wurde. Bei einer 3 $\times$ 3 Matrix sind es neun Unterdeterminanten $b_{ik}$. Die invertierte Matrix ist dann: \[M^{-1} = \frac{1}{\det(M)} \left(\begin{array}{ccc} b_{11} & b_{21} & b_{31} \\ b_{12} & b_{22} & b_{32} \\ b_{13} & b_{23} & b_{33} \end{array}\right)\tag{27}\]
Für die oben genannten Drehmatrizen gilt $R^{-1}(\varphi) = R(-\varphi)$.
Transponierte Matrix
Hat man eine Matrix M \[\mathbf{M} = \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right)\tag{28}\]
so ist die transponierte Matrix $M^t$: \[\mathbf{M}^t = \left( \begin{array}{ccc} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{array} \right)\tag{29}\]
Es vertauschen sich alle Elemente bis auf die Diagonalelemente gegenseitig. Überträgt man die transponierte Matrix $M^t$ auf die Drehmatrix $R(\varphi)$, so zeigt sich, daß $R^t(\varphi)$ = $R(-\varphi)$ gilt.
Interpolation
Taylorpolynom
Das Taylorpolynom (auch Taylorreihe/-entwicklung) ist die beliebteste Anwendung zur Näherung von Funktionen an der Stelle $r_0$ mit $|\vec{r} - \vec{r}_0| \ll 1$. \[f_{r_0}(\vec{r}) = f(\vec{r}_0) + f'(\vec{r}_0) \cdot (\vec{r} - \vec{r}_0) + \frac{1}{2} \cdot f''(\vec{r}_0) \cdot (\vec{r} - \vec{r}_0)^2 + \cdots = \sum_{k = 0}^{\infty} \frac{1}{k!} \cdot \frac{d^k}{d\vec{r}_0^k} f(\vec{r}_0) \cdot(\vec{r} - \vec{r}_0)^k\tag{30}\]
Ein Rechenbeispiel sind die trigonometrischen Funktionen und die e-Funktion: \[\begin{split} e^{\pm\varphi} &= 1 \pm \frac{\varphi}{1!} - \frac{\varphi^2}{2!} \mp \frac{\varphi^3}{3!} + \frac{\varphi^4}{4!} \pm \frac{\varphi^5}{5!} - ...= \sum_{n=0}^\infty \frac{\varphi^n}{n!} \\ \cos(\varphi) &= 1 - \frac{\varphi^2}{2!} + \frac{\varphi^4}{4!} - ... = \sum_{n=0}^\infty \frac{(-1)^n \varphi^{2n}}{(2n)!} \\ \sin(\varphi) &= \varphi - \frac{\varphi^3}{3!} + \frac{\varphi^5}{5!} - ... = \sum_{n=0}^\infty \frac{(-1)^n \varphi^{2n+1}}{(2n+1)!} \end{split}\tag{31}\]
Stirling-Interpolation
| $x_1 = x_0 - 2\cdot h$ | $y_1 = f(x_0 - 2\cdot h)$ | ||||
| $\nabla^{1} f\left(x_0 - \frac{3}{2}\cdot h\right)$ | |||||
| $x_2 = x_0 - h$ | $y_2 = f(x_0 - h)$ | $\nabla^{2} f(x_0 - h)$ | |||
| $x = x_0 - t\cdot h$ | $\nabla^{1} f\left(x_0 - \frac{1}{2}\cdot h\right)$ | $\nabla^{3} f\left(x_0 - \frac{1}{2}\cdot h\right)$ | |||
| $x_3 = x_0$ | $y_3 = f(x_0)$ | $\delta^{2} f(x_0)$ | $\delta^{4} f(x_0)$ | ||
| $x = x_0 + t\cdot h$ | $\Delta^{1} f\left(x_0 + \frac{1}{2}\cdot h\right)$ | $\Delta^{3} f\left(x_0 + \frac{1}{2}\cdot h\right)$ | |||
| $x_4 = x_0 + h$ | $y_4 = f(x_0 + h)$ | $\Delta^{2} f(x_0 + h)$ | |||
| $\Delta^{1} f\left(x_0 + \frac{3}{2}\cdot h\right)$ | |||||
| $x_5 = x_0 + 2\cdot h$ | $y_5 = f(x_0 + 2\cdot h)$ | ||||
$\Delta f(x_0) = f(x_0 + t \ h) - f(x_0)$ bilden die Vorwärtsdifferenzen und $\nabla f(x_0) = f(x_0) - f(x_0 - t \ h)$ sind die Rückwärtsdifferenzen. Die Hochzahlen bilden die Ordnungen; es sind keine Potenzen. Das gleiche gilt auch für die Zentraldifferenzen $\delta f(x_0) = f(x_0 + t \ h) - f(x_0 - t \ h)$.
Die entsprechende Interpolationsgleichung lautet $$f(x_0 \pm t h) = f(x_0) \pm t \cdot \delta^1 f(x_0) + \frac{t^2}{2} \cdot \delta^2 f(x_0) \pm \frac{(t + 1) t (t - 1)}{6} \cdot \delta^3 f(x_0) + \frac{(t + 1) t^2 (t - 1)}{24} \cdot \delta^4 f(x_0) \pm \cdots\tag{32}$$
mit \[\begin{align} \delta^1 f(x_0) &= \frac{1}{2} (\nabla^1 f(x_0 - \frac{1}{2} h) + \Delta^1 f(x_0 + \frac{1}{2} h)) \\ \delta^3 f(x_0) &= \frac{1}{2} (\nabla^3 f(x_0 - \frac{1}{2} h) + \Delta^3 f(x_0 + \frac{1}{2} h)) \end{align}\tag{33}\]
Eine Anwendungsmöglichkeit ist die Bestimmung der mittleren Bahnelemente aus den oskulierenden Bahnelementen. Diese sind jedoch nur innerhalb des Interpolationszeitraums gültig.
weitere Interpolationsverfahren
Die Interpolation hat aufgrund ihres Umfangs eine eigene Seite erhalten.
Komplexe Zahlen
Komplexe Zahlen entstehen, wenn Quadratwurzeln negative Argumente bei der Berechnung erhalten. Diese werden dann mit $i = \sqrt{-1}$ dargestellt. Eine komplexe Zahl $z$ setzt sich aus einem imaginären Anteil $b$ und einem realen Anteil $a$ zusammen: $$z = a + i\cdot b \qquad\text{mit}\qquad i = \sqrt{-1}\tag{34}$$
Für $i$ gilt:
- $i^{-1} = \frac{1}{i} = -i$,
- $i^2 = -1$,
- $i^3 = -i$,
- $i^4 = 1$,
- $i^5 = i$.
Tritt die Variante $$z^{*} = a - i\cdot b\tag{35}$$
auf, so bezeichnet man diese Zahl als konjungiert komplex zu $z$.
$$\text{real:} \qquad (a + b)(a - b) = a^2 + ab - ba - b^2 = a^2 - b^2\tag{36}$$ $$\text{komplex:} \qquad (a + ib)(a - ib) = a^2 + a ib - ib a - i^2b^2 = a^2 + b^2\tag{37}$$
Es gilt $z\cdot z^{*} = a^2 + b^2$, eine reelle Zahl.
 Abb. 4: Eine komplexe Zahl z und ihre konjugiert komplexe Zahl z*
Abb. 4: Eine komplexe Zahl z und ihre konjugiert komplexe Zahl z*
Eine anschauliche Darstellung der komplexen Zahlen im Koordinatenkreuz. $z$ kann als ein um den Ursprung kreisenden Radius vorgestellt werden. $a$, $b$ und $z$ bilden die Seiten eines rechtwinkeligen Dreiecks. Die konjugiert komplexe Form ist die Spiegelung an der reellen Achse.