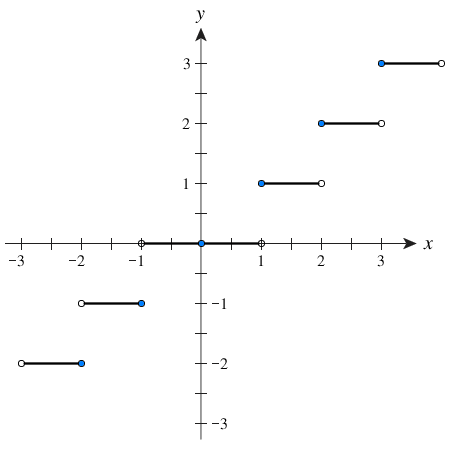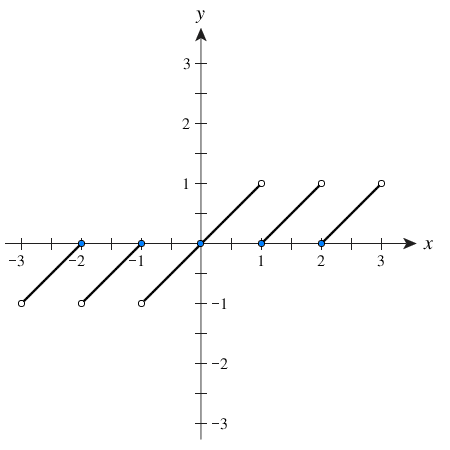−Inhaltsverzeichnis
Mathematische Grundlagen
In diesem Kapitel werden die wichtigsten Formeln - die hier im Wiki vorkommen - illustriert.
Grad- und Bogenmass
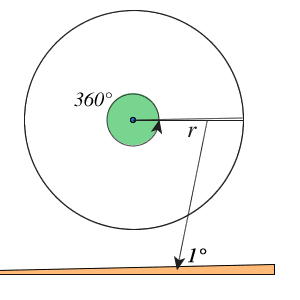
Gradmass
Ein voller Kreis wird in 360° geteilt. 1∘ ist dann logischerweise der 1360 Teil eines Vollkreises.
Mit Hilfe der Kreiszahl π=3.14159265… wird aus dem Bogenmass s das Gradmass α berechnet: α=180∘π⋅s
Diese Zahl ist dimensionslos, ihr Zeichen ist °.
Weitere Unterteilungen sind die Bogenminute ′ und die Bogensekunde ″:
- 1′ = 1 Bogenminute = 160 Teil eines Grades = 121600 Teil eines Vollkreises
- 1″ = 1 Bogensekunde = 160 Teil einer Bogenminute = 11296000 Teil eines Vollkreises
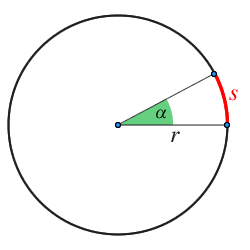
Bogenmass
Das Bogenmass eines Winkels α ist definiert als das Verhältnis der Länge des Kreisbogens s zum Radius r. Der Vollkreis, also der gesamte Bogen des Kreises (Umfang) lautet 2πr. Das Bogenmass für den Vollkreis lautet daher 2πrr=2π.
Die Umkehrung erfolgt mit der Gleichung: s=π180∘⋅α
Die Bezeichnung lautet Radian (englisch) bzw. Radiant und ihr Wert ist dimensionslos.
Tabelle Grad/Radiant
| Tabelle 1 | |
|---|---|
| Grad | Radiant |
| 0∘ | 0 |
| 30∘ | π6 |
| 45∘ | π4 |
| 60∘ | π3 |
| 90∘ | π2 |
| 180∘ | π |
| 270∘ | 3π2 |
| 360∘ | 2π |
Betrags- und Vorzeichenfunktion
Diese beiden Funktionen bestimmen das Vorzeichen einer Zahl.
Betragsfunktion
Der Absolutwert einer Variablen x wird durch die Betragsfunktion |x| bestimmt, die häufig auch als abs(x) bezeichnet wird. |x|={+x−xfallsx≥0x<0
Vorzeichenfunktion
Das Vorzeichen einer Variablen x wird durch die Signumsfunktion sgn(x) bestimmt. sgn(x)={+1−10fallsx>0x<0x=0
Floor und Ceiling Funktion
Floor Funktion
Volle Punkte gehören zur Funktion, leere Punkte hingegen nicht.
Die floor-Funktion bestimmt die nächstkleinere ganze Zahl (floor ⇒ englisch für „Boden“)
floor(x)=⌊x⌋
Beispiele:
floor(1.9)=1
floor(1.1)=1
floor(−1.1)=−2
floor(−1.9)=−2
Die Floor-Funktion hat noch etliche andere Bezeichnungen, z.B. Int-Funktion, Gauss- oder Entierklammer.
Ceiling Funktion
Die Ceilingfunktion bestimmt die nächstgrössere ganze Zahl (ceiling ⇒ englisch für „Decke“).
ceil(x)=⌈x⌉
Beispiele:
ceil(1.9)=2
ceil(1.1)=2
ceil(−1.1)=−1
ceil(−1.9)=−1
Die Ceiling-Funktion hat keine alternativen Bezeichnungen.
Trunc und Frac Funktion
Trunc Funktion
Die Trunc-Funktion gibt den ganzzahligen Wert einer Zahl wieder. Die Nachkommastellen werden abgeschnitten.
trunc(x)=fix(x)
Beispiele:
trunc(1.2345)=1
trunc(−1.2345)=−1
trunc(−0.6789)=0
Die trunc-Funktion wird gelegentlich auch als int-Funktion oder fix-Funktion bezeichnet.
Vorsicht geboten ist bei negativen Zahlen. Während für positive Zahlen die Funktionen floor(x) und trunc(x) dasselbe Ergebnis liefern, ist das bei negativen Zahlen nicht so:
Beispiel für JavaScript
console.log(Math.floor(298.99785)) // => 298 (nächstkleinere Ganzzahl) console.log(Math.trunc(298.99785)) // => 298 (Kommastellen abgeschnitten) console.log(Math.floor(-298.99785)) // => -299 (nächstkleinere Ganzzahl) console.log(Math.trunc(-298.99785)) // => -298 (Kommastellen abgeschnitten)
Frac Funktion
Die frac-Funktion gibt nur den Nachkommawert einer Zahl wieder. Die Vorkommastellen werden abgeschnitten.
frac(x)={x}=x−trunc(x)
Beispiele:
frac(1.2345)=0.2345
frac(−1.2345)=−0.2345
Reduktions- und Rundungsfunktion
Reduktionsfunktion
Mit Hilfe der Reduktionsfunktion kann ein Wert x auf ein Intervall zwischen 0 und y, −y und 0 oder auch auf ein Wert zwischen −y und +y reduziert werden. Das ist wichtig, wenn man mit Werten von >360∘, >24h oder <0∘, bzw. <0h zu tun hat. Es gilt:
red1=x−⌊xy⌋⋅y∀x≥0 red1=x−⌈xy⌉⋅y∀x≤0
Diese beiden Gleichungen reduzieren den Wert x auf ein Intervall [0,y] (oben) und [−y,0] (unten). Die nachfolgende Gleichung reduziert auf ein Intervall von [−y,y].
red2(x)=x−trunc(xy)⋅y
Beispielcode für JavaScript und Python
// JavaScript
function red(deg) {
return (deg % 360 + 360) % 360;
}
Die Funktion übernimmt eine dezimale Winkelgrösse deg und ermittelt mithilfe der Modulo-Funktion % das Intervall von [0°-360°]. Durch die 2-malige Verwendung der Modulo-Funktion ist der obige Ausdruck auch für negative Zahlen gültig.
# Python
def red(deg):
return (deg % 360 + 360) % 360
Rundungsfunktion
Die Rundungsfunktion spielt im Zusammenhang mit der Genauigkeit eine Rolle.
round(x,y)=⌊10yx+0.5⌋10−y∀x≥0 round(x,y)=⌈10yx+0.5⌉10−y∀x≤0
Diese Funktion rundet den Wert x auf y Stellen hinter dem Komma. Es handelt sich um die sogenannte kaufmännische Rundung.
Sexagesimalsystem
Das Sexagesimalsystem ist eine formatierte Ausgabe, basierend auf dem 160 Teil der Zahl W. Die Konvertierung vom Dezimalsystem zum Sexagesimalsystem ist folgender: Man startet mit W in Umdrehungen oder Tagen. Liegt W jedoch in Grad oder Stunden vor, so ist der Wert vorab entsprechend durch 360∘ bzw. 24h zu teilen. Ggf. überspringt man a und macht mit b weiter.
| Tabelle 2 | |
|---|---|
| W als Winkelwert | W als Zeitwert |
| a=trunc(|W|) | a=trunc(|W|) |
| b=trunc(360∘⋅frac(|W|)) | b=trunc(24h⋅frac(|W|)) |
| c=trunc(60′⋅frac(360∘⋅frac(|W|))) | c=trunc(60m⋅frac(24h⋅frac(|W|))) |
| d=60″⋅frac(60′⋅frac(360∘⋅frac(|W|))) | d=60s⋅frac(60m⋅frac(24h⋅frac(|W|))) |
Mit V=sgn(W) lautet die Ausgabe Varb∘c′d″ bzw. Vadbhcmds, wobei ar die Anzahl der Umdrehungen oder Umläufe ist. Dabei wird a eher selten praktisch verwendet.
Trigonometrische Funktionen
Diese Funktionen berechnen den Winkel innerhalb einer geometrischen Abbildung, z.B. einem rechtwinkeligen Dreieck.
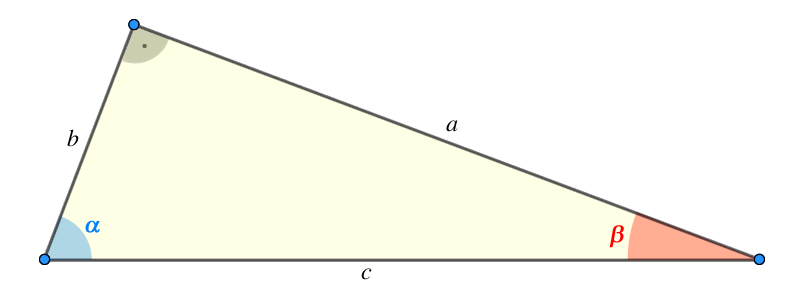 Abb. 7: Rechtwinkeliges Dreieck
Abb. 7: Rechtwinkeliges Dreieck
c= Hypotenuse (immer dem rechten Winkel gegenüber liegend)
a,b= Katheten
a= Gegenkathete von α= Ankathete von β
b= Gegenkathete von β= Ankathete von α
Sinus und Arcussinus
sin(α)=ac,sin(β)=bc
Umkehrfunktion:
arcsin(ac)=α,arcsin(bc)=β
arcsin(…) wird manchmal auch zu asn(…) abgekürzt.
Cosinus und Arcuscosinus
cos(α)=ac,cos(β)=bc
Umkehrfunktion:
arccos(ac)=α,arccos(bc)=β
arccos(…) wird manchmal auch zu acs(…) abgekürzt.
Tangens und Arcustangens
tan(α)=ab,tan(β)=ba
Umkehrfunktion:
arctan(ab)=α,arctan(ba)=β
arctan(…) wird manchmal auch zu atn(…) abgekürzt.
In den gängigen Programmiersprachen werden die Argumente von trigonometrischen Funktionen sin, cos, tan immer in Radiant (Bogenmass) verlangt. Viele Algorithmen auf diesen Seiten verwenden Winkelangaben in Grad. Man sollte daher nicht vergessen, diese Gradwerte mittels Multiplikation mit π180 in Radiant umzurechnen!
Wichtige Werte und Zusammenhänge
Es ist
tan(x)=sin(x)cos(x)
und der „trigonometrische Pythagoras“ lautet
sin2(x)+cos2(x)=1
 Abb. 8: Einheitskreis, Bezeichnungen, Quadranten
Abb. 8: Einheitskreis, Bezeichnungen, Quadranten
Folgende Werte für die Winkelfuntionen werden häufig benötigt:
| Tabelle 3 | |||
|---|---|---|---|
| Winkel | sin | cos | tan |
| 0∘ˆ=0rad | 0 | 1 | 0 |
| 30∘ˆ=π6 | 12 | √32 | 1√3 |
| 45∘ˆ=π4 | √22 | √22 | 1 |
| 60∘ˆ=π3 | √32 | 12 | √3 |
| 90∘ˆ=π2 | 1 | 0 | nicht def. |
Die wichtigsten Identitäten zwischen den trigonometrischen Funktionen sind folgende:
| Tabelle 4 | |||
|---|---|---|---|
| Funktion | ausgedrückt durch | ||
| sin | cos | tan | |
| sin(x) | sin(x) | ±√1−cos2(x) | ±tan(x)√1+tan2(x) |
| cos(x) | ±√1−sin2(x) | cos(x) | ±1√1+tan2(x) |
| tan(x) | ±sin(x)√1−sin2(x) | ±√1−cos2(x)cos(x) | tan(x) |
Umkehrfunktionen - Der richtige Quadrant
Dem Abschnitt über die quadrantentreue Darstellung hat eine eigene Seite bekommen, weil es es an dieser Stelle immer wieder zu Rechenfehlern kommt.
Sinus- und Cosinussatz im allgemeinen ebenen Dreieck
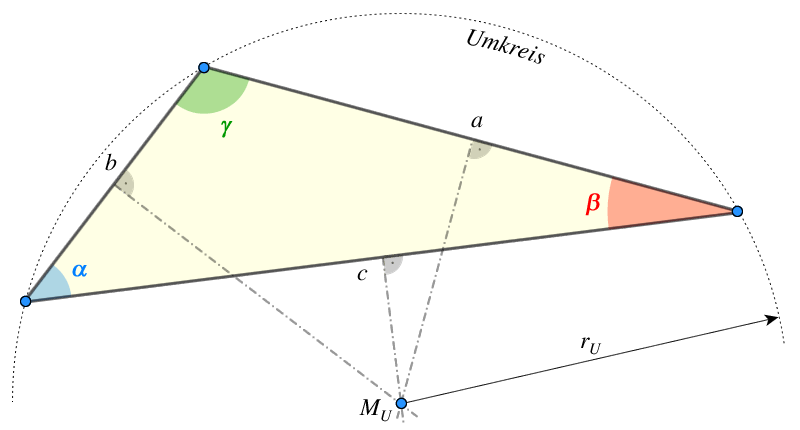
In Abb.9 sind a, b und c die Seiten eines ebenen Dreiecks, α, β und γ die jeweils gegenüberliegenden Winkel und rU der Radius des Umkreises.
Sinussatz
sin(α)a=sin(β)b=sin(γ)c=12⋅rU
Cosinussatz
a2=b2+c2−2⋅b⋅c⋅cos(α)b2=a2+c2−2⋅a⋅c⋅cos(β)c2=a2+b2−2⋅a⋅b⋅cos(γ)
Hyperpolische trigonometrische Funktionen
Zur Darstellung der hyperbolischen Bahnen werden Hyperbelfunktionen benötigt. Sie basieren wie die Sinus- und Cosinusfunktionen auf der Eulerzahl e aus der Exponentialfunktion. Auch deren Umkehrfunktionen Areasinus oder Areacosinus werden hier wiedergegeben.
 Abb. 10: Graphen des hyperbolischen Sinus, Cosinus und Tangens
Abb. 10: Graphen des hyperbolischen Sinus, Cosinus und Tangens
Definition
Wie bei den normalen trigonometrischen Funktionen können die Hyperbelfunktionen mit einer Taylorreihe approximiert werden:
e±x=N∑n=0(±x)kk!=x00!±x11!±x22!±x33!±x44!±…=1±x±x22±x36±x424±…
Hyperbelsinus
sinh(x)=ex−e−x2=x+x33!+x55!+x77!+…
Hyperbelcosinus
cosh(x)=ex+e−x2=1+x22+x44+x66!+…
Hyperbeltangens
tanh(x)=sinh(x)cosh(x)=ex−e−xex+e−x=x−x33+2x515−17x7315+…
Umkehrfunktionen
Die Umkehrfunktionen werden als Areasinus, Areacosinus und Areatangens bezeichnet. Sie sind mittles dem natürlichen Logarithmus wie folgt darstellbar:
arsinh(x)=ln(x+√x2+1)arcosh(x)=ln(x−√x2−1)x≥1artanh(x)=12⋅ln(1+x1−x)∀x≠1
Zusammenhänge zwischen den Hyperbelfunktionen
Aus den Reihenentwicklungen der Hyperbelfunktionen ergeben sich folgende Gleichungen. Die erste Gleichung wird auch als Eulersche Identität bezeichnet.
| cosh2(x)−sinh2(x)=1 | cosh(x)±sin(x)=e±x |
| cosh(arsinh(x))=√x2+1 | sinh(arcosh(x))=√x2−1 |
| cosh(i⋅x)=cos(x) | sinh(i⋅x)=sin(x) |
Exponentialfunktion
Die e-Funktion oder auch natürliche Exponentialfunktion beruht auf der eulerschen Zahl.
 Abb. 11: Die Exponentialfunktionen zur Basis e
Abb. 11: Die Exponentialfunktionen zur Basis e
exp(x)=∞∑n=0xnn!=1+x+x22!+x33!+x44!+…=1+x+x22+x36+x424+…
exp(−x)=∞∑n=0(−1)n⋅xnn!=1−x+x22!−x33!+x44!−…=1−x+x22−x36+x424−…
Logarithmus
Der natürliche Logarithmus ist die Umkehrfunktion zur oben genannten Exponetialfunktion.
 Abb. 12: Logarithmen zur Basis e und Basis 10
Abb. 12: Logarithmen zur Basis e und Basis 10
ln(x)=∞∑n=1(−1)n−1⋅(x−1)nn=(x−1)−(x−1)22+(x−1)33−(x−1)44+…∀x>0
log10(x)=1ln(10)⋅ln(x)=1ln(10)⋅∞∑n=1(−1)n−1⋅(x−1)nn∀x>0
Logarithmus Rechenregeln
Es gilt für jeden Logarithmus zu einer beliebigen Basis b:
logb(x⋅y)=logb(x)+logb(y)
logb(xy)=logb(x)−logb(y)
logb(xy)=y⋅logb(x)
Basisumrechnung
Die Basis des Logarithmus kann gewechselt werden, indem man durch den Logarithmus der alten Basis teilt:
logb(x)=loga(x)loga(b)
Insbesondere gilt für den Wechsel zum natürlichen Logarithmus:
ln(x)=loga(x)loga(e)
Sphärische Trigonometrie
Die sphärische Trigonometrie wird unter anderem in der Transformation der Koordinaten gebraucht. Die geometrische Definition der Grosskreise ist die Schnittlinie zwischen einer Kugel und einer Ebene, die durch den Mittelpunkt M der Kugel verläuft.
 Abb. 13: Das sphärische Dreieck
Abb. 13: Das sphärische Dreieck
Verbindet man drei Punkte auf einer Kugeloberfläche durch Grosskreisestücke, so erhält man ein sphärisches Dreieck wie in Abb.13 dargestellt. Es wird beschrieben durch die Winkel a, b und c, unter denen die Eckpunkte vom Kugelmittelpunkt M aus erscheinen (kurz Seiten genannt) und die Winkel α, β und γ, unter denen sich diese Grosskreisestücke in den Eckpunkten schneiden.
Der Cosinussatz im sphärischen Dreieck
Der Seiten-Cosinussatz lautet:
cos(a)=cos(b)⋅cos(c)+sin(b)⋅sin(c)⋅cos(α)cos(b)=cos(c)⋅cos(a)+sin(c)⋅sin(a)⋅cos(β)cos(c)=cos(a)⋅cos(b)+sin(a)⋅sin(b)⋅cos(γ)
Der Winkel-Cosinussatz lautet:
cos(α)=sin(β)⋅sin(γ)⋅cos(a)−cos(β)⋅cos(γ)cos(β)=sin(γ)⋅sin(α)⋅cos(b)−cos(γ)⋅cos(α)cos(γ)=sin(α)⋅sin(β)⋅cos(c)−cos(α)⋅cos(β)
Der Sinussatz im sphärischen Dreieck
Der Sinussatz lautet:
sin(a)sin(α)=sin(b)sin(β)=sin(c)sin(γ)
Der Sinus-Cosinus Satz im sphärischen Dreieck
Die Seiten-Winkel Gleichungen: sin(a)⋅cos(β)=cos(b)⋅sin(c)−sin(b)⋅cos(c)⋅cos(α)sin(b)⋅cos(γ)=cos(c)⋅sin(a)−sin(c)⋅cos(a)⋅cos(β)sin(c)⋅cos(α)=cos(a)⋅sin(b)−sin(a)⋅cos(b)⋅cos(γ)
Winkel-Seiten Gleichungen: sin(α)⋅cos(b)=cos(β)⋅sin(γ)+sin(β)⋅cos(γ)⋅cos(a)sin(β)⋅cos(c)=cos(γ)⋅sin(α)+sin(γ)⋅cos(α)⋅cos(b)sin(γ)⋅cos(a)=cos(α)⋅sin(β)+sin(α)⋅cos(β)⋅cos(c)
karthesisch ↔ sphärisch
Die Umrechnung zwischen karthesisch und sphärisch ist wichtig bei den Koordinatentransformationen.
sphärisch → karthesisch
Die Umwandlung in die karthesischen Koordinaten ist einfach. Sei α die Länge in der x,y-Ebene und β die Breite über- oder unterhalb dieser Ebene. r ist der Abstand des Objekts vom Ursprung.
x=r⋅cos(β)⋅cos(α)y=r⋅cos(β)⋅sin(α)z=r⋅sin(β)
karthesisch → sphärisch
Die Umrechnung von karthesisch zu sphärisch ist komplexer, weil die quadrantenrichtige Darstellung berücksichtigt werden muss. Zunächst wird die Breite β bestimmt mit
β=arcsin(zr)mitr=√x2+y2+z2
dann erfolgt die Berechnung der Länge α mit Hilfe von φ. Es seien C bzw. S
C=xr⋅cos(β) S=yr⋅cos(β)
φ=arcsin(S)falls|S|<1 φ=arccos(C)falls|S|>1
Jetzt erfolgt die quadrantenrichtige Korrektur:
α={360∘−φ180∘−φfallsC>0undS<0C<0
Sonst gilt:
α=φ
Additionstheoreme
Um zwei Winkel α und β zu addieren oder zu subtrahieren werden die Additionstheoreme der trigonometrischen Funktionen benötigt. sin(α±β)=sin(α)⋅cos(β)±cos(α)⋅sin(β) cos(α±β)=cos(α)⋅cos(β)∓sin(α)⋅sin(β) tan(α±β)=tan(α)±tan(β)1∓tan(α)⋅tan(β)
Gilt α = β = φ, so wird zum nachfolgenden Ausdruck abgekürzt: sin(2⋅φ)=2⋅sin(φ)⋅cos(φ) cos(2⋅φ)=cos2(φ)−sin2(φ) tan(2⋅φ)=2⋅tanφ1−tan2(φ)
Mathematische Anwendungen
Weitere mathematische Anwendungen werden auf einer eigenen Seite behandelt.
Interpolation
Die Interpolation hat aufgrund ihres Umfangs eine eigene Seite erhalten.
Iteration
Auch die Iteration (also das Prinzip des rekursiven Einsetzens unter Einhaltung der Konvergenz) wird in einer eigenen Seite dokumentiert.