Die Mondlibration

Es ist eine bekannte Tatsache, dass der Mond immer die gleiche Seite zur Erde zeigt, sodass nie eine Hälfte der Mondoberfläche zu sehen ist. Tatsächlich ist dies nicht ganz genau: Die Mondkugel weist eine periodische Schwingung auf, die als Libration (lateinisch: librare = schwingen) bezeichnet wird. Demnach können von der Erde aus insgesamt etwa 59% der Mondoberfläche beobachtet werden. Beginnen wir mit der Darlegung der drei empirischen Gesetze, die die Rotation des Mondes beschreiben; Sie wurden 1693 von Giovanni Domenico Cassini (italienischer Astronom, 1625-1712) formuliert.

• 1. Gesetz: Der Mond dreht sich im direkten Sinne (d. h. im gleichen Sinne wie die Erde), mit einer konstanten Winkelgeschwindigkeit (in Bezug auf die Sterne), und die siderische Rotationsperiode ist gleich der mittleren siderischen Rotationsperiode Umlauf des Mondes um die Erde, der $27\overset{d}{.}32166$ Tage beträgt (23^d7^h43^m11.4^s).

• 2. Gesetz: Die Neigung $i$ der mittleren Ebene des Mondäquators zur Ebene der Ekliptik ist konstant. Laut F. Hayn (1907) beträgt diese Neigung $1^\circ 32' 06''$. Später leitete Hayn den verbesserten Wert $i = 1^\circ 32' 20''$ ab. C.B. Watts (1955) fand $1^\circ 33' 50''$, aber der derzeit von der Internationalen Astronomischen Union (IAU) angenommene Wert ist $i = 1^\circ 32'32\overset{''}{.}7$.

• 3. Gesetz: Die Rotationsachse des Mondes, die Achse der Ekliptik (also die Senkrechte zu dieser Ebene) und die Achse der Mondbahn (die Senkrechte zu seiner Ebene) liegen immer in derselben Ebene, und zwar in dieser Reihenfolge. Mit anderen Worten: Der Schnittpunkt der Äquatorialebene der Mondkugel mit der Ekliptik verläuft parallel zur Knotenlinie der Mondbahn; Der absteigende Knoten des Mondäquators fällt mit dem aufsteigenden Knoten der Umlaufbahn zusammen.

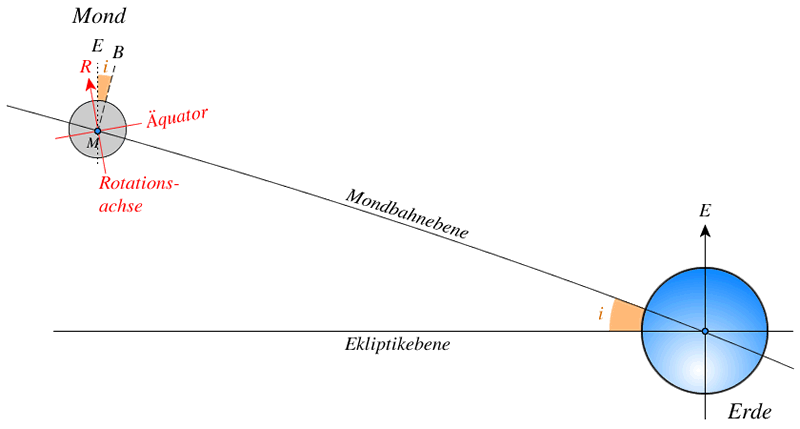
Wenn man das als zu kompliziert empfindet, kann man sich Abb.1 ansehen.

Abb. 1

In dieser Zeichnung sind die Durchmesser von Erde und Mond und ihr relativer Abstand nicht maßstabsgetreu! Die Ebene der Figur steht senkrecht zur Ebene der Erdumlaufbahn (Ekliptik) und auch zur Ebene der Mondbahn. $MR$ ist die Rotationsachse des Mondes, $ME$ steht senkrecht zur Ebene der Ekliptik und $MB$ steht senkrecht zur Ebene der Mondbahn. Das zweite Gesetz von Cassini besagt, dass der Winkel $\measuredangle RME$ konstant ist mit $1^\circ 32' 33''$. Das dritte Gesetz besagt, dass $MR$, $ME$ und $MB$ in derselben Ebene liegen, und zwar so, dass $MR$ und $MB$ gegenüberliegend in Bezug auf $ME$ sind. Der Winkel $\measuredangle EMB$ ist gleich der Neigung der Ebene der Mondbahn zur Ekliptik (Winkel $i$ in Abb.1), und der Mittelwert dieses Winkels beträgt $i = 5^\circ 09'$. Folglich ist die (mittlere) Neigung der Rotationsachse der Mondkugel zur Bahnebene des Mondes gleich

\[ \begin{align}\measuredangle RMB &= \measuredangle RME + \measuredangle EMB \\ &= 1^\circ 32' + 5^\circ 09' = 6^\circ 41' \end{align}\]

Im Weiteren unterscheidet man nun die Libration in Länge und die Libration in Breite.

Da der Mondäquator einen Winkel (Mittelwert $6^\circ 41'$) mit der Ebene der Mondumlaufbahn bildet, werden der Nord- und Südpol des Mondes während einer Mondumdrehung (ca. 27 Tage) abwechselnd zur Erde geneigt sein.

Im Fall von Abb.1 befindet sich der Mond nördlich der Ekliptik, etwa in der Mitte zwischen dem aufsteigenden und dem absteigenden Knoten seiner Umlaufbahn, sodass der Mond-Südpol der Erde zugewandt ist. Der Mondäquator (in der Zeichnung rot dargestellt) steht senkrecht zur Rotationsachse $MR$.

Zur mathematischen Beschreibung benötigt man als erstes die Neigung der Mondbahn gegen die Ekliptik mit $i = 5\overset{\circ}{.}15668983$ und die Neigung des Mondäquators gegen die Mondbahn mit $i_0 = 1\overset{\circ}{.}542416667^{\circ}$. Mit den geozentrisch ekliptikalen Koordianten $\lambda$ und $\beta$ kann man dann als nächstes die Libration der Breite mit $l'$ und $b'$ berechnen.

\[\begin{align} \cos(b') \cdot \cos(l' + F) &= x = \cos(\lambda - \Omega) \cdot \cos(\beta) \\ \cos(b') \cdot \sin(l' + F) &= y = \sin(\lambda - \Omega) \cdot \cos(\beta) \cdot \cos(i_0) - \sin(\beta) \cdot \sin(i_0) \\ \sin(b') &= z = \sin(\lambda - \Omega) \cdot \cos(\beta) \cdot \sin(i_0) + \sin(\beta) \cdot \cos(i_0) \end{align}\tag{1}\]

mit $F = l - \Omega$ als Argument der Breite.

Die Libration in Länge ergibt sich aus der Tatsache, dass sich die Mondkugel gleichmäßig dreht (konstante Winkelgeschwindigkeit), während die Geschwindigkeit des Mondes auf seiner Umlaufbahn um die Erde variabel ist. In der Nähe des Perigäums, wo der Abstand zur Erde am geringsten ist, ist die Umlaufgeschwindigkeit größer als in der Nähe des Apogäums, wo der Abstand zur Erde maximal ist.

Abb. 2

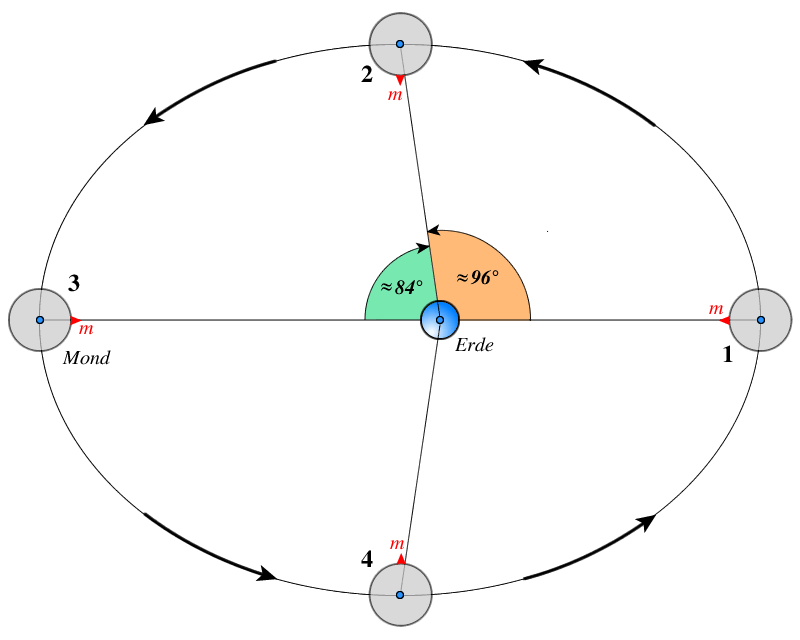
Abb.2 zeigt die Bewegung des Mondes um die Erde. Auch in dieser Abbildung sind die Durchmesser von Erde und Mond sowie die Abstände nicht maßstabsgetreu. In Position $1$ befindet sich der Mond im Perigäum. Sei $m$ zu diesem Zeitpunkt der Mittelpunkt der Mondscheibe (von der Erde aus gesehen). Man kann sich vorstellen, dass sich am Punkt $m$ ein großer Mondberg befindet, der zur Erde hin ausgerichtet ist.

Nach einer Vierteldrehung (das sind $\tfrac{27.32}{4} = 6.83$ Tage) hat sich die Mondkugel um genau $90^\circ$ gedreht. Der Mond hat dann Position $2$ erreicht. Diese Position ist nicht $90^\circ$, sondern etwa $96^\circ$ weiter in der Umlaufbahn als Position $1$, und Punkt $m$ scheint nun nach Osten (nach „links“) verschoben zu sein. Am westlichen Mondrand sehen wir etwas über den Rand der „mittleren“ sichtbaren Mondhälfte hinaus. Eine halbe Umdrehung nach dem Perigäum erreicht der Mond sein Apogäum und hat von der Erde aus gesehen über $180^\circ$ zurückgelegt – Position $3$ in Abb.2. Auch die Mondkugel hat sich nun um genau $180^\circ$ gedreht und der Punkt $m$ liegt somit von der Erde aus gesehen wieder genau im Zentrum der Mondscheibe.

Eine Vierteldrehung nach dem Apogäum hat sich Punkt $m$ um weitere $90^\circ$ in Bezug auf die Achse der Mondkugel gedreht. Aber der Mond hat sich nur über $84^\circ$ in Bezug auf die Erde bewegt, weil die Geschwindigkeit in diesem Teil seiner Umlaufbahn geringer ist als sein Mittelwert. Der Mond befindet sich jetzt in Position $4$ und wir sehen etwas über den mittleren östlichen Rand seiner Scheibe hinaus; Punkt $m$ ist nun etwas westlich („rechts“) der Scheibenmitte zu sehen. Nach einer weiteren Vierteldrehung ist der Mond mit erhöhter Geschwindigkeit ins Perigäum zurückgekehrt, und der Mondberg $m$ befindet sich, vom Erdmittelpunkt aus gesehen, wieder genau im Zentrum der sichtbaren Hälfte der Mondkugel.

Zur mathematischen Beschreibung braucht man die beiden Hilfswerte $K_1$ und $K_2$: $$K_1 = 119\overset{\circ}{.}75 + 131\overset{\circ}{.}849 \ T \\ K_2 = 72\overset{\circ}{.}56 + 20\overset{\circ}{.}186 \ T\tag{2}$$

Die Gleichungen zur Berechnung der Libration in Länge sind dann: \[\begin{array}{llll} \varrho = & - 0\overset{\circ}{.}02752 \ \cos(m) & - 0\overset{\circ}{.}02245 \ \sin(F) & + 0\overset{\circ}{.}00684 \ \cos(m - 2 \ F) \\ & - 0\overset{\circ}{.}00293 \ \cos(2 \ F) & - 0\overset{\circ}{.}00085 \ \cos(2 \ F - 2 \ D) & - 0\overset{\circ}{.}00054 \ \cos(m - 2 \ D) \\ & - 0\overset{\circ}{.}00020 \ \sin(m + F) & - 0\overset{\circ}{.}00020 \ \cos(m + 2 \ F) & - 0\overset{\circ}{.}00020 \ \cos(m - F) \\ & + 0\overset{\circ}{.}00014 \ \cos(m + 2 \ F - 2 \ D) & & \\ \sigma = & - 0\overset{\circ}{.}02816 \ \sin(m) & + 0\overset{\circ}{.}02244 \ \cos(F) & - 0\overset{\circ}{.}00682 \ \sin(m - 2 \ F) \\ & - 0\overset{\circ}{.}00279 \ \sin(2 \ F) & - 0\overset{\circ}{.}00083 \ \sin(2 \ F - 2 \ D) & - 0\overset{\circ}{.}00069 \ \sin(m - 2 \ D) \\ & + 0\overset{\circ}{.}00040 \ \cos(m + F) & - 0\overset{\circ}{.}00025 \ \sin(2 \ m) & - 0\overset{\circ}{.}00023 \ \sin(m + 2 \ F) \\ & + 0\overset{\circ}{.}00020 \ \cos(m - F) & + 0\overset{\circ}{.}00019 \ \sin(m - F) & - 0\overset{\circ}{.}00010 \ \cos(m - 3 \ F) \\ & + 0\overset{\circ}{.}00013 \ \sin(m + 2 \ F - 2 \ D) \\ \tau = & + 0\overset{\circ}{.}02520 \ E \ \sin(M) & + 0\overset{\circ}{.}00473 \ \sin(2 \ m - 2 \ F) & - 0\overset{\circ}{.}00467 \ \sin(m) \\ & + 0\overset{\circ}{.}00396 \ \sin(K_1) & + 0\overset{\circ}{.}00276 \ \sin(2 \ m - 2 \ D) & + 0\overset{\circ}{.}00196 \ \sin(\Omega) \\ & - 0\overset{\circ}{.}00183 \ \cos(m - F) & + 0\overset{\circ}{.}00115 \ \sin(m - 2 \ D) & - 0\overset{\circ}{.}00096 \ \sin(m - D) \\ & + 0\overset{\circ}{.}00046 \ \sin(2 \ F - 2 \ D) & - 0\overset{\circ}{.}00039 \ \sin(m - F) & + 0\overset{\circ}{.}00023 \ \sin(K_2) \\ & - 0\overset{\circ}{.}00012 \ \sin(m - 2 \ F) & + 0\overset{\circ}{.}00014 \ \cos(2 \ m - 2 \ F) & - 0\overset{\circ}{.}00014 \ \sin(2 \ D) \\ & + 0\overset{\circ}{.}00027 \ E \ \sin(2 \ m - M - 2 \ D) & + 0\overset{\circ}{.}00011 \ E^2 \ \sin(2 \ m - 2 \ M - 2 \ D) & - 0\overset{\circ}{.}00012 \ \sin(2 \ m) \\ & - 0\overset{\circ}{.}00032 \ E \ \sin(m - M - D) & & \end{array}\tag{3}\]

Die Libration in Länge $l''$ und $b''$ erhält man letztendlich mit: \[\begin{align} l'' &= - \tau + (\varrho \cos(l' + F) + \sigma\cdot\sin(l' + F))\cdot\tan(b')\\ b'' &= \varrho\cdot\cos(l' + F) - \sigma\cdot\sin(l' + F) \end{align}\tag{4}\]

Im Vorhergehenden wurde angenommen, dass sich der Beobachter im Mittelpunkt der Erde befindet. Ein tatsächlicher Beobachter $B$ befindet sich jedoch an der Erdoberfläche. Daher bildet die Richtung, aus der er auf den Mond schaut, einen Winkel mit der Linie, die die Mittelpunkte von Erde und Mond verbindet (Abb.3). Für diesen Beobachter ist der Mittelpunkt $O$ der Mondscheibe nicht derselbe Punkt des Mondglobus wie der Mittelpunkt $m$ für einen geozentrischen Beobachter. Dieser topozentrische Effekt, der ca. $1^\circ 02'$ erreichen kann, variiert im Tagesverlauf, da sich der Beobachter mit der Erdoberfläche mitdreht (Erdrotation). Aus diesem Grund wird der Effekt als Tages-Libration bezeichnet.

Abb. 3

Die oben beschriebenen Längen- und Breiten-Librationen sind zusammen mit der Tages-Libration keine wirklichen Schwingungen der Mondkugel: Sie sind lediglich scheinbare Librationen für einen Beobachter auf der Erde. Aus diesem Grund werden sie optische Librationen genannt. Es gibt jedoch eine echte Schwingung der Mondkugel. Diese physikalische Libration ist eine Unregelmäßigkeit der Rotation des Mondes in Bezug auf seine mittlere Rotationsgeschwindigkeit. Dies ergibt sich aus der Tatsache, dass der Durchmesser der der Erde zugewandten Mondkugel etwas größer ist als der mittlere Durchmesser des Mondes. Dieser sehr kleine „Vorsprung“ wird von der Erde angezogen und verursacht eine Schwingung der Mondkugel. Diese physikalische Libration ist viel kleiner als die optische Libration und überschreitet niemals $2'$ in der Länge und $3'$ in der Breite.

Die topozentrische Libration $\Delta l$ und $\Delta b$ wird durch die topozentrischen Koordinaten des Mondes $\alpha'$ und $\delta'$ bestimmt.

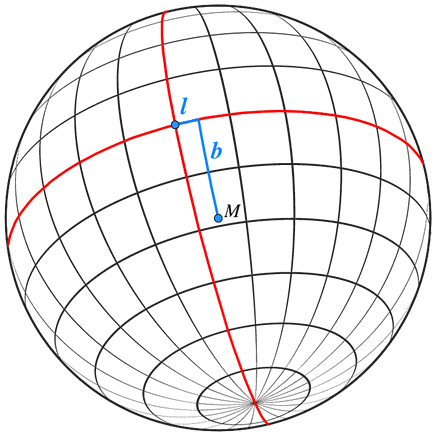Abb. 4 Der mittlere Punkt $M$ stellt den Mittelpunkt der Mondscheibe dar, wie sie rein optisch am Himmel zu sehen ist. Die roten Linien sind Äquator bzw. Meridian. Die Libration in Länge ist dann das Maß $l$ und die Libration in Breite ist $b$. J. Meeus unterscheidet die optische Libration mit $l',\;b'$ und die physische Libration mit $l'',\;b''$.

Die gesamte Libration berechnet sich dann mit

\[\begin{align} l &= l' + l'' + \Delta l\\ b &= b' + b'' + \Delta b \end{align}\tag{5}\]

$+b$ bedeutet der Nordpol ist dem Beobachter zugewandt und $+l$ bedeutet man sieht mehr von der Westseite (Mond libriert nach Ost). Die Abb.4 hat damit $+l,\;-b$. Die vier Kombinationen von $l$ und $b$ sind hier nochmals gegenübergestellt:

Libration nach Nord und nach Ost	Libration nach Nord und nach West
$+l,\;-b$	$-l,\;-b$
Libration nach Süd und nach Ost	Libration nach Süd und nach West
$+l,\;+b$	$-l,\;+b$