Inhaltsverzeichnis
Interpolation
Astronomische Jahrbücher oder andere Publikationen enthalten meist numerische Tabellen, in denen bestimmte Größen $y$ für äquidistante Werte eines Argumentes $x$ gegeben sind. Zum Beispiel kann $y$ die Rektaszension $\alpha_{\odot}$ der Sonne und $x$ der Tag des Jahres um $\textrm{00:00}\;TD$ sein.
Interpolation (Latein: inter = dazwischen und polire = glätten, schleifen) bedeutet das Finden der Werte von Größen – zum Beispiel von Zeitpunkten – die zwischen den in der Tabelle gegebenen Werten liegen.
Natürlich muss die Tabelle nicht aus einem Buch stammen, die Werte können auch aus einem computergenerierten Algorithmus kommen. Angenommen, man benötigt die Position der Sonne für viele Zeitpunkte eines Tages. Dann könnte man die Sonnenposition für $0^h$, $12^h$ und $24^h$ dieses Tages berechnen und diese Werte dann benutzen, um für jeden anderen gegebenen Zeitpunkt zu interpolieren. Das wird weniger Rechenzeit beanspruchen, als die Position der Sonne direkt für jeden Zeitpunkt einzeln zu berechnen.
Nachstehend werden zwei Fälle betrachtet: Die Interpolation mit drei oder mit fünf Tabellenwerten. In beiden Fällen wird auch gezeigt, wie ein Extremum oder eine Nullstelle der Funktion gefunden werden kann.
Der Fall für zwei Tabellenwerte wird hier nicht behandelt, weil in diesem Fall die Interpolation nichts anderes als linear sein kann, was keinerlei Schwierigkeiten bringen dürfte.
Interpolation mit drei Tabellenwerten
Drei Tabellenwerte $y_1$, $y_2$ und $y_3$ der Funktion $y = f(x)$ sind gegeben, die zu den Werten $x_1$, $x_2$ und $x_3$ des Arguments $x$ gehören.
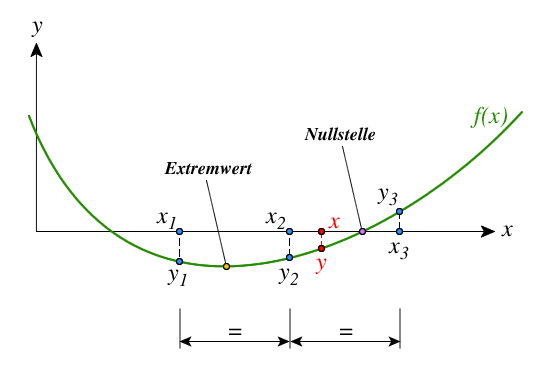Abb. 1: Interpolation mit 3 Tabellenwerten
Die Tabelle der Differenzen sei dann
| Tabelle 1 | |||
|---|---|---|---|
| Argument | Funktionswert | Differenz 1. Ordnung | Differenz 2. Ordnung |
| $x_1$ | $y_1$ | ||
| $a = y_2 - y_1$ | |||
| $x_2$ | $y_2$ | $c = y_1 + y_3 - 2\cdot y_2$ | |
| $b = y_3 - y_2$ | |||
| $x_3$ | $y_3$ | ||
Für gewöhnlich werden die Differenzen aufeinander folgender Ordnungen allmählicher kleiner. Die Interpolation aus drei Werten ist erlaubt, wenn die Differenzen 1. Ordnung fast konstant, und daher die Differenzen 2. Ordnung fast Null sind.
Es gilt nun für den gesuchten Wert:
$$y = y_2 + \frac{n}{2}\cdot (a + b + n\cdot c)$$
wobei $n$ der Interpolationsfaktor ist (siehe Beispiel).
Hier ist etwas Fingerspitzengefühl erforderlich. Die Mondposition kann z.B. aus drei Positionen in stündlichen Intervallen sehr gut interpoliert werden, nicht jedoch, wenn das Intervall ein ganzer Tag ist!
Sucht man einen Extremwert, also ein Minimum oder Maximum, kann dies über folgende Beziehungen ermittelt werden:
Der Minimal- bzw. Maximalwert ist
$$y_{\textrm{m}} = y_2 - \frac{(a + b)^2}{8\cdot c}$$
und der dazu gehörende Wert des Arguments $x$ ist zu ermitteln über
$$n_{\textrm{m}} = - \frac{(a + b)}{2\cdot c} $$
in Einheiten des Tabellenintervalls, gemessen vom zentralen Wert $x_2$.
Der Wert des Argumentes $x$, für den die Funktion $y = 0$ wird, kann wieder durch die Bildung der Differenzentabelle für den entsprechenden Teil der Tabelle gefunden werden. Der Interpolationsfaktor $n_0$, der der Nullstelle der Funktion entspricht, ist gegeben durch die Formel
$$n_0 = \frac{-2\cdot y_2}{a + b + c\cdot n_0}$$
Diese Gleichung kann gelöst werden, indem man auf der rechten Seite zuerst $n_0 = 0$ setzt. Die Formel gibt dann einen genäherten Wert für $n_0$. Dieser Wert wird dann benutzt, um die rechte Seite erneut zu berechnen, wodurch sich ein noch besserer Wert für $n_0$ ergibt. Dieser Iterationsprozess wird solange wiederholt, bis sich der für $n_0$ gefundene Wert im Rahmen der gewünschten Genauigkeit nicht mehr ändert.
Die obige Berechnung des Interpolationsfaktors $n_0$, für den die Funktion Null ist, ist sehr gut geeignet, wenn die Funktion im entsprechenden Intervall annähernd linear verläuft. Bei starker Krümmung jedoch kann die Anwendung der Formel eine große Zahl von Iterationen erfordern oder sogar zu einer Divergenz führen, selbst wenn man mit einem fast korrekten Wert $n_0$ beginnt. In diesem Fall ist die folgende Methode zur Berechnung von $n_0$ besser:
Die Korrektur zum davor angenommenen Wert für $n_0$ ist
$$\Delta n_0 = -\frac{2\cdot y_2 + n_0\cdot (a + b + c\cdot n_0)}{a + b + 2\cdot c\cdot n_0}$$
Auch hier muss mit dem neuen Wert von $n_0$ die Rechnung so oft wiederholt werden, bis sich $n_0$ nicht mehr ändert.
Beispiel 1
Aus einem Jahrbuch kennt man die geozentrischen Abstände von Mars zur Erde für jeweils 00:00 $TD$ des Tages (siehe Tabelle). Man interpoliere die Entfernung des Mars am 23. Mai 2023 um 22:30 $TD$.
Tabelle für Mars, vom 21.-25. Mai 2023, 00:00 $TD$.
Die Werte sind in Astronomischen Einheiten $AU$ gegeben, die Differenzen in Einheiten von $10^{-6}\;AU$:
| Tag | Entfernung [AU] | Diff. 1. Ordnung | Diff. 2. Ordnung | Diff. 3. Ordnung |
|---|---|---|---|---|
| $21$ | $1.911859$ | |||
| $8238$ | ||||
| $22$ | $1.920097$ | $-46$ | ||
| $8192$ | $+2$ | |||
| $23$ | $1.928289$ | $-44$ | ||
| $8148$ | $-3$ | |||
| $24$ | $1.936437$ | $-47$ | ||
| $8101$ | ||||
| $25$ | $1.944538$ |
Man erkennt: Da die Differenzen 3. Ordnung fast Null sind, kann aus nur drei Tabellenwerten interpoliert werden.
Der zentrale Wert $x_2$ muss so gewählt werden, dass er dem gesuchten $x$-Wert am nächsten liegt. Hier wird der Abstand von Mars für den 23. Mai um $22^h 30^m\;TD$ benötigt, also dezimal gerechnet für den Wert
$23^d + \frac{\left(22^h + \tfrac{30^m}{60\tfrac{m}{h}}\right)}{24\tfrac{h}{d}} = 23\overset{d}{.}9375$
dann ist der zentrale Wert $x_2$ der Wert für den 24. Mai (liegt dem gesuchten Wert am nächsten) und $y_2 = 1.936437$. In diesem Fall muss man die gegebenen Tabellenwerte für den 23., 24. und 25. Mai nehmen, nämlich
$x_1 = 23$, $y_1 = 1.928289$
$x_2 = 24$, $y_2 = 1.936437$
$x_3 = 25$, $y_3 = 1.944538$
Die Differenzen in 1. und 2. Ordnung sind dann
$a = y_2 - y_1 = 0.008148$
$b = y_3 - y_2 = 0.008101$
$c = y_1 + y_3 - 2\cdot y_2 = -4.7\cdot 10^{-5}$
Es sei nun $n$ der Interpolationsfaktor, das heißt, man hat $n = x - x_2$ in Einheiten des Tabellenintervalls (hier 1 Tag = $24^h$), wenn $y$ der gesuchte Wert der Funktion für den Wert $x = 23\overset{d}{.}9375$ ist.
- Liegt der gesuchte $x$-Wert vor $x_2$, also $x \lt x_2$, ist $n$ negativ.
- Liegt der gesuchte $x$-Wert nach $x_2$, also $x \gt x_2$, ist $n$ positiv.
Wurde $y_2$ richtig gewählt, wird $n$ zwischen $-0.5$ und $+0.5$ liegen, obwohl die Interpolationsformel auch für alle Werte von $n$ zwischen $-1$ und $+1$ korrekte Resultate liefern würde. Im vorliegenden Fall ist
$n = x - x_2 = 23.9375 - 24 = -0.0625$
in Einheiten des Tabellenintervalls. Die Interpolationsformel lautet
$y = y_2 + \frac{n}{2}\cdot (a + b + n\cdot c)$
daher folgt
| \(\begin{align} y &= 1.936437 + \frac{-0.0625}{2}\cdot \bigg(0.008148 + 0.008101 + (-0.0625\cdot -4.7\cdot 10^{-5})\bigg)\\ &= 1.935929 \end{align}\) |
Der Abstand von Mars zur Erde am 23. Mai 2023 um 22:30 $TD$ ist $\Delta = 1.935929\;AU$.
Das JPL HORIZONS gibt für den gesuchten Zeitpunkt den Wert $\Delta = 1.93592868581821\;AU$ aus.
Beispiel 2
Man berechne die Zeit des Periheldurchgangs von Mars im Mai 1992 sowie seinen Radiusvektor $\Delta$ zu diesem Zeitpunkt.
Die folgenden Werte der Entfernung Sonne-Mars wurden in Intervallen von vier Tagen berechnet:
| Zeitpunkt | Entfernung in $AU$ |
|---|---|
| 12. Mai 1992, 00:00 $TD$ | $1.381430$ |
| 16. Mai 1992, 00:00 $TD$ | $1.381222$ |
| 20. Mai 1992, 00:00 $TD$ | $1.381245$ |
Der zentrale Wert $x_2$ ist hier der 16. Mai 1992 um 00:00 $TD$, mit dem dazu gehörenden $y_2 = 1.381222$.
Die Differenen 1. und 2. Ordnung sind
$a = y_2 - y_1 = -2.08\cdot 10^{-4}$
$b = y_3 - y_2 = +2.3\cdot 10^{-5}$
$c = y_1 + y_3 - 2\cdot y_2 = +2.31\cdot 10^{-4}$
Daraus ergeben sich nun
\(\begin{align} y_{\textrm{min}} &= y_2 - \frac{(a + b)^2}{8\cdot c}\\ &= 1.381222 - \frac{(-2.08\cdot 10^{-4} + 2.3\cdot 10^{-5})^2}{8\cdot 2.31\cdot 10^{-4}}\\ &= 1.381203 \end{align}\)
\(\begin{align} n_{\textrm{min}} &= - \frac{(a + b)}{2\cdot c}\\ &= - \frac{-2.08\cdot 10^{-4} + -2.3\cdot 10^{-5}}{2\cdot 2.31\cdot 10^{-4}}\\ &= 0\overset{d}{.}4004329 \end{align}\)
Die geringste Distanz von Mars zur Sonne ist also $\Delta = 1.381203\;AU$. Die dazugehörige Zeit findet man durch Multiplikation von vier Tagen (dem Tabellenintervall) mit dem Faktor $n_{\textrm{min}}$:
$0\overset{d}{.}4004329\cdot 4 = 1\overset{d}{.}60173$
Man erhält $1\overset{d}{.}60173$ Tage oder $1^d 14^h 26^m$ nach dem zentralen Wert, das ist dann der 17. Mai 1992, 14:26 $TD$.
Der exakte Wert laut JPL HORIZONS ist der 17. Mai 1992, 14:16 $TD$ mit der Entfernung $\Delta = 1.3812031008\;AU$
Beispiel 3
Von Merkur wurde die Deklination (geozentrisch) für März 2024 um jeweils 00:00 $TD$ berechnet (siehe Tabelle). Man berechne, wann die Deklination von Merkur $\delta = 0$ war.
Tabelle: Deklination vom Merkur im März 2024 um 00:00 $TD$ des jeweiligen Tages
| Zeitpunkt | Deklination [$^{\circ}$] |
|---|---|
| 10. März 2024, 00:00 $TD$ | $-0\overset{\circ}{.}637656572$ |
| 11. März 2024, 00:00 $TD$ | $0\overset{\circ}{.}286190911$ |
| 12. März 2024, 00:00 $TD$ | $1\overset{\circ}{.}210033028$ |
Aus der Tabelle sieht man, dass die Deklination vom 10. März zum 11. März das Vorzeichen wechselt.
Die Differenen 1. und 2. Ordnung sind
$a = y_2 - y_1 = 0.923847483$
$b = y_3 - y_2 = 0.923842117$
$c = y_1 + y_3 - 2\cdot y_2 = -5.336\cdot 10^{-6}$
Man startet mit $n_0 = 0$ und erhält
| \(\begin{align} n_0 &= \frac{-2\cdot y_2}{a + b + c\cdot 0}\\ & = \frac{-2\cdot 0.286190911}{0.923847483 + 0.923842117}\\ & = -0.30978245588436 \end{align}\) |
Dieser Wert wird rechts wieder eingesetzt und man erhält sukzessive die verbesserten Werte
$n_0 = -0.30978217718569$
$n_0 = -0.30978217718594$
$n_0 = -0.30978217718594$
Der Wert ändert sich nicht mehr, und der gesuchte Zeitpunkt ist daher um
$-0\overset{d}{.}3097822 = -0^d 7^h 26^m$ vor dem zentralen Wert (11. März), also am 10. März 2024 16:34 $TD$.
Interpolation mit fünf Tabellenwerten
Wenn Differenzen in 3. Ordnung nicht vernachlässigt werden dürfen, müssen mehr als drei Tabellenwerte benutzt werden. Mit fünf aufeinanderfolgenden Tabellenwerten $y_1$ bis $y_5$ bildet man, wie zuvor beschrieben, die Tabelle der Differenzen. Darin sind $a = y_2 - y_1$, $e = b - a$, $h = f - e$, usw.
Die gesamte Differenzentabelle lautet:
| Tabelle 2 | ||||
|---|---|---|---|---|
| $y$-Wert | Diff. 1. Ordnung | Diff. 2. Ordnung | Diff. 3. Ordnung | Diff. 4. Ordnung |
| $y_1$ | ||||
| $a = y_2 - y_1$ | ||||
| $y_2$ | $e = b - a$ | |||
| $-\uparrow$ | $b = y_3 - y_2$ | $h = f - e$ | ||
| $y_3$ | $f = c - b$ | $k = j - h$ | ||
| $+\downarrow$ | $c = y_4 - y_3$ | $j = g - f$ | ||
| $y_4$ | $g = d - c$ | |||
| $d = y_5 - y_4$ | ||||
| $y_5$ | ||||
Wieder ist $n$ der Interpolationsfaktor, gemessen vom zentralen Wert $y_3$, positiv in Richtung $y_4$ und negativ in Richtung $y_2$. Die Interpolationsformel lautet hier
| $$y = y_3 + \frac{n}{2}\cdot \big( b + c \big) + \frac{n^2}{2}\cdot f + \frac{n\cdot (n^2 - 1)}{12}\cdot \big( h + j \big) + \frac{n^2\cdot (n^2 - 1)}{24}\cdot k $$ |
Der Interpolationsfaktor $n_{\textrm{m}}$, der einem Extremum der Funktion entspricht, kann durch folgende Gleichung ermittelt werden:
| $$n_{\textrm{m}} = \frac{6\cdot b + 6\cdot c - h - j + 3\cdot n_{\textrm{m}}^2\cdot (h + j) + 2\cdot n_{\textrm{m}}^3\cdot k}{k - 12\cdot f}$$ |
Das ist wie zuvor durch Iteration möglich, indem man zuerst auf der rechten Seite $n_{\textrm{m}} = 0$ setzt. Wenn $n_{\textrm{m}}$ gefunden ist, kann der Wert in die darüber stehende Interpolationsformel eingesetzt werden.
Schließlich kann der Interpolationsfaktor $n_0$, der einer Nullstelle der Funktion entspricht, mit der Formel
| $$n_0 = \frac{-24\cdot y_3 + n_0^2\cdot (k - 12\cdot f) - 2\cdot n_0^3\cdot (h + j) - n_0^4\cdot k}{2\cdot (6\cdot b + 6\cdot c - h - j)}$$ |
berechnet werden, wobei $n_0$ wieder durch Iteration ermittelt wird, indem man mit $n_0 = 0$ auf der rechten Seite beginnt.
Es gilt wieder derselbe Grundsatz wie im Abschnitt „drei Tabellenwerte“: Wenn die Krümmung der Kurve im betrachteten Intervall bedeutend ist, muss folgende Methode zur Berechnung der Nullstelle $n_0$ verwendet werden. Man berechne
\[\begin{align} M &= \frac{k}{24}\\ N &= \frac{h + j}{12}\\ P &= \frac{f}{2} - M\\ Q &= \frac{b + c}{2} - N\\ \end{align}\]
Dann ist die Korrektur zum ersten angenommenen Wert von $n_0$ gegeben durch
| $$\Delta n_0 = \frac{M\cdot n_0^4 + N\cdot n_0^3 + P\cdot n_0^2 + Q\cdot n_0 + y_3}{4\cdot M\cdot n_0^3 + 3\cdot M\cdot n_0^2 + 2\cdot P\cdot n_0 + Q}$$ |
Auch hier muss die Rechnung wieder mit dem neuen Wert von $n_0$ solange wiederholt werden, bis sich $n_0$ nicht mehr ändert bzw. der Absolutwert der Änderung unter einem vorher festgelegten Wert liegt.
Beispiel 4
Man berechne die Horizontalparallaxe des Mondes aus den gegebenen Tabellenwerten für den 10. März 2024 um 16:20 $TD$.
| Zeitpunkt | Parallaxe |
|---|---|
| 09. März 2024, 12:00 $TD$ | $1^{\circ} 01' 19\overset{''}{.}95$ |
| 10. März 2024, 00:00 $TD$ | $1^{\circ} 01' 25\overset{''}{.}52$ |
| 10. März 2024, 12:00 $TD$ | $1^{\circ} 01' 25\overset{''}{.}94$ |
| 11. März 2024, 00:00 $TD$ | $1^{\circ} 01' 21\overset{''}{.}20$ |
| 11. März 2024, 12:00 $TD$ | $1^{\circ} 01' 11\overset{''}{.}46$ |
Die Tabelle gibt die Mondparallaxe im Abstand von 12 Stunden an. Zunächst sind die $y$-Werte in Grad/Bogenminuten/Bogensekunden gegeben, was nicht direkt verwendet werden kann. Man rechnet in Bogensekunden um und erhält die Tabelle
| Zeitpunkt | Parallaxe |
|---|---|
| 09. März 2024, 12:00 $TD$ | $3679\overset{''}{.}95$ |
| 10. März 2024, 00:00 $TD$ | $3685\overset{''}{.}52$ |
| 10. März 2024, 12:00 $TD$ | $3685\overset{''}{.}94$ |
| 11. März 2024, 00:00 $TD$ | $3681\overset{''}{.}20$ |
| 11. März 2024, 12:00 $TD$ | $3671\overset{''}{.}46$ |
Der gesuchte Zeitpunkt 16:20 ist um $4^h 20^m$ nach dem Zeitpunkt 10. März, 12:00 $TD$, demnach ist der Interpolationsfaktor
$n = \frac{4^h 20^m}{12^h} = \frac{4\overset{h}{.}333333}{12^h} = 0.361111\dots$.
Für die Werte $a, b, \dots k$ erhält man sukzessive
\(\begin{align} a &= 5.57\\ b &= 0.42\\ c &= -4.74\\ d &= -9.74\\ e &= -5.15\\ f &= -5.16\\ g &= -5.00\\ h &= -0.01\\ j &= 0.16\\ k &= 0.17\\ \end{align}\)
Eingesetzt in die Interpolationsformel ergibt das
$y = 3684\overset{''}{.}82$ am 10. März 2024 um 16:20 $TD$.
Den Zeitpunkt des Extremwerts – hier ein Maximum – erhält man durch Einsetzen in die Gleichung für $n_{\textrm{m}} = 0$ zunächst
\(\begin{align} n_{\textrm{m}} &= \frac{6\cdot b + 6\cdot c - h - j }{k - 12\cdot f}\\ &= -0.419874 \end{align}\)
Weitere Iterationen mit dem jeweils neuen Wert liefern
| \(\begin{align} n_{\textrm{m}} &= \frac{6\cdot 0.42 + 6\cdot (-4.74) - (-0.01) - 0.16 + 3\cdot (-0.419874)^2\cdot (-0.01 + 0.16) + 2\cdot (-0.419874)^3\cdot 0.17}{0.17 - 12\cdot (-5.16)}\\ &=-0.421728 \end{align}\) |
$\vdots\quad\vdots$
$-0.421746$
$-0.421746$
Nach 2 weiteren Iterationen ändert sich der Wert nicht mehr. In Einheiten des Tabellenintervalls hat man daher
$-0.421746\cdot 12^h = -5\overset{h}{.}06095 = -5^h 3^m 39^s$ vom Zentralwert $y_3$.
Das ist dann der Zeitpunkt 10 März 2024, 06:56:21 $TD$.
Den extremalen Wert selbst erhält man durch Einsetzen vom $n = n_{\textrm{m}}$ in die Interpolationsformel:
\(\begin{align} y_m &= y_3 + \frac{n_{\textrm{m}}}{2}\cdot \big( b + c \big) + \dots\\ &= 3686\overset{''}{.}40 \end{align}\)
Wichtige Hinweise
- Interpolation kann nicht direkt auf komplexe Größen angewendet werden. Diese Größen müssen erst in eine einzelne, brauchbare Größe umgewandelt werden. Zum Beispiel müssen Winkel, die in Grad, Minuten und Sekunden ausgedrückt sind, entweder in eine dezimale Gradzahl oder in Bogensekunden umgewandelt werden, bevor sie interpoliert werden können.
- Interpolieren von Zeiten und Rektaszensionen. Man bedenke, dass Zeiten und Rektaszensionen auf Null springen, wenn der Wert von 24 Stunden erreicht ist. Das muss berücksichtigt werden, wenn tabulierte Werte interpoliert werden.
- Man vermeide möglichst eine Interpolation für $\vert n\vert \gt 0.5$. Auf jeden Fall muss der Interpolationsfaktor $n$ in den Grenzen von $-1$ und $+1$ gehalten werden. Die gleiche Regel gilt für die Berechnung eines Extremums oder der Nullstelle einer Funktion. Man wählt als zentralen Wert von $y$ jenen Tabellenwert, der dem Extremum oder der Nullstelle am nächsten liegt. Natürlich kennt man den exakten Wert von $n_{\textrm{m}}$ oder $n_0$ nicht im Voraus. Erst muss ein genäherter Wert berechnet werden, wonach noch die Wahl des zentralen Wertes ($y_3$ oder $y_2$) zu ändern ist. Wenn der gewählte Wert zu weit von Null oder vom Extremum entfernt ist, würden die oben angegebenen Formeln inkorrekte oder sogar absurde Ergebnisse liefern!