Geozentrische Breite

Zur Bestimmung der topozentrischen Koordinaten (griech. $\tau\omicron\pi\omicron\varsigma$ Topos, Ort) eines Himmelkörpers benötigt man die geozentrischen Größen $\beta_0'$ und $\rho$. Dies ist meist nur für erdnahe Objekte wie z.B. den Mond notwendig, da der Mond eine relativ große Horizontalparallaxe von ca. $57'$ hat.

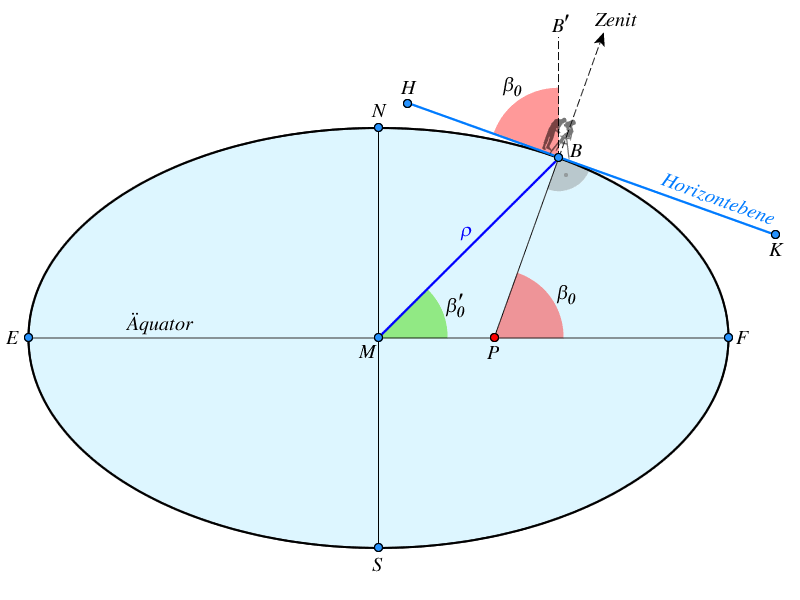
Abb.1 zeigt einen Meridianschnitt durch die Erde. Die Abplattung des Erdkörpers ist zu Anschauungszwecken extrem übertrieben dargestellt. $M$ ist der Erdmittelpunkt, $N$ und $S$ der Nord- bzw. Südpol. Die Verbindung $\overline{EF}$ stellt den Äquator dar, und $\overline{HK}$ ist die Horizontebene eines Beobachters $B$ auf der Erdoberfläche. Die Senkrechte zur Horizontebene in $B$ schneidet den Äquator im Punkt $P$.

Abb. 1

Die Verbindung $\overline{BB'}$ ist parallel zur Richtung $\overline{NS}$, und die geografische Breite $\beta_0$ taucht als Winkel $\beta_0 = \angle B'BH$ wiederum auf.

Zur Umrechnung von geozentrischen äquatorialen Koordinaten in die topozentrischen äquatorialen Koordinaten müssen $\beta_0'$ und $\rho$ berechnet werden. Dies kann man mit folgenden Näherungsformeln erreichen: (Siehe ⇒ O.Montenbruck, Grundlagen der Ephemeridenrechnung)

\[\tag{1}\label{1} \begin{align} \beta_0' &\approx \beta_0- 0\overset{\circ}{.}1924\cdot \sin(2\beta_0) \\ \rho &\approx R_E - 21.38\cdot \sin^2(\beta_0) \end{align} \]

Am Äquator und am Pol ist die Abweichung der geozentrischen Breite $\beta_0'$ von der geografischen Breite $\beta_0$ gleich $0$. Die größte Abweichung erhält man für $\beta_0 = 45^\circ$ mit etwa $0\overset{\circ}{.}192425 = 0^\circ 11' 32\overset{''}{.}7$.

Abb. 2

Nach Jean Meeus kann man die Größen $\beta_0'$ und $\rho$ auch mit den folgenden Näherungsformeln ermitteln. Zu beachten sind die Korrekturterme in Bogensekunden.

$$ \beta_0' \approx \beta_0 - 692\overset{''}{.}73\cdot \sin(2\cdot\beta_0) - 1\overset{''}{.}6\cdot \sin(4\cdot\beta_0) $$

und $\rho$ in Einheiten des Äquatorradius $R_E$

\[ \begin{align} \rho \approx\big{[}( & 0.9983271 \\ +&0.0016764\cdot \cos(2\cdot\beta_0) \\ -&0.0000035\cdot \cos(4\cdot\beta_0)\big{]}\cdot\ R_E \end{align} \]

Der geozentrische Abstand $\rho$ bezieht sich auf Meereshöhe, topografische Unebenheiten werden hier vernachlässigt.

Bei J. Meeus werden die Werte $\varrho$ mit dem Sinus bzw. dem Cosinus von $\beta_{0}'$ zu einer Größe zusammen gefasst berechnet. Dabei ist

• $\varrho$ = geozentrischer Abstand eines Beobachters auf der Erdoberfläche, in Einheiten des Erdradius $R_E$.
• $\beta_{0}'$ = geozentrische Breite des Beobachters.

Diese Größen $\varrho\sin\beta_{0}'$ bzw. $\varrho\cos\beta_{0}'$ werden für die Berechnung der topozentrischen Koordinaten für die Korrektur der Parallaxe benötigt, sowie auch bei der Berechnung von Finsternissen oder Bedeckungen. In den Astronomical Algorithms wird der nachstehende Algorithmus für ihre Berechnung angegeben.

Durch die Abplattung des Erdkörpers ändert sich die Breitenangabe ein wenig, es ist anstatt der geografischen Breite $\beta_{0}$ die geozentrische Breite $\beta_{0}'$ zu verwenden.

Ausgehend vom Äquatorradius der Erde mit

$$ R_E = 6378.14\,\textrm{km}$$

und der Abplattung $f$ der Erde mit

$$ f = \frac{R_E - R_P}{R_E} = \frac{1}{298.257} \approx 0.0033528132$$

erhält man den Polradius der Erde durch

$$ R_{P} = R_{E}\cdot(1 - f) = 6356.755\,\textrm{km}$$

Für einen Ort auf Meereshöhe kann man dann aus der geografischen Breite $\beta_{0}$ die geozentrische Breite $\beta_{0}'$ ermitteln durch

$$\beta_{0}' = \arctan\left( \frac{R_P^2}{R_E^2}\cdot \tan\beta_{0}\right)$$

Befindet sich der Beobachter auf der Höhe $H$ (in Meter) über dem Meeresspiegel, lassen sich die Größen $\varrho\sin\beta_{0}'$ und $\varrho\cos\beta_{0}'$ wie folgt berechnen:

\[\begin{align} \tan u &= \frac{R_P}{R_E}\cdot \tan\beta_{0}\quad\textsf{und damit}\\\\ \varrho\sin\beta_{0}' &= \frac{R_P}{R_E}\cdot\sin u + \frac{H}{6378140}\cdot\sin\beta_{0}\\\\ \varrho\cos\beta_{0}' &= \cos u + \frac{H}{6378140}\cdot\cos\beta_{0}\\ \end{align}\]

Dabei sind die Identitäten der Sinus- bzw. Tangensfunktion von Nutzen.

Die Größe $\varrho\sin\beta_{0}'$ ist in nördlichen Breiten positiv und in südlichen Breiten negativ, während der Wert von $\varrho\cos\beta_{0}'$ immer positiv ist. Wie man aus den Formeln erkennen kann, hat die geografische Länge $\lambda_{0}$ keinen Einfluss auf die Berechnung, sondern nur die geografische Breite $\beta_{0}$.