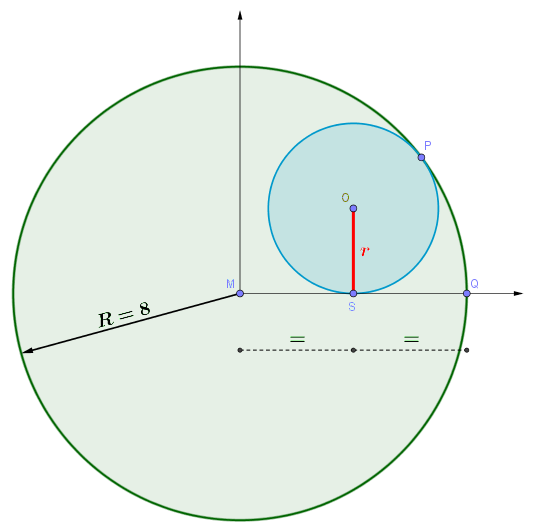
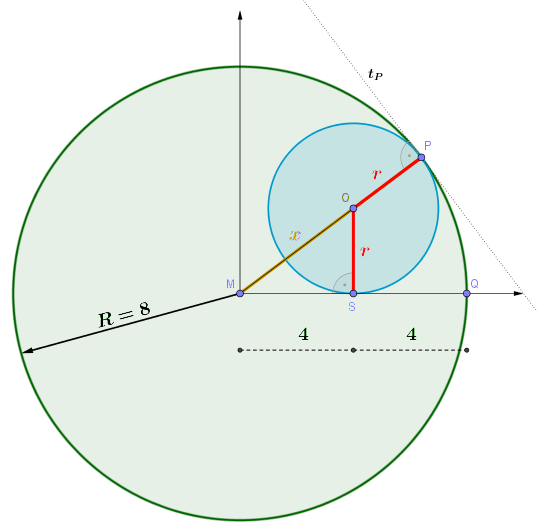
Gegeben: In einem Kreis mit dem Radius \(R=8\) befindet sich ein kleinerer Kreis, der den größeren im Punkt \(P\) berührt. Ein weiterer Berührpunkt \(S\) liegt auf der waagrechten Strecke \(\overline{MQ}\) und teilt diese in der Hälfte.
Gesucht: Radius \(r\) des kleineren Kreises (rot).
Die Strecke \(\overline{MQ}\) ist offensichtlich gleich dem Radius \(R=8\) des großen Kreises. Der Punkt \(S\) teilt diese Strecke in der Hälfte, also bei \(4\). Die Strecke \(\overline{OP}\) ist ebenfalls der Radius des kleinen Kreises. Da der Punkt \(P\) ein Berührpunkt der beiden Kreise ist, haben die beiden Kreise dort dieselbe Tangente \(t_P\). Die Tangente an einen Kreis steht immer senkrecht zum Radius, daher liegen die Punkte \(M,O,P\) auf einer Linie.
Es sei \(x\) die Strecke \(\overline{MO}\). Da die Strecke \(\overline{MP}=R\) ist, folgt
\(x = R-r = 8-r\)
Aus dem rechtwinkeligen Dreieck \(\triangle MSO\) berechnet sich \(x\) mit dem Satz des Pythagoras zu
\(4^2+r^2=x^2\)
Setzt man das zuvor erhaltene \(x = 8-r\) ein, ergibt sich
\(\displaystyle {{4}^{2}}+{{r}^{2}}={{\left( {8-r} \right)}^{2}}\)
Ausrechnen liefert
\(\displaystyle \begin{align}{}16+{{r}^{2}}&={{\left( {8-r} \right)}^{2}}\\16+\bcancel{{{{r}^{2}}}}&=64-2\cdot 8\cdot r+\bcancel{{{{r}^{2}}}}\\16&=64-16\,r\\16\,r&=48\\r&=3\end{align}\)
Der Radius des kleinen Kreises ist \(r = 3\).