Sinus, Cosinus und Tangens häufiger Winkel
Nachstehend wird gezeigt, wie man sich für häufig vorkommende Winkelwerte wie z.B. \(30^{\circ}, 45^{\circ}, 60^{\circ}\) die entsprechenden Sinus-, Cosinus- und Tangenswerte herleiten kann.
Beginnen wir mit dem Sinus von \(\displaystyle 30{}^\circ \).
Der \(\sin(30^{\circ})\) eignet sich sehr schön zur grafischen Darstellung am Einheitskreis.
Schritt 1
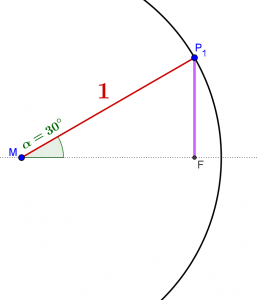
Man zeichnet sich einen Einheitskreis, Radius \(r=1\). Nun trägt man den Winkel \(\alpha=30^{\circ}\) nach oben hin auf und erhält den Schittpunkt \(P_1\). Der Fußpunkt \(F\) befindet sich senkrecht unterhalb von \(P_1\).
Die Strecke \(\displaystyle \overline{{{{P}_{1}}F}}\) ergibt sich aus
\(\displaystyle \frac{{GK}}{{HYP}}=\frac{{\overline{{{{P}_{1}}F}}}}{1}=\sin (30{}^\circ )\)
\(\displaystyle\sin (30{}^\circ )=\overline{{{{P}_{1}}F}}\)
Schritt 2
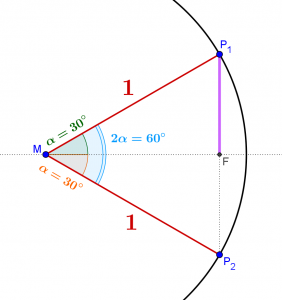
Um die Länge dieser Strecke zu ermitteln zeichnet man den Winkel \(\displaystyle \alpha \) noch einmal in die andere Richtung (nach unten) ein, man erhält am Kreis den Schnittpunkt \(\displaystyle {{P}_{2}}\). Am Mittelpunkt \(\displaystyle M\) ist nun der doppelte Winkel \(\displaystyle 2\alpha =60{}^\circ \) entstanden, den die beiden Kreisradien einschließen.
Da diese Schenkel die selbe Länge haben und einen Winkel von \(\displaystyle 60{}^\circ \) einschließen, kann man schließlich das gleichseitige Dreieck \(\displaystyle \triangle M{{P}_{1}}{{P}_{2}}\) einzeichnen.
Schritt 3
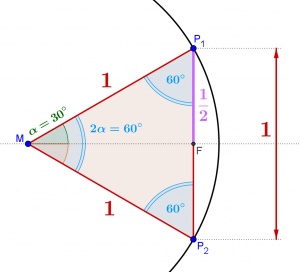
Da das Dreieck gleichseitig ist, muss die Strecke \(\displaystyle \overline{{{{P}_{1}}{{P}_{2}}}}\) ebenfalls die Länge \(1\) haben.
Das Dreieck ist symmetrisch zur \(x-\)Achse, der Fußpunkt \(F\) teilt also die Strecke \(\displaystyle \overline{{{{P}_{1}}{{P}_{2}}}}\) in der Hälfte. Daraus folgt
\(\displaystyle \overline{{{{P}_{1}}F}}=\frac{{\overline{{{{P}_{1}}{{P}_{2}}}}}}{2}=\frac{1}{2}\)
Der Sinuswert von \(\displaystyle 30{}^\circ \) muss also \(\displaystyle \sin (30{}^\circ )=\frac{1}{2}\) sein.
Nachdem wir den \(\displaystyle \sin (30{}^\circ )=\frac{1}{2}\) geometrisch bestimmt haben, können wir die anderen Werte aus den Zusammenhängen für \(sin, cos, tan\) herleiten.
cos(60°)
Aus dem Satz für Komplementärwinkel wissen wir, dass
\(\displaystyle \cos (90{}^\circ -\alpha )=\sin (\alpha )\) ist.
Wir kennen den \(\displaystyle \sin (30{}^\circ )=\frac{1}{2}\), daher folgt
\(\displaystyle \cos (90{}^\circ -30{}^\circ )=\sin (30{}^\circ )\)
\(\displaystyle =\frac{1}{2}\Rightarrow \cos (60{}^\circ )=\frac{1}{2}\)
cos(30°)
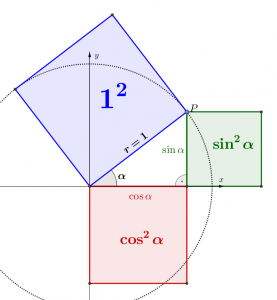
Trigonometrischer Pythagoras am Einheitskreis
Aus dem Einheitskreis kennen wir den Zusammenhang, den man „trigonometrischen Pythagoras“ nennt:
\(\displaystyle {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\)
Wir kennen den \(\displaystyle \sin (30{}^\circ )=\frac{1}{2}\), daher folgt
\(\displaystyle {{\cos }^{2}}(30{}^\circ )=1-{{\sin }^{2}}(30{}^\circ )=\)
\(\displaystyle =1-{{\left( {\frac{1}{2}} \right)}^{2}}=1-\frac{1}{4}=\frac{3}{4}\)
\(\displaystyle \cos (30{}^\circ )=\sqrt{{\frac{3}{4}}}=\frac{{\sqrt{3}}}{{\sqrt{4}}}=\)
\(\displaystyle =\frac{{\sqrt{3}}}{2}\approx 0,8660254….\)
tan(30°)
Der \(\displaystyle \tan (30{}^\circ )\) ergibt sich aus dem Zusammenhang
\(\displaystyle \tan \alpha =\frac{{\sin \alpha }}{{\cos \alpha }}\), wir haben also
\(\displaystyle \tan (30{}^\circ )=\frac{{\sin (30{}^\circ )}}{{\cos (30{}^\circ )}}=\)
\(\displaystyle =\frac{{\frac{1}{2}}}{{\frac{{\sqrt{3}}}{2}}}=\frac{{1\cdot 2}}{{2\cdot \sqrt{3}}}=\)
\(\displaystyle =\frac{1}{{\sqrt{3}}}\approx 0.57735…\)
sin(60°)
Hier kann man wieder den Komplementärwinkelsatz verwenden, es gilt
\(\displaystyle \sin (90{}^\circ -\alpha )=\cos (\alpha )\)
Wir kennen den \(\displaystyle \cos (30{}^\circ )=\frac{\sqrt{3}}{2}\), daher folgt
\(\displaystyle \sin (90{}^\circ -30{}^\circ )=\sin(60{}^\circ)=\)
\(\displaystyle =\cos (30{}^\circ )=\frac{\sqrt{3}}{2}\approx 0,8660254…\)
tan(60°)
Genau so wie zuvor berechnet sich der \(\displaystyle \tan (60{}^\circ )\) zu
\(\displaystyle \tan (60{}^\circ )=\frac{{\sin (60{}^\circ )}}{{\cos (60{}^\circ )}}=\frac{{\frac{{\sqrt{3}}}{2}}}{{\frac{1}{2}}}=\)
\(\displaystyle =\frac{{2\cdot \sqrt{3}}}{{1\cdot 2}}=\sqrt{3}\approx 1.73205…\)
sin(45°) & cos(45°)
Für \(\displaystyle \alpha =45{}^\circ \) sind im Einheitskreis beide Katheten gleich lang sind, man kann den \(\cos(\alpha)\) durch den \(\sin(\alpha)\) ersetzen (oder umgekehrt) und erhält
\(\displaystyle {{\sin }^{2}}(45{}^\circ)+{{\sin }^{2}}(45{}^\circ )=1\)
\(\displaystyle \Rightarrow 2\cdot {{\sin }^{2}}(45{}^\circ )=1\)
\(\Rightarrow \quad {{\sin }^{2}}(45{}^\circ )=\frac{1}{2}\)
\(\displaystyle \sin (45{}^\circ )=\sqrt{{\frac{1}{2}}}=\frac{1}{{\sqrt{2}}}=\)
\(\displaystyle =\frac{1}{{\sqrt{2}}}\cdot \frac{{\sqrt{2}}}{{\sqrt{2}}}=\)
\(\displaystyle =\frac{{\sqrt{2}}}{2}=\cos (45{}^\circ )\)
tan(45°)
Schließlich folgt noch aus
\(\displaystyle \tan \alpha =\frac{{\sin \alpha }}{{\cos \alpha }}\)
\(\displaystyle \tan (45{}^\circ )=\frac{{\sin (45{}^\circ )}}{{\cos (45{}^\circ )}}=\frac{{\frac{{\sqrt{2}}}{2}}}{{\frac{{\sqrt{2}}}{2}}}=1\)
Wir haben nun alle wichtigen Werte im \(I.\, Quadranten\) hergeleitet.
| Winkel |
sin |
cos |
tan |
| 30° |
\(\frac{1}{2}\) |
\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{\sqrt{3}}\) |
| 45° |
\(\frac{\sqrt{2}}{2}\) |
\(\frac{\sqrt{2}}{2}\) |
\(1\) |
| 60° |
\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{2}\) |
\(\sqrt{3}\) |
Die entsprechenden Werte in den anderen Quadranten ergeben sich durch Symmetrie und dem Komplenmentär- bzw. Supplementärwinkelsatz. Eine Tabelle mit wichtigsten Winkeln kann hier heruntergeladen werden.