Die sogenannten „Linearen Gleichungen“ mit einer Variablen sind von der Form

\(\displaystyle \large{a\cdot x+b=0}\)

Dabei sind \(\displaystyle a\) und \(\displaystyle b\) irgendwelche reellen Zahlen mit \(\displaystyle a,b\,\in \mathbb{R}\), wobei \(\displaystyle a\) nicht Null sein darf: \(\displaystyle a\ne 0\)

Das \(\displaystyle x\) ist die Variable, und jede Zahl \(\displaystyle x\), die diese Gleichung erfüllt, heißt Lösung der Gleichung.

Man sieht, dass die Lösung der Gleichung wie folgt aussieht:

\(\displaystyle \begin{align}a\cdot x+b & =0\quad \quad |-b\\a\cdot x & =-b\quad \,\,|:a\\x & =-\frac{b}{a}\end{align}\)

Eine lineare Gleichung \(\displaystyle a\cdot x+b=0\) mit \(\displaystyle a\ne 0\) besitzt immer eine Lösung, nämlich \(\displaystyle x=-\frac{b}{a}\)

Merkmal einer linearen Gleichung ist, dass die Variable \(\displaystyle x\) nur als \(\displaystyle x\) selbst vorkommt, und nicht mit einer Potenz wie z.B. \(\displaystyle x^2\) oder \(\displaystyle x^3\) usw.

Wenn man die Gleichung als Graph darstellt, also verschiedene Werte für \(\displaystyle x\) einsetzt, erhält man eine Gerade.

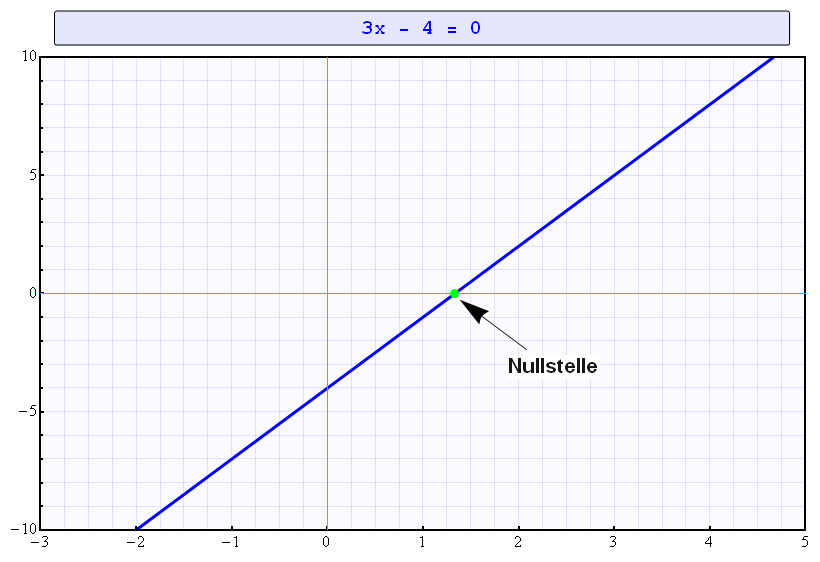Hier ist das am Beispiel \(a=3,\;b=-4\) dargestellt, also die Gleichung \(\displaystyle 3\cdot x-4=0\).

Die Gleichung für \(\displaystyle x\) zu lösen bedeutet, man sucht den Punkt, an der die Gerade die x-Achse schneidet. Dort ist der y-Wert gleich Null, es ist eine sogenannte Nullstelle. In diesem Fall liegt die Nullstelle bei

\(\displaystyle \begin{align}3x-4 & =0\quad \quad |+4\\3x & =4\quad \quad |:3\\x & =\frac{4}{3}\end{align}\)