Das Integral

Die Berechnung „Integrieren“ bedeutet nichts Anderes als die Umkehrung des Ableitens. Man könnte sagen, man sucht jene Funktion \(F(x)\), die abgeleitet die gegebene Funktion \(f(x)\) ergibt.

Wir wissen z.B., das die Ableitung von \(f(x)=x^2 \Rightarrow f'(x)=2x\) ist. D.h., wenn man zu diesen \(2x\) jene Funktion sucht, die eben abgeleitet werden muss, um \(2x\) zu ergeben, dann integriert man. Man nennt diese Funktion Stammfunktion und bezeichnet sie mit einem großen \(F\).

Es gilt:
\(F'(x) = f(x)\) bzw.
\(\int {f(x)\,{\mathrm{d}}x = F(x)} \)

Man schreibt ein Integral wie folgt:

\(\large {\underbrace {\int}_{Integralzeichen} \underbrace {2x}_{Integrand}\quad \underbrace {\mathrm{d}x}_{Infinitesimal}}\)

• Das Integralzeichen ist ein „langgezogenes S“, das rührt von der Bedeutung „Summe“ her. Es wird beim Integrieren etwas „aufsummiert“.
• Der „Integrand“ steht innen, das ist die Funktion, deren Stammfunktion man durch die Berechnung finden will.
• Hinten dran steht ein „Infinitesimal“ mit jener Variablen, „nach der“ integriert werden soll. Das Infinitesimal ist sozusagen ein „unendlich kleines Stück“ der Variable. Wenn z.B. \(x\) den Weg bezeichnet, ist \(\mathrm{d}x\) ein „unendlich kleines Wegstück“, oder wenn \(t\) die Zeit bezeichnet, ist \(\mathrm{d}t\) eine „unendlich kleine Zeitspanne“, usw.

Bestimmtes Integral

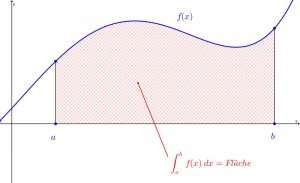Anschaullich macht man beim Integrieren nichts Anderes, als eine Fläche zu berechnen (bzw. ein Volumen in 3 Dimensionen), nämlich die Fläche unter der gegebenen Funktion, gemessen bis zur x-Achse. Das nebenstehende Bild zeigt ein Integral unter der Funktion \(f(x)\) mit den Integral-Grenzen \(a\) und \(b\). Genau genommen ist das ein sogenanntes bestimmtes Integral, weil die Integralgrenzen gegeben sind und man genau „von \(a\) bis \(b\)“ integriert.

Unbestimmtes Integral

Es gibt aber auch das unbestimmte Integral, bei dem man ganz allgemein die Stammfunktion zu einer gegebenen Funktion berechnet, ohne bestimmte Grenzen zu haben. Betrachtet man das obige Beispiel mit

\(f(x) = 2x\), dann ergibt sich als Stammfunktion

\(\int f(x) \mathrm{d}x = \int 2x \mathrm{d}x = x^2 + C\)

Plus was?
Plus „C“, eine beliebige Konstante (die nicht von \(x\) abhängt)! Vom Ableiten her wissen wir, dass konstante Werte wegfallen, weil deren Ableitung = 0 ist. Wenn man eine Funktion integriert, taucht diese Integrationskonstante \(C\) wieder auf. Die Stammfunktion ist also nicht eindeutig, weil man immer eine beliebige Konstante dazu nehmen kann. Das unbestimmte Integral ermittelt also „nur“ die Stammfunktion der gegebenen Funktion, und berechnet keinen konkreten Wert (Fläche, Volumen…).