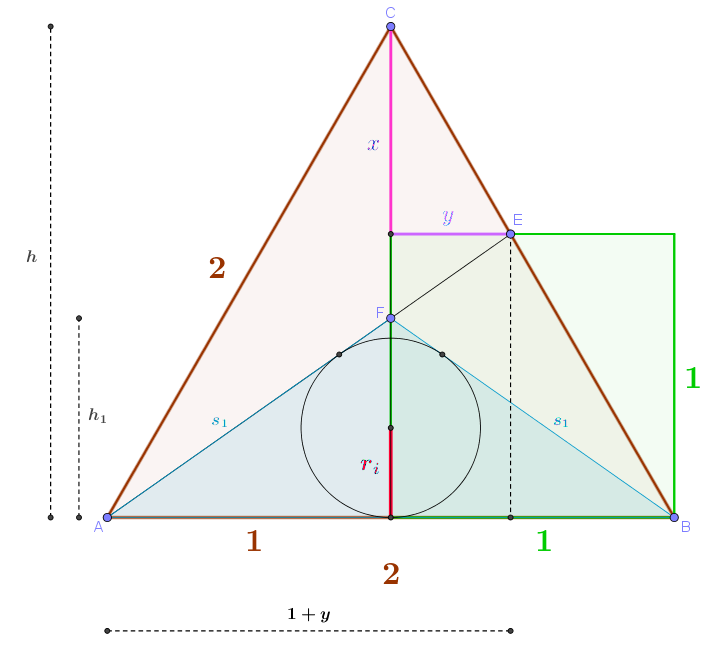
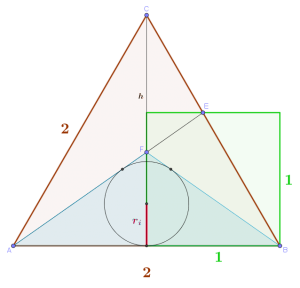
Gegeben: Ein gleichseitiges Dreieck \(\triangle ABC\) mit der Seitenlänge \(s=2\), mit einem Quadrat bei Punkt \(B\) mit der Seitenlänge \(1\). Die obere Seite des Quadrats schneidet die Seite \(BC\) im Punkt \(E\), die Verbindung \(AE\) schneidet die Höhe \(h\) des Dreiecks im Punkt \(F\).
Gesucht: Der Inkreisradius \(r_i\) des Dreiecks \(\triangle ABF\) (in der Skizze rot).
Anmerkung: Die Aufgabe lässt sich komplett ohne Winkelberechnungen lösen! Es reichen der Satz von Pythagoras sowie die Kenntnis über ähnliche Dreiecke.
Hilfestellung: Der Inkreisradius eines Dreiecks ist gegeben durch \(\displaystyle {{r}_{i}}=\frac{{2A}}{U}\)
Die Höhe \(h\) des gleichseitigen Dreiecks \(\triangle ABC\) ist gegeben durch
\(\displaystyle \begin{align}{}{{1}^{2}}+{{h}^{2}}&={{2}^{2}}\quad \Rightarrow \\h&=\sqrt{{{{2}^{2}}-{{1}^{2}}}}=\sqrt{3}\end{align}\)
Die Länge \(x\) ist dann die Höhe \(h\) des Dreiecks abzüglich der Seitenlänge des Quadrats, also
\(x=h-1=\sqrt{3}-1\)
Nun verhält sich \(\displaystyle \frac{y}{x}\) so wie \(\displaystyle \frac{1}{h}\), also
\(\displaystyle y=\frac{x}{h}=\frac{{\sqrt{3}-1}}{{\sqrt{3}}}=1-\frac{1}{{\sqrt{3}}}\)
Jetzt zum gesuchten Dreieck \(\triangle ABF\):
Der Punkt \(E\) hat vom Punkt \(A\) die waagrechte Entfernung \(1+y\). Es verhält sich die Höhe des Quadrats \(1\) zu \((1+y)\) so wie die Höhe \(h_1\) des Dreiecks \(\triangle ABF\) zu \(1\), also
\(\displaystyle \frac{1}{{1+y}}=\frac{{{{h}_{1}}}}{1}\quad \Rightarrow \quad {{h}_{1}}=\frac{1}{{1+y}}\)
Einsetzen von \(\displaystyle y\) liefert
\(\displaystyle \begin{align}{}{{h}_{1}}&=\frac{1}{{1+\left( {1-\frac{1}{{\sqrt{3}}}} \right)}}\\&=\frac{1}{{2-\frac{1}{{\sqrt{3}}}}}=\frac{1}{{\frac{{2\sqrt{3}-1}}{{\sqrt{3}}}}}\\&=\frac{{\sqrt{3}}}{{2\sqrt{3}-1}}\end{align}\)
Rationalmachen des Nenners ergibt dann
\(\displaystyle \begin{align}{}{{h}_{1}}&=\frac{{\sqrt{3}}}{{2 \sqrt{3}-1}}\cdot \frac{{2\sqrt{3}+1}}{{2\sqrt{3}+1}}\\&=\frac{{\sqrt{3}\left( {2\sqrt{3}+1} \right)}}{{{{{\left( {2\sqrt{3}} \right)}}^{2}}-{{1}^{2}}}}\\&=\frac{{2\cdot 3+\sqrt{3}}}{{4\cdot 3-1}}\\&=\frac{{6+\sqrt{3}}}{{11}}\end{align}\)
Das gesuchte Dreieck \(\triangle ABF\) ist gleichschenkelig, und die beiden oberen Seiten \(s_1\) haben die Länge
\(\displaystyle {{s}_{1}}=\sqrt{{{{1}^{2}}+h_{1}^{2}}}=\sqrt{{1+h_{1}^{2}}}\)
Der Umfang des blauen Dreiecks ist daher
\(\displaystyle U=2+2\cdot {{s}_{1}}=2+2\cdot \sqrt{{1+h_{1}^{2}}}\)
und die Fläche ist
\(\displaystyle A=2\cdot \left( {\frac{{{{h}_{1}}\cdot 1}}{2}} \right)={{h}_{1}}\)
Der Inkreisradius eines Dreiecks ist gegeben durch
\(\displaystyle \begin{align}{}{{r}_{i}}&=\frac{{2A}}{U}\\&=\frac{{2\,{{h}_{1}}}}{{2+2\cdot \sqrt{{1+h_{1}^{2}}}}}\\&=\frac{{2\,{{h}_{1}}}}{{2\cdot \left( {1+\sqrt{{1+h_{1}^{2}}}} \right)}}\\&=\frac{{{{h}_{1}}}}{{1+\sqrt{{1+h_{1}^{2}}}}}\end{align}\)
Man kann jetzt noch die Höhe \(\displaystyle {{h}_{1}}=\frac{{6+\sqrt{3}}}{{11}}\) einsetzen und erhält nach längerer Rechnung
\(\displaystyle \begin{align}{}{{r}_{i}}&=\frac{{\frac{{6+\sqrt{3}}}{{11}}}}{{1+\sqrt{{1+{{{\left( {\frac{{6+\sqrt{3}}}{{11}}} \right)}}^{2}}}}}}\\&=\frac{{6+\sqrt{3}}}{{11+11\cdot \sqrt{{1+\frac{{36+12\sqrt{3}+3}}{{121}}}}}}\\&=\frac{{6+\sqrt{3}}}{{11+11\cdot \sqrt{{\frac{{121}}{{121}}+\frac{{39+12\sqrt{3}}}{{121}}}}}}\\&=\frac{{6+\sqrt{3}}}{{11+11\cdot \sqrt{{\frac{{160+12\sqrt{3}}}{{121}}}}}}\\&=\frac{{6+\sqrt{3}}}{{11+11\cdot \frac{1}{{11}}\sqrt{{160+12\sqrt{3}}}}}\\&=\frac{{6+\sqrt{3}}}{{11+\sqrt{{4\cdot \left( {40+3\sqrt{3}} \right)}}}}\\&=\frac{{6+\sqrt{3}}}{{11+2\sqrt{{40+3\sqrt{3}}}}}\end{align}\)
Dieser Ausdruck ergibt dann für den Inkreisradius
\(\displaystyle {{r}_{i}}\approx 0,3163\)