Manchmal kann bzw. muss man quadratische Funktionen „faktorisieren“. Was bedeutet das?
Da heißt man stellt die Frage: „Kann man diese Funktion als Produkt zweier Klammern schreiben?„, in der Form
\(\definecolor{red}{RGB}{255,0,0} \) \((x\pm…) \cdot (x\pm…)\) ?
Diese Bererchnung wird auch als Linearfaktor-Zerlegung bezeichnet. Durch diese bekommt man auch die Nullstellen der Funktion.
Wir erinnern uns, dass die allgemeine Form der quadratischen Funktion \(f(x) = a x^2 + b x +c\) ist.
Der „einfache“ Fall: \(a=1\)
Hier steht vor dem \(x^2\) nur der Faktor 1, wir haben also eine Funktion in der Form
\(f(x) = x^2 + b x +c\) gegeben.
Die Lösung besteht darin, dass man die Zahl \(c\) in eine Multiplikation aus zwei Zahlen zerlegt, deren Summe dann den Wert der Zahl \(b\) ergeben muss. Am besten sieht man die Vorgehensweise an einem Beispiel:
\(f(x)=x^2 + 5x+6\)
\(b=5,\, c=6\)
Man nimmt den Wert \(c = 6\) und zerlegt ihn in eine Multiplikation. Wir haben in diesem Fall vier Möglichkeiten:
\(6 = 1 \cdot 6\)
\(6 = (-1) \cdot (-6)\)
\(6 = 2 \cdot 3\)
\(6 = (-2) \cdot (-3)\)
Wir haben die 6 in zwei Faktoren zerlegt. Nun sehen wir nach, welche Lösung in Summe die Zahl \(b=5\) ergibt:
\(1 + 6=7\)
\(-1+(-6)=-7\)
\(\color{red}{2 + 3=5}\)
\(-2+(-3)=-5\)
Der dritte Fall trifft zu, also sind unsere Faktoren hier die „+2“ und die „+3“, weil sie in Summe die „5“ (= b) ergeben. Daher können wir die Funktion faktorisiert schreiben als
\(f(x) = (x+2) \cdot (x+3)\)
Probe: Wenn wir das ausmultiplizieren, erhalten wir
\(f(x) = (x+2) \cdot (x+3) = x\cdot x + 2\cdot x + 3\cdot x + 2\cdot 3 = \underline{x^2 + 5x + 6}\) , also wieder unsere gegebene Funktion!
\(f(x)=x^2 – 1\cdot x -12\)
\(b=-1,\, c=-12\)
Wir müssen hier \(c=-12\) faktorisieren, es gibt in diesem Fall insgesamt sechs Möglichkeiten:
\(-12 = (-1) \cdot 12\)
\(-12 = 1 \cdot (-12)\)
\(-12 = (-2) \cdot 6\)
\(-12 = 2 \cdot (-6)\)
\(-12 =(-3) \cdot 4\)
\(\color{red}{-12 = 3 \cdot (-4)}\)
In Summe müssen die Faktoren die Zahl \(b=-1\) ergeben, das trifft nur bei „3“ und „-4“ zu, da \(3+(-4) = 3-4=-1\) ist. Also sind unsere Faktoren in diesem Fall \(3\) und \(-4\)
\(f(x) = (x+3) \cdot (x-4)\)
Probe: Wenn wir das ausmultiplizieren, erhalten wir wieder die gegebene Fuktion:
\(f(x) = (x+3) \cdot (x-4) = x\cdot x + 3\cdot x – 4\cdot x + 3\cdot (-4) = \underline{x^2 – x – 12}\)
Der „schwierige“ Fall: \(a\neq1\)
Wenn der Faktor \(a\) vor dem \(x^2\) nicht =1 ist, müssen wir anders vorgehen. Wir multiplizieren zuerst \(a\) mit \(c\) und zerlegen dann den erhaltenen Wert in eine Multiplikation. Diese beiden Faktoren müssen dann wieder in Summe die Zahl \(b\) ergeben! Damit haben wir jetzt unsere Faktoren ermittelt.
Dann schreiben wir eine Tabelle in der folgenden Art hin:
| \(a\cdot x^2\) | 1.Faktor \(\cdot x\) |
| 2.Faktor \(\cdot x\) | \(c\) |
Das weitere Vorgehen wird in den Beispielen erläutert.
\(f(x)=2x^2 + 1\cdot x -6\)
\(a=2,\, b=1,\, c=-6\)
Wir berechnen \(a \cdot c = 2\cdot (-6) = -12\) . Diese Zahl müssen wir jetzt faktorisieren. Es gibt (wie schon in Beispiel 2 berechnet) sechs Möglichkeiten:
\(-12 = (-1) \cdot 12\)
\(-12 = 1 \cdot (-12)\)
\(-12 = (-2) \cdot 6\)
\(-12 = 2 \cdot (-6)\)
\(\color{red}{-12 =(-3) \cdot 4}\)
\(-12 = 3 \cdot (-4)\)
In Summe müssen die Faktoren die Zahl \(b=1\) ergeben, das trifft nur bei „-3“ und „4“ zu, da \((-3)+4 = 1\) ist. Also sind unsere Faktoren hier \(-3\) und \(4\)
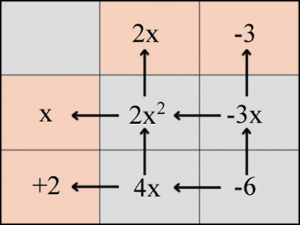
Wir schreiben unsere Tabelle hin wie oben angegeben
| \(2x^2\) | \(-3x\) |
| \(4x\) | \(-6\) |
Jetzt berechnen wir pro Zeile und pro Spalte die gemeinsamen Faktoren
1. Zeile: der gemeinsame Faktor von \(2x^2\) und \(-3x\) ist \(x\), links daneben hinschreiben.
2. Zeile: der gemeinsame Faktor von \(4x\) und \(-6\) ist \(2\), links daneben hinschreiben.
1. Spalte: der gemeinsame Faktor von \(2x^2\) und \(4x\) ist \(2x\), darüber hinschreiben.
2. Spalte: der gemeinsame Faktor von \(-3x\) und \(-6\) ist \(-3\), darüber hinschreiben.
Achtung! Die Vorzeichen der gemeinsamen Faktoren erhalten wir durch das Vorzeichen jenes Faktors, der den farbigen Zellen als nächstes steht.
Das \(x\) links ist positiv, weil es dem \(2x^2\) näher steht als dem \(-3x\).
Die \(+2\) links ist positiv, weil sie dem \(4x\) näher steht als der \(-6\).
| \(2x\) | \(-3\) | |
| \(x\) | \(2x^2\) | \(-3x\) |
| \(+2\) | \(4x\) | \(-6\) |
Wir sind fertig! Die Faktorisierung kann direkt abgelesen werden aus der farbigen Reihe bzw. Spalte:
\(f(x) = (2x-3) \cdot (x+2)\)
Probe: Wenn wir das ausmultiplizieren, erhalten wir wieder die gegebene Fuktion:
\(f(x) = (2x-3) \cdot (x+2) = 2x^2 – 3x + 4x – 6 = \underline{2x^2 + x -6}\)
\(f(x)=4x^2 -19x +12\)
\(a=4,\, b=-19,\, c=12\)
Wir berechnen \(a \cdot c = 4\cdot 12 = 48\) . Diese Zahl müssen wir jetzt faktorisieren. Es gibt hier acht (!) Möglichkeiten:
\(48 = 1 \cdot 48\)
\(48 = (-1) \cdot (-48)\)
\(48 = 2\cdot 24\)
\(48 = (-2)\cdot (-24)\)
\(48 = 3\cdot 16\)
\(\color{red}{48 = (-3)\cdot (-16)}\)
\(48 = 8\cdot 6\)
\(48 = (-8)\cdot (-6)\)
In Summe müssen die Faktoren die Zahl \(b=-19\) ergeben, das trifft nur bei „-3“ und „-16“ zu, da \((-3)+(-16) = -3-16 = -19\) ist. Also sind unsere Faktoren hier \(-3\) und \(-16\)
Wir schreiben unsere Tabelle hin
| \(4x^2\) | \(-3x\) |
| \(-16x\) | \(+12\) |
Gemeinsame Faktoren berechnen:
1. Zeile: der gemeinsame Faktor von \(4x^2\) und \(-3x\) ist \(x\), links daneben hinschreiben.
2. Zeile: der gemeinsame Faktor von \(-16x\) und \(+12\) ist \(-4\), links daneben hinschreiben.
1. Spalte: der gemeinsame Faktor von \(4x^2\) und \(-16x\) ist \(4x\), darüber hinschreiben.
2. Spalte: der gemeinsame Faktor von \(-3x\) und \(+12\) ist \(-3\), darüber hinschreiben.
Vorzeichen:
Das \(x\) links ist positiv, weil es dem \(4x^2\) näher steht als dem \(-3x\).
Die \(-4\) links ist negativ, weil sie dem \(-16x\) näher steht als der \(+12\).
Das \(4x\) oben links ist positiv, weil es dem \(4x^2\) näher steht als dem \(-16x\).
Die \(3\) oben rechts ist negativ, weil sie dem \(-3x\) näher steht als der \(+12\).
| \(4x\) | \(-3\) | |
| \(x\) | \(4x^2\) | \(-3x\) |
| \(-4\) | \(-16x\) | \(+12\) |
Wir sind fertig! Die Faktorisierung kann direkt abgelesen werden aus der farbige Reihen bzw. Spalte:
\(f(x) = (4x-3)\cdot (x-4)\)
Probe: Wenn wir das ausmultiplizieren, erhalten wir wieder die gegebene Fuktion:
\(f(x) = (4x-3)\cdot (x-4)= 4x^2 – 3x – 16x +12 = \underline{4x^2 -19x +12}\)
Achtung!
Man muss unbedingt vorher einen eventuell gemeinsamen Faktor aus der gegebenen Funktion herausziehen, sonst erhält man ein falsches Ergebnis!
Z.B. die Funktion \(f(x) = 2x^2 – 4x -16\)
Hier sieht man, dass der Faktor \(2\) in allen Termen enthalten ist, also kann man ihn ausklammern:
\(f(x) = 2x^2 – 4x -16 = 2\cdot(x^2-2x-8)\)
Jetzt faktorisiert man die in Klammer gegebene Funktion, und das Ergebnis wird mit dem ausgeklammerten Faktor \(2\) multipliziert. Außerdem ist hier durch das Ausklammern der 2 die Faktorisierung einfacher geworden, weil man nur den „einfachen“ Fall zu berechnen hat.
\(b=-2, c=-8\)
\(-8 = (-1)\cdot 8\)
\(-8 = 1\cdot (-8)\)
\(-8 = (-2)\cdot 4\)
\(-8 = \color{red}{2\cdot (-4)}\)
Die Faktoren sind \(2\) und \(-4\), da \(2+(-4)=-2 =b \) ist. Für die Lösung den zuvor ausgeklammerten Wert nicht vergessen!
\(f(x) = 2\cdot(x^2-2x-8) = \underline{2(x+2)(x-4)}\)