Ein bestimmtes Integral heißt so, weil es zwischen zwei vorgegebenen Grenzwerten berechnet wird. Das unbestimmte Integral hat ja keine Integrationsgrenzen, es wird nur die allgemeine Stammfunktion ermittelt. Beim bestimmten Integral wird eine Fläche unter der Funktion berechnet (oder ein Volumen in 3 Dimensionen), und zwar zwischen den vorgegebenen (Integral-)Grenzen, der Untergrenze und der Obergrenze.
Die Untergrenze beim bestimmten Integral schreibt man unter das Integralsymbol, und die Obergrenze entsprechend oberhalb:
\(\large{\int\limits^{Obergrenze}_{Untergrenze} (Integrand) \; dx}\)
Beim bestimmten Integral fällt auch die Integrationskonstante \(C \) weg, weil wir ja nach dem Integrieren die Werte für die Untergrenze bzw. Obergrenze einsetzen können und einen konkreten Wert ausrechnen. Wir integrieren die Funktion sozusagen “von…bis”. Das \(x\) im \(dx\) kann auch durch eine andere Variable ersetzt sein, je nachdem, nach welcher Variable integriert wird, z.B. nach der Zeit \(dt\) oder einem Winkel \(d\varphi\) usw.
Wenn man das Integral gelöst (also die Stammfunktion \(F\) des Integranden gefunden) hat, schreibt man diese in eckigen Klammern an und setzt nach der rechten Klammer die Integrationsgrenzen:
\(\int\limits^{Obergrenze}_{Untergrenze} (Integrand) \; dx = \left[Stammfunktion \right]\,_{Untergrenze}^{Obergrenze}\)
Jetzt setzt man die Grenzen in die gefundene Stammfunktion \(F\) ein, wobei man rechnet
\(F(Obergrenze) – F(Untergrenze)\)
Z.B.: Wenn die Stammfunktion mit \(x^2\) ermittelt wurde und das Integral die Grenzen von 1 und 4 hat
\(\displaystyle \left[ {{{x}^{2}}} \right]_{1}^{4}=\left( {{{4}^{2}}-{{1}^{2}}} \right)=16-1=15\)
Das Ergebnis ist dann die Lösung des bestimmten Integrals.
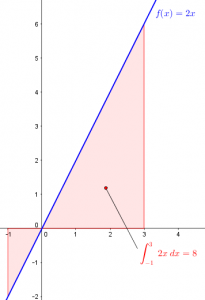Von den Ableitungen her wissen wir, dass \(f(x) = x^2\) abgeleitet \(f'(x) = 2x\) ist. Also ist die Stammfunktion \(F(x) = x^2\). Einsetzen der Integrationsgrenzen ergibt
\(\int\limits^3_{-1} 2x dx = [x^2]_{-1}^{+3} = [3^2 – (-1)^2] = 9 – 1 = 8\)
Die Fläche unter der Funktion \(f(x) = 2x\) von \(-1\) bis \(3\) ist also \(= 8\).
Zu beachten ist, das jene Teile der Fläche, die unterhalb der x-Achse liegen beim Integrieren als negativ gerechnet wird! Die Fläche ist hier offensichtlich
\(\frac{6\cdot 3}{2} – \frac{1\cdot 2}{2} = 9 – 1 = 8\)
Bei so einer einfachen Funktion (Gerade) hätte man nicht integrieren müssen.
\(e\) ist die Euler’scher Zahl = 2.71828182845….
Am Taschenrechner: [1] [2nd] \(e^{x}\) oder [2nd] \(e\) [ENTER]
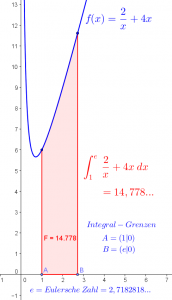
Zuerst müssen wir feststellen, wo das Integral eigentlich definiert ist und wo nicht. Der erste Integrand lautet \(\frac{2}{x}\), ist also bei \(x=0\) nicht definiert bzw. hat dort eine sogenannte Polstelle (durch die 0 darf nicht dividiert werden!). Über solche Polstellen darf nicht hinweg integriert werden. Da aber die Integrationsgranzen in diesem Beispiel von 1 bis \(e\) gehen, macht das keine Probleme. Der zweite Term \(4x\) macht auch keine Probleme.
Der Integrand besteht hier aus einer Summe von zwei Termen \(\frac{2}{x}\) und \(4x \), man kann das also in zwei Integrale aufteilen:
\(\int\limits^e_1\left(\frac{2}{x}+4x\right)dx = \int\limits^e_1\frac{2}{x}dx + \int\limits^e_1 4x dx\)
Die konstanten Faktoren dürfen vor das Integral herausgezogen werden:
\(2\cdot \int\limits^e_1\frac{1}{x}dx +4\cdot \int\limits^e_1 x dx\)
Jetzt haben wird zwei → Standard-Integrale, von denen wir die Lösungen kennen.
\(\int \frac{1}{x}dx = \ln{x} + C\) und \(\int xdx = \frac{x^2}{2} + C\)
(Das C brauchen wir hier nicht, wir haben ja unsere Integrationsgrenzen.)
Wir setzen ein und schreiben
\(2\cdot\left[\ln{x} \right]_1^e + 4\cdot \left[\frac{x^2}{2} \right]_1^e\)
Jetzt rechnet man aus, setzt also in die berechneten Stammfunktionen jeweils \(\it{Obergrenze – Untergrenze}\) ein, daher
\(2 \left[\ln{e}-\ln{1} \right] + 4 \left[\frac{e^2}{2} – \frac{1^2}{2} \right]\)
Wir wissen, dass \(\ln{e} = 1\) und \(\ln{1} = 0\) ist, daher erhalten wir
\(2 \left[1-0 \right] + 4 \left[\frac{e^2}{2} – \frac{1}{2} \right]\)
\(2 + \frac{4e^2}{2} – \frac{4}{2} = 2 + 2e^2 – 2 = \underline{2e^2} \approx 14.7781…\)